Fractional Taylor Monomials - Nabla Fractional Calculus - Discrete Fractional Calculus

Discrete Fractional Calculus (2015)

3. Nabla Fractional Calculus

3.11. Fractional Taylor Monomials

To find the formula for the Laplace transform of a fractional nabla Taylor monomial we will use the following lemma which appears in Hein et al [119].

Lemma 3.73.

For $$\nu \in \mathbb{C}\setminus \mathbb{Z}$$ and n ≥ 0, we have that

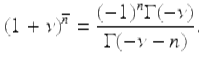
$$\displaystyle{ (1+\nu )^{\overline{n}} = \frac{(-1)^{n}\Gamma (-\nu )} {\Gamma (-\nu - n)}. }$$

(3.37)

Proof.

The proof of (3.37) is by induction for $$n \in \mathbb{N}_{0}$$ . For n = 0 (3.37) clearly holds. Assume (3.37) is true for some fixed n ≥ 0. Then,

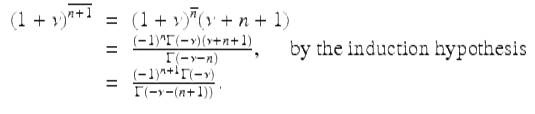
$$\displaystyle\begin{array}{rcl} (1+\nu )^{\overline{n + 1}}& =& (1+\nu )^{\overline{n}}(\nu +n + 1) {}\\ & =& \frac{(-1)^{n}\Gamma (-\nu )(\nu +n + 1)} {\Gamma (-\nu - n)},\quad \mbox{ by the induction hypothesis} {}\\ & =& \frac{(-1)^{n+1}\Gamma (-\nu )} {\Gamma (-\nu - (n + 1))}. {}\\ \end{array}$$

The result follows. □ 

We now determine the Laplace transform of the fractional nabla Taylor monomial.

Theorem 3.74.

For ν not an integer, we have that

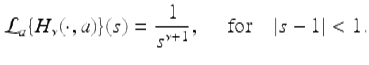
$$\displaystyle{\mathcal{L}_{a}\{H_{\nu }(\cdot,a)\}(s) = \frac{1} {s^{\nu +1}},\quad \mbox{ for}\quad \vert s - 1\vert < 1.}$$

Proof.

Consider for | s − 1 |  < 1,  | s |  p  > 1

$$\displaystyle\begin{array}{rcl} & & \mathcal{L}_{a}\{H_{\nu }(\cdot,a)\}(s) =\sum _{ k=1}^{\infty }(1 - s)^{k-1}H_{\nu }(a + k,a) =\sum _{ k=1}^{\infty }(1 - s)^{k-1} \frac{k^{\overline{\nu }}} {\Gamma (\nu +1)} {}\\ & & \quad \quad =\sum _{ k=1}^{\infty }(1 - s)^{k-1} \frac{\Gamma (k+\nu )} {\Gamma (k)\Gamma (\nu +1)} =\sum _{ k=0}^{\infty }(1 - s)^{k} \frac{\Gamma (k + 1+\nu )} {\Gamma (k + 1)\Gamma (\nu +1)} {}\\ & & \quad \quad =\sum _{ k=0}^{\infty }(1 - s)^{k} \frac{(1+\nu )^{\overline{k}}} {\Gamma (k + 1)} {}\\ & & \quad \quad =\sum _{ k=0}^{\infty }(-1)^{k}(1 - s)^{k} \frac{\Gamma (-\nu )} {\Gamma (k + 1)\Gamma (-\nu - k)}\quad \quad \quad \text{(by Lemma <InternalRef RefID="FPar73">3.73</InternalRef>)} {}\\ & & \quad \quad =\sum _{ k=0}^{\infty }(-1)^{k}(1 - s)^{k}\frac{[-(\nu +1)]^{\underline{k}}} {\Gamma (k + 1)} {}\\ & & \quad \quad =\sum _{ k=0}^{\infty }(-1)^{k}{-(\nu +1)\choose k}(1 - s)^{k} {}\\ & & \quad \quad = \left [1 - (1 - s)\right ]^{-(\nu +1)}\quad \quad \text{(by the Generalized Binomial Theorem)} {}\\ & & \quad \quad = \frac{1} {s^{\nu +1}}. {}\\ \end{array}$$

This completes the proof. □ 

Combining Theorems 3.67 and 3.74, we get the following corollary:

Corollary 3.75.

For $$\nu \in \mathbb{C}\setminus \{- 1,-2,-3,\ldots \}$$ , we have that

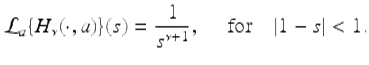
$$\displaystyle{\mathcal{L}_{a}\{H_{\nu }(\cdot,a)\}(s) = \frac{1} {s^{\nu +1}},\quad \mbox{ for}\quad \vert 1 - s\vert < 1.}$$

Theorem 3.76.

The following hold:

(i)

$$\mathcal{L}_{a}\{E_{p}(\cdot,a)\}(s) = \frac{1} {s-p},\quad p\neq 1;$$

(ii)

$$\mathcal{L}_{a}\{\mbox{ Cosh}_{p}(\cdot,a)\}(s) = \frac{s} {s^{2}-p^{2}},\quad p\neq \pm 1;$$

(iii)

$$\mathcal{L}_{a}\{\mbox{ Sinh}_{p}(\cdot,a)\}(s) = \frac{p} {s^{2}-p^{2}},\quad p\neq \pm 1;$$

(iv)

$$\mathcal{L}_{a}\{\mbox{ Cos}_{p}(\cdot,a)\}(s) = \frac{s} {s^{2}+p^{2}},\quad p\neq \pm i;$$

(v)

$$\mathcal{L}_{a}\{\mbox{ Sin}_{p}(\cdot,a)\}(s) = \frac{p} {s^{2}+p^{2}},\quad p\neq \pm i;$$

where (i) holds for $$\vert s - 1\vert < \vert 1 - p\vert $$ , (ii) and (iii) hold for $$\vert s - 1\vert < \mbox{ min}\{\vert 1 - p\vert,\vert 1 + p\vert \},$$ and (iv) and (v) hold for $$\vert s - 1\vert < \mbox{ min}\{\vert 1 - ip\vert,\vert 1 + ip\vert \}$$ .

Proof.

To see that (i) holds, note that

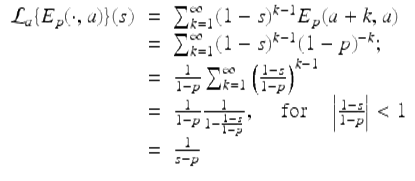
$$\displaystyle\begin{array}{rcl} \mathcal{L}_{a}\{E_{p}(\cdot,a)\}(s)& =& \sum _{k=1}^{\infty }(1 - s)^{k-1}E_{ p}(a + k,a) {}\\ & =& \sum _{k=1}^{\infty }(1 - s)^{k-1}(1 - p)^{-k}; {}\\ & =& \frac{1} {1 - p}\sum _{k=1}^{\infty }\left (\frac{1 - s} {1 - p}\right )^{k-1} {}\\ & =& \frac{1} {1 - p} \frac{1} {1 -\frac{1-s} {1-p}},\quad \mbox{ for}\quad \left \vert \frac{1 - s} {1 - p}\right \vert < 1 {}\\ & =& \frac{1} {s - p} {}\\ \end{array}$$

for $$\vert s - 1\vert < \vert 1 - p\vert $$ . To see that (ii) holds, note that for $$\vert s - 1\vert <\min \{ \vert 1 - p\vert,\vert 1 + p\vert \}$$

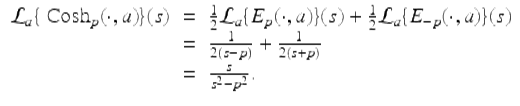
$$\displaystyle\begin{array}{rcl} \mathcal{L}_{a}\{\mbox{ Cosh}_{p}(\cdot,a)\}(s)& =& \frac{1} {2}\mathcal{L}_{a}\{E_{p}(\cdot,a)\}(s) + \frac{1} {2}\mathcal{L}_{a}\{E_{-p}(\cdot,a)\}(s) {}\\ & =& \frac{1} {2(s - p)} + \frac{1} {2(s + p)} {}\\ & =& \frac{s} {s^{2} - p^{2}}. {}\\ \end{array}$$

To see that (iv) holds, note that

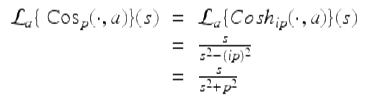
$$\displaystyle\begin{array}{rcl} \mathcal{L}_{a}\{\mbox{ Cos}_{p}(\cdot,a)\}(s)& =& \mathcal{L}_{a}\{Cosh_{ip}(\cdot,a)\}(s) {}\\ & =& \frac{s} {s^{2} - (ip)^{2}} {}\\ & =& \frac{s} {s^{2} + p^{2}} {}\\ \end{array}$$

for $$\vert s - 1\vert <\min \{ \vert 1 - ip\vert,\vert 1 + ip\vert \}$$ . The proofs of parts (iii) and (v) are left as an exercise (Exercise 3.31). □