Delta Trigonometric Functions - Basic Difference Calculus

Discrete Fractional Calculus (2015)

1. Basic Difference Calculus

1.3. Delta Trigonometric Functions

In this section we introduce the delta hyperbolic sine and cosine functions, the delta sine and delta cosine functions and give some of their properties. First, we define the delta hyperbolic sine and cosine functions.

Definition 1.24.

Assume $\pm p \in \mathcal{R}$ . Then the delta hyperbolic sine and the delta hyperbolic cosine functions are defined as follows:

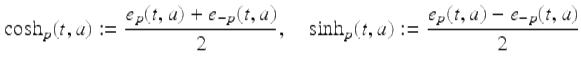
$\displaystyle{\cosh _{p}(t,a):= \frac{e_{p}(t,a) + e_{-p}(t,a)} {2},\quad \sinh _{p}(t,a):= \frac{e_{p}(t,a) - e_{-p}(t,a)} {2} }$

for $t \in \mathbb{N}_{a}.$

The following theorem gives various properties of the delta hyperbolic sine and cosine functions.

Theorem 1.25.

Assume $\pm p \in \mathcal{R}$ . Then

(i)

$\cosh _{p}(a,a) = 1,\quad \sinh _{p}(a,a) = 0;$

(ii)

$\cosh _{p}^{2}(t,a) -\sinh _{p}^{2}(t,a) = e_{-p^{2}}(t,a),\quad t \in \mathbb{N}_{a};$

(iii)

$\Delta \cosh _{p}(t,a) = p(t)\;\sinh _{p}(t,a),\quad t \in \mathbb{N}_{a};$

(iv)

$\Delta \sinh _{p}(t,a) = p(t)\;\cosh _{p}(t,a),\quad t \in \mathbb{N}_{a};$

(v)

$\cosh _{-p}(t,a) =\cosh _{p}(t,a),\quad t \in \mathbb{N}_{a};$

(vi)

$\sinh _{-p}(t,a) = -\sinh _{p}(t,a),\quad t \in \mathbb{N}_{a};$

(vii)

$e_{p}(t,a) =\cosh _{p}(t,a) +\sinh _{p}(t,a),\quad t \in \mathbb{N}_{a}.$

Proof.

Clearly (i) holds. To see that (ii) holds note that

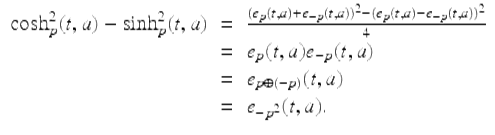
$\displaystyle\begin{array}{rcl} \cosh _{p}^{2}(t,a) -\sinh _{ p}^{2}(t,a)& =& \frac{(e_{p}(t,a) + e_{-p}(t,a))^{2} - (e_{ p}(t,a) - e_{-p}(t,a))^{2}} {4} {}\\ & =& e_{p}(t,a)e_{-p}(t,a) {}\\ & =& e_{p\oplus (-p)}(t,a) {}\\ & =& e_{-p^{2}}(t,a). {}\\ \end{array}$

To see that (iii) holds, consider

$\displaystyle\begin{array}{rcl} \Delta \cosh _{p}(t,a)& =& \frac{1} {2}\Delta e_{p}(t,a) + \frac{1} {2}\Delta e_{-p}(t,a) {}\\ & =& \frac{1} {2}[p(t)e_{p}(t,a) - p(t)e_{-p}(t,a)] {}\\ & =& p(t)\;\sinh _{p}(t,a). {}\\ \end{array}$

The proof of (iv) is similar. The proofs of (v) and (vi) are trivial. The formula in part (vii) we call the (delta) hyperbolic Euler’s formula and its proof follows from the definitions of the hyperbolic sine and hyperbolic cosine functions. □

We next define the delta sine and cosine functions.

Definition 1.26.

For $\pm ip \in \mathcal{R}$ , we define the delta sine function and delta cosine function as follows:

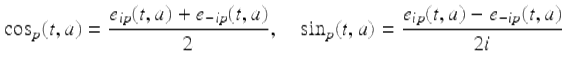
$\displaystyle{\cos _{p}(t,a) = \frac{e_{ip}(t,a) + e_{-ip}(t,a)} {2},\quad \sin _{p}(t,a) = \frac{e_{ip}(t,a) - e_{-ip}(t,a)} {2i} }$

for $t \in \mathbb{N}_{a}.$

The following theorem gives some relationships between the delta trigonometric functions and the delta hyperbolic trigonometric functions.

Theorem 1.27.

Assume $\pm p \in \mathcal{R}$ . Then

(i)

$\sin _{ip}(t,a) = i\sinh _{p}(t,a);$

(ii)

$\cos _{ip}(t,a) =\cosh _{p}(t,a);$

(iii)

$\sinh _{ip}(t,a) = i\sin _{p}(t,a);$

(iv)

$\cosh _{ip}(t,a) =\cos _{p}(t,a),$

for $t \in \mathbb{N}_{a}.$

Proof.

To see that (i) holds note that

$\displaystyle\begin{array}{rcl} \sin _{ip}(t,a)& =& \frac{1} {2i}[e_{i^{2}p}(t,a) - e_{-i^{2}p}(t,a)] {}\\ & =& i\frac{e_{p}(t,a) - e_{-p}(t,a)} {2} {}\\ & =& i\sinh _{p}(t,a). {}\\ \end{array}$