High School Geometry Unlocked (2016)

Lesson 3.2. Triangle Similarity

As we learned in Chapter 2, triangles have a certain amount of predictability, which allows us to make some conclusions from limited information. In this lesson, we’ll introduce three postulates that you can use to prove triangle similarity. Note that these postulates do not work to establish congruence, only similarity.

SSS (SIDE-SIDE-SIDE) SIMILARITY POSTULATE

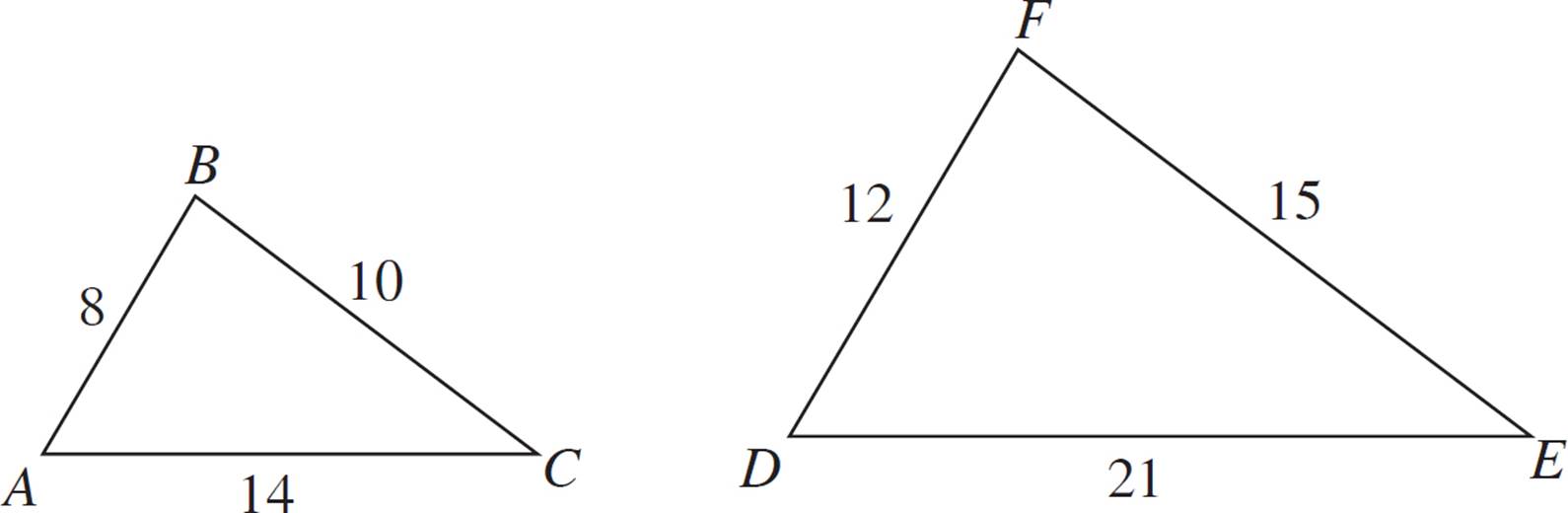
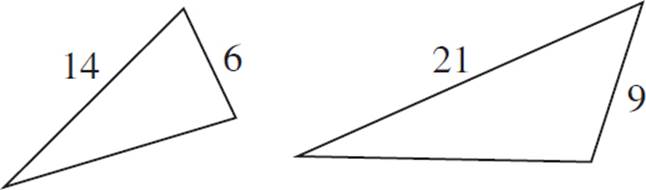
Are triangles ABC and DEF similar?

In order to prove that these triangles are similar, we can try to prove that there is a constant ratio between the corresponding sides.

Sides AB and DF correspond, since each is the smallest side of its respective triangle. The ratio of AB to DF is 8 to 12, or . This reduces to .

The next largest pair of corresponding sides is BC and FE. The ratio of BC to FE is 10 to 15, or . This reduces to .

The last pair of corresponding sides is AC and DE. The ratio of AC to DE is 14 to 21, or . This reduces to .

All three pairs of corresponding sides are proportional, with a constant ratio of . Therefore, using the definition of similarity, we know that triangles ABC and DEF are similar.

SSS (Side-Side-Side) Similarity Postulate

Two triangles are similar if all three pairs of corresponding sides are proportional.

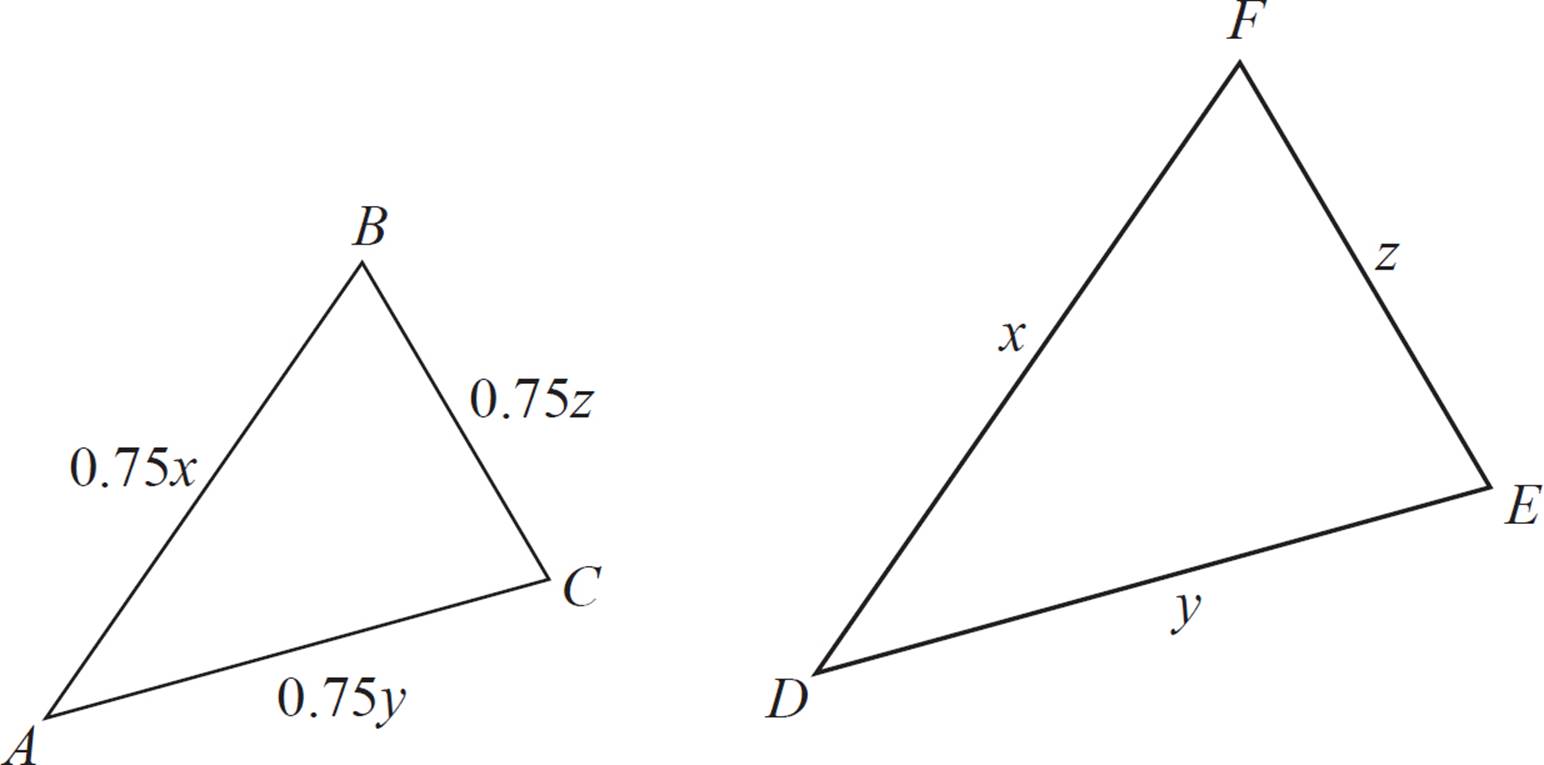
Are triangles ABC and DEF similar?

This example has just about the same idea as the previous example, but with algebraic expressions instead of numerical values. Here, each pair of corresponding sides shares a variable in common (x, y, or z). You just need to compare the ratios of the corresponding sides. You can easily see that each pair has the same ratio.

Sides AB and DF correspond, with a ratio of 0.75x to 1x. This simplifies to 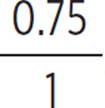, or .

Sides BC and FE correspond, with a ratio of 0.75y to 1y. This simplifies to 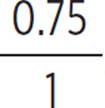, or .

Sides AC and DE correspond, with a ratio of 0.75z to 1z. This simplifies to 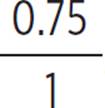, or .

All three pairs of corresponding sides are proportional, with a constant ratio of . Therefore, using the definition of similarity, we know that triangles ABC and DEF are similar.

SSS Similarity Postulate Exercise

For each of the pairs of triangles below, write “yes” if the triangles can be proved to be similar to the information provided; otherwise, write “no.”

Complete the exercise on your own. Answers can be found at the end of the chapter.

AAA (ANGLE-ANGLE-ANGLE) SIMILARITY POSTULATE

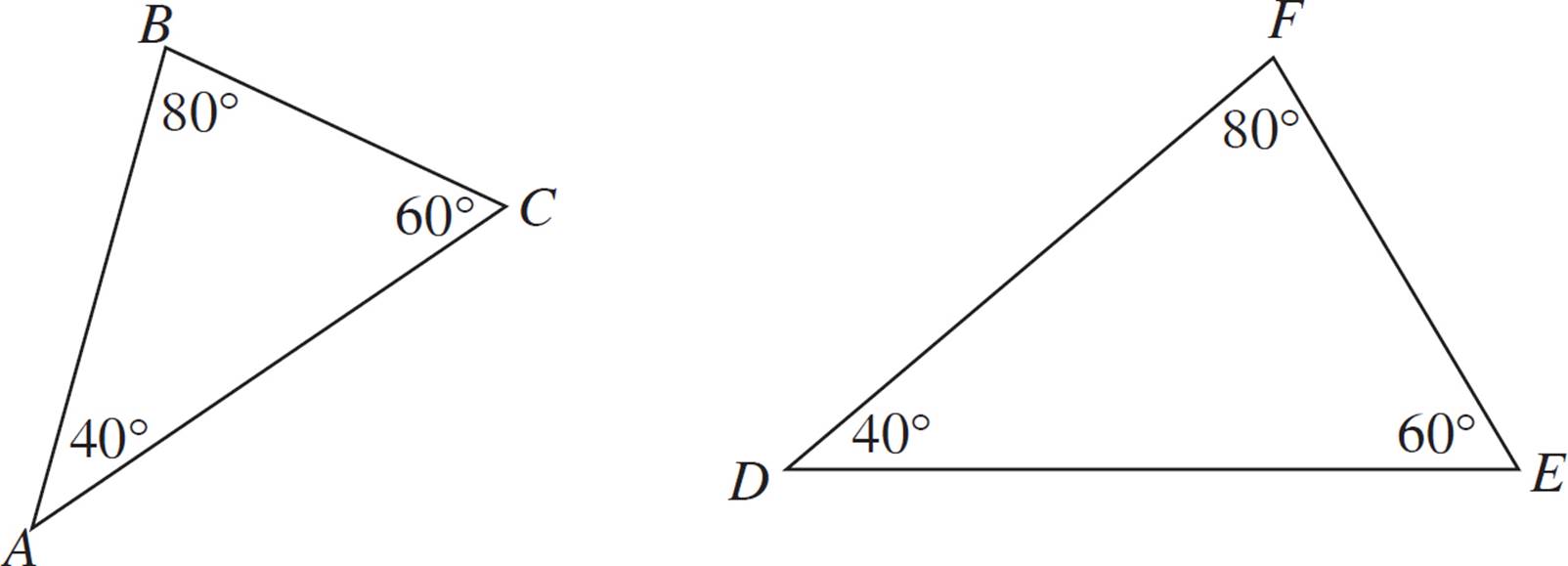
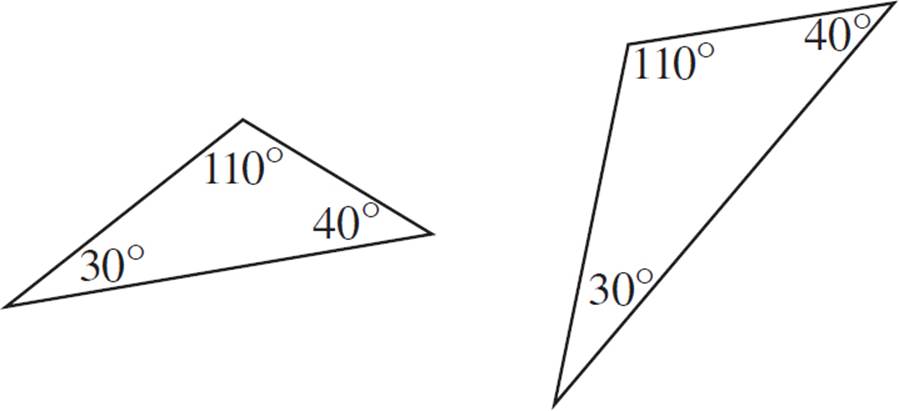
Are triangles ABC and DEF similar?

One way to show how this postulate works is to make the triangles overlap. Let’s place triangle ABC within triangle DEF so that they share a common angle.

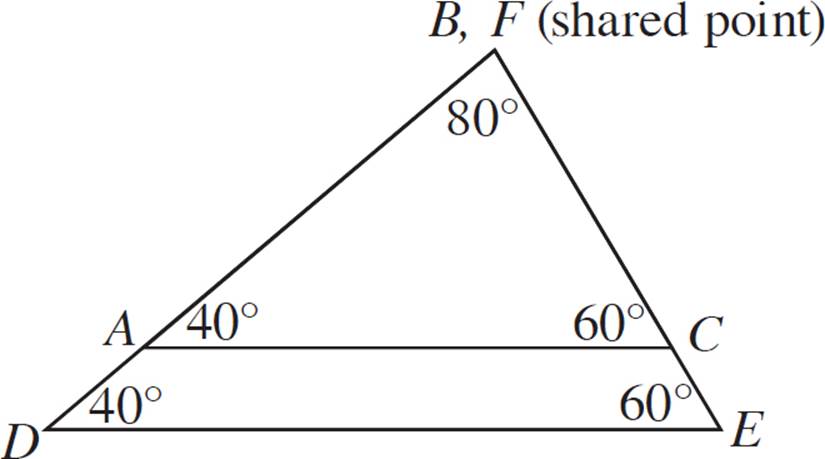
Here, we can prove that segment AC is parallel to segment DE. That’s because the corresponding angles are congruent. (Angle BAC corresponds with angle FDE, and angle BCA corresponds with angle FED). Additionally, segments AB and DF overlap each other (they lie on the same line), as do segments BC and FE. The triangles are the exact same shape, but they are different sizes. Therefore, they are similar.

AAA (Angle-Angle-Angle) Similarity Postulate

Two triangles are similar if all three pairs of corresponding angles are congruent.

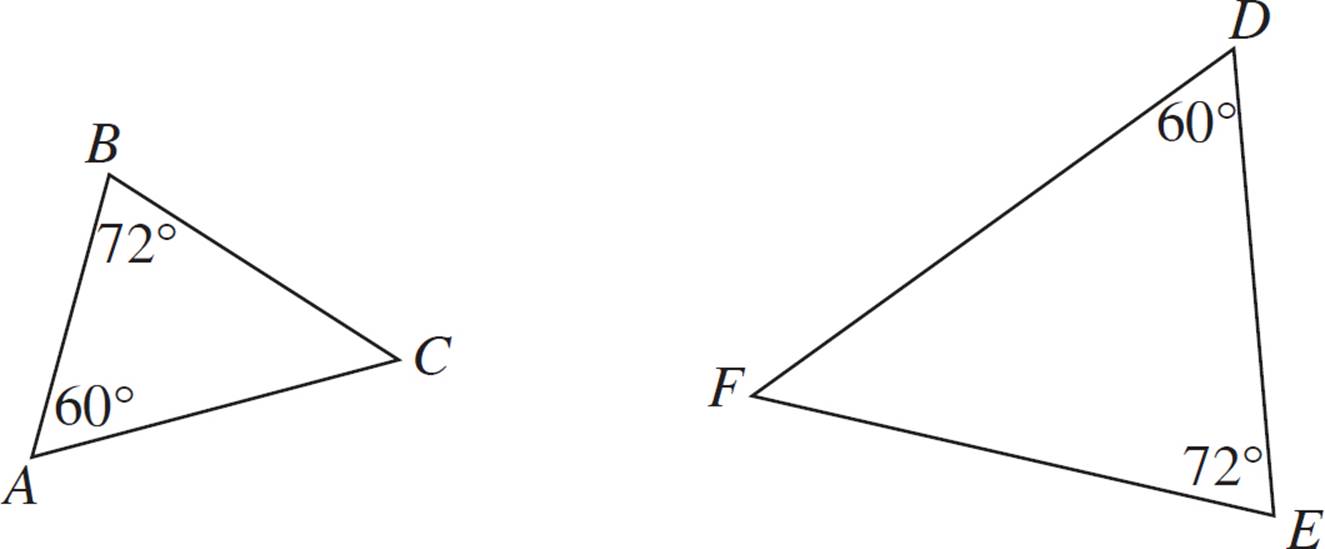
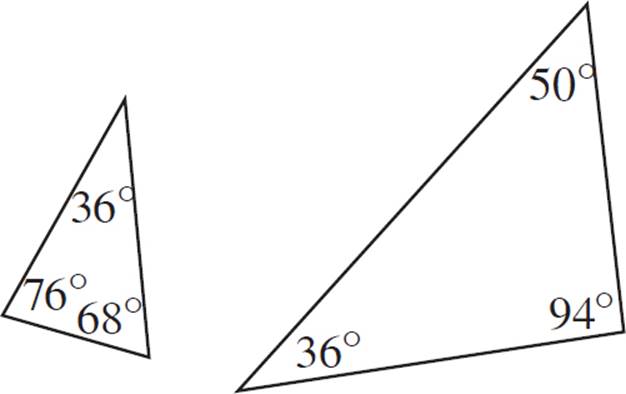
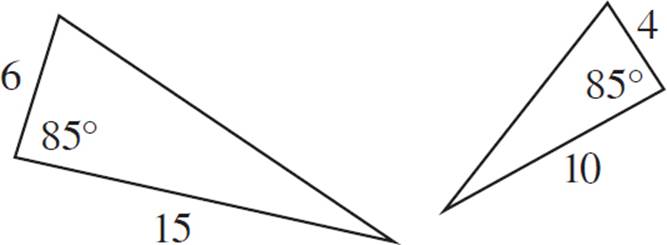
Are triangles ABC and DEF similar?

In this example, only two pairs of angles are shown. Are the triangles still similar? Consider what you know about this figure. The sum of angles in any triangle must be 180°. Therefore, you can solve for the missing angle in both triangles.

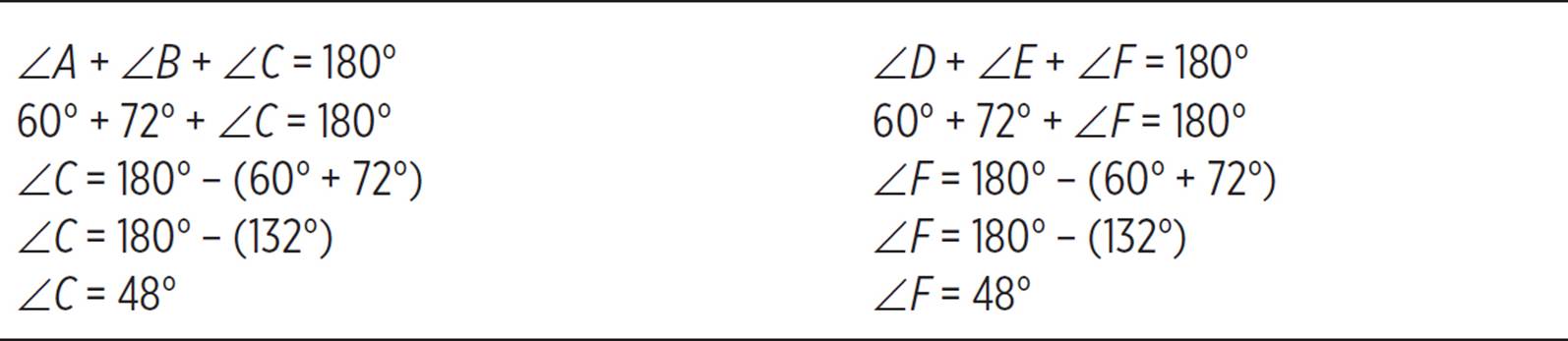
Therefore, all of the angles are known, not just two.

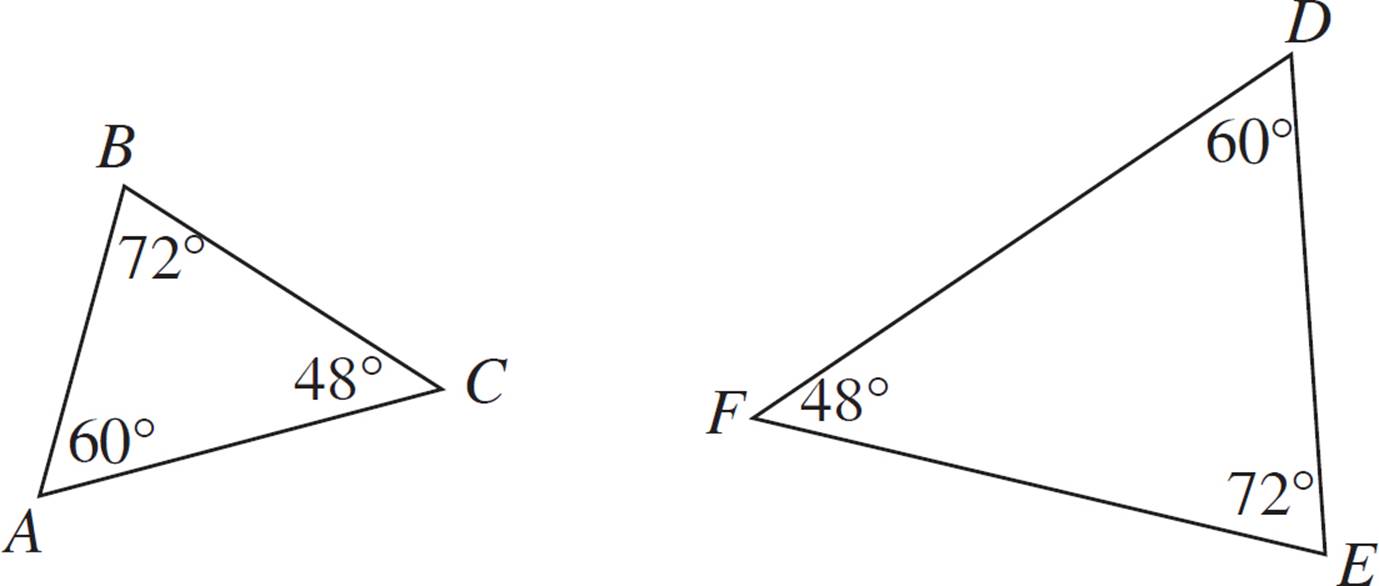
We can apply the AAA Similarity Postulate if we know that we have two pairs of corresponding angles that are congruent.

Here is how you may see the triangle similarity on the ACT.

Two similar triangles have perimeters in the ratio 5:6. The sides of the larger triangle measure 12 in, 7 in, and 5 in. What is the perimeter, in inches, of the smaller triangle?

F.18

G.20

H.22

J.24

K.32

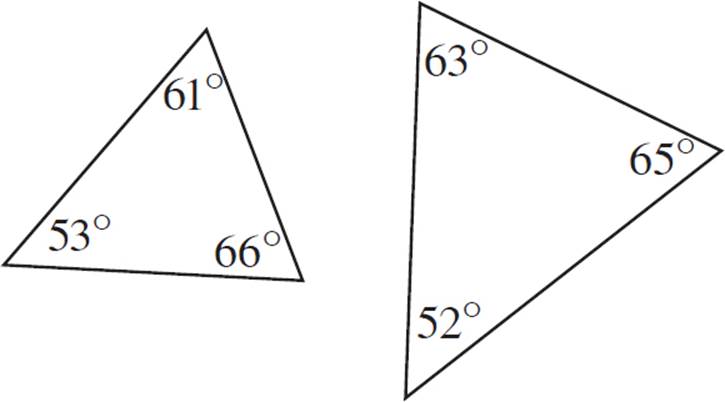
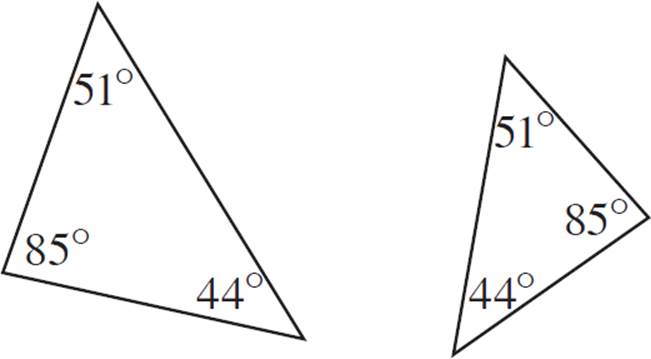
AAA Similarity Postulate Exercise

For each of the pairs of triangles below, write “yes” if the triangles can be proved to be similar to the information provided; otherwise, write “no.”

Complete the exercise on your own. Answers can be found at the end of the chapter.

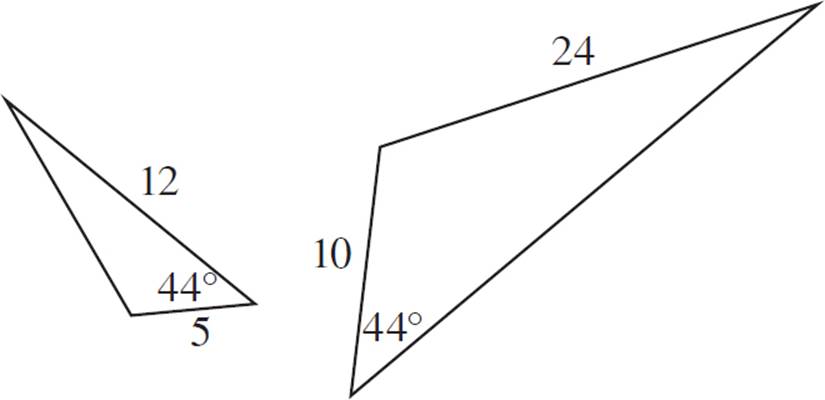
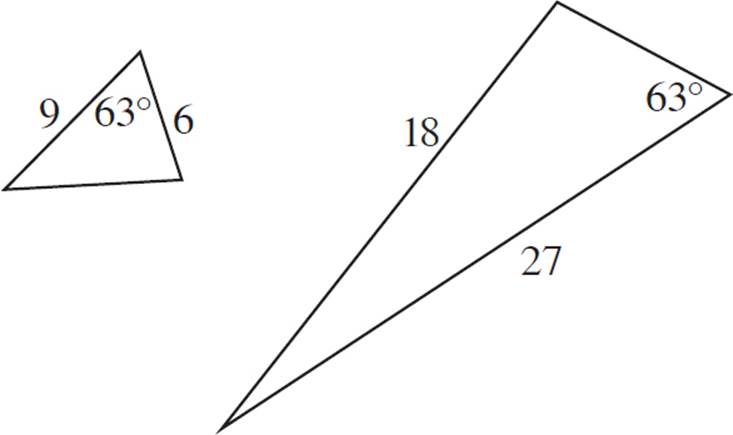
SAS (SIDE-ANGLE-SIDE) SIMILARITY POSTULATE

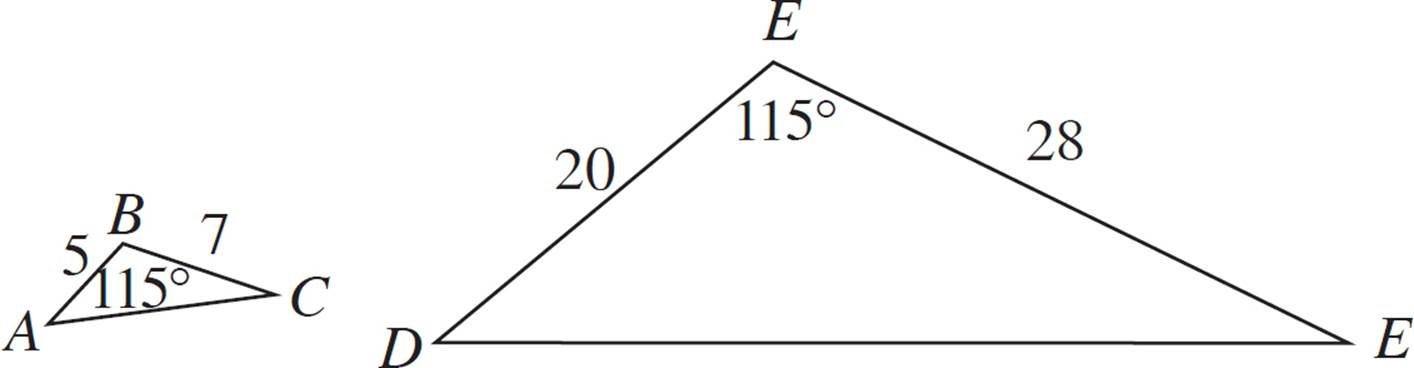
Are triangles ABC and DEF similar?

In this example, we have two sides given for each triangle, as well as the included angle of each pair. We also know that the two angles are congruent. Next, compare the corresponding sides to see if there is a constant ratio among them.

Sides AB and DE correspond, since they are each the smallest side of their respective triangles. The ratio of AB to DE is 5 to 20, or . This reduces to .

The next largest pair of corresponding sides is BC and EF. The ratio of BC to EF is 7 to 28, or 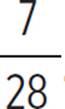. This reduces to .

The two pairs of corresponding given sides are proportional, with a constant ratio of .

The perimeter of the larger triangle is 12 in. + 7 in. + 5 in. = 24 in. Since you know the ratio of the perimeters, you do not have to find each side of the smaller triangle; you can set up the following ratio:

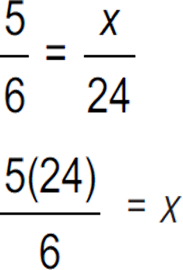
x = 20 in

Therefore, the answer is (G).

How do we know if the third sides are proportional as well?

Let’s overlap these triangles, with the common angle as a shared point.

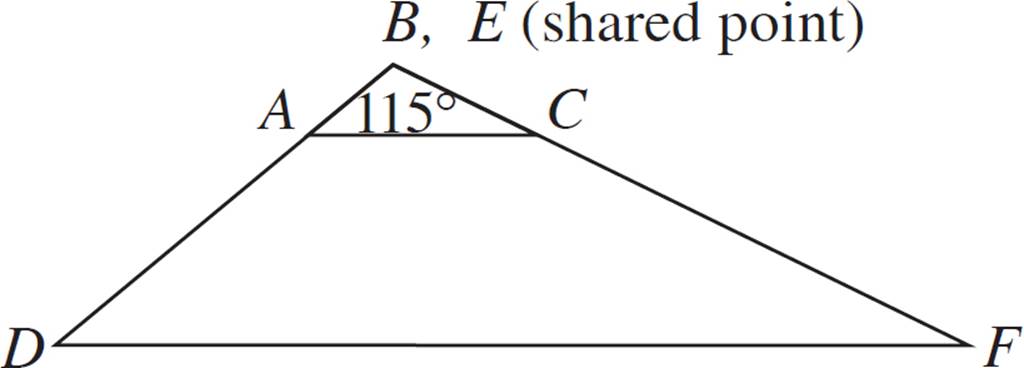
With the figures overlapping, it’s easy to see that sides AC and DF appear to be parallel. In fact, we can prove that they are parallel because the given pairs of corresponding sides have a common ratio of . That is, points A and C are both of the distance away from the shared vertex, and that means that the slope of AC is the same as that of DF.

Since AC and DF are parallel, we know that the corresponding angles BAC and EDF are congruent, as well as the corresponding angles ACB and DFE. Therefore, all three pairs of corresponding angles are congruent, and using the definition of similarity, we know that triangles ABC and DEF are similar.

SAS (Side-Angle-Side) Similarity Postulate

Two triangles are similar if two pairs of corresponding sides are proportional and the included angles are congruent.

SAS Similarity Postulate Exercise

For each of the pairs of triangles below, write “yes” if the triangles can be proved to be similar with the information provided; otherwise, write “no.”

Complete the exercise on your own. Answers can be found at the end of the chapter.

ANSWERS TO CHAPTER 3 EXERCISES

SSS Similarity Postulate Exercise

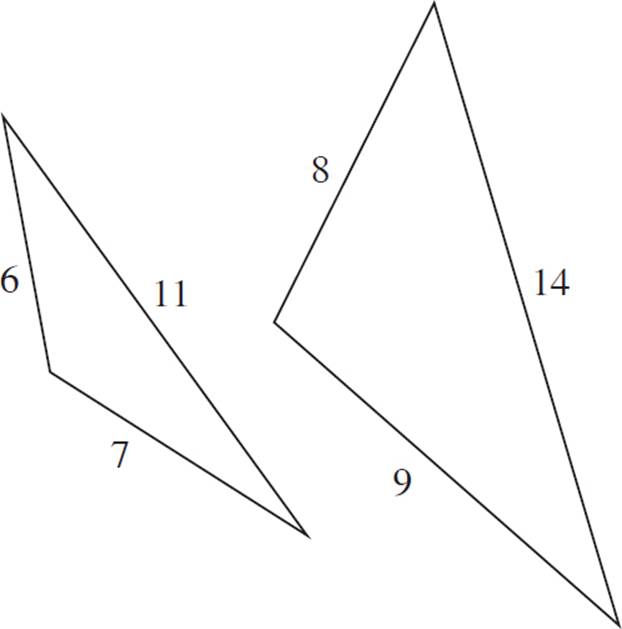
1.No.

These triangles do not have proportional sides; the ratios of corresponding sides are 6:8 (or 3:4), 7:9, and 11:14, respectively. Therefore, they are not similar.

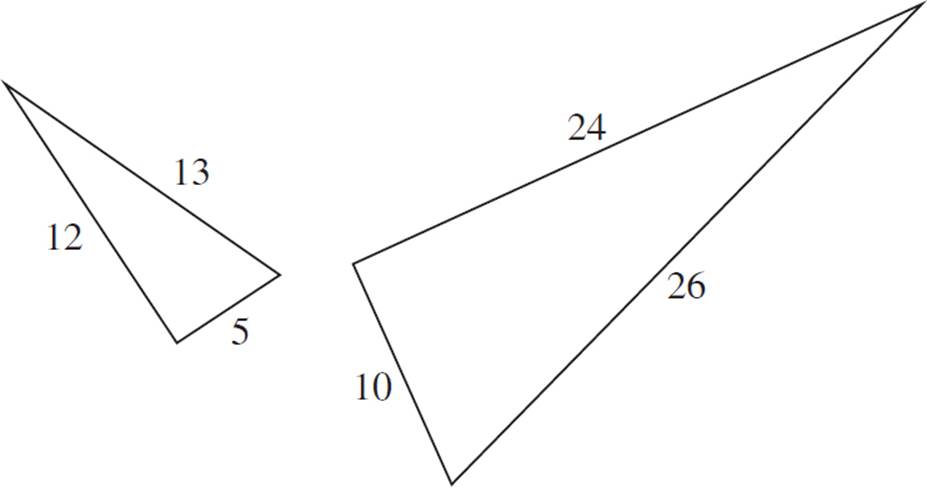
2.Yes.

These triangles have the same proportions for all three pairs of corresponding sides; therefore, they are similar.

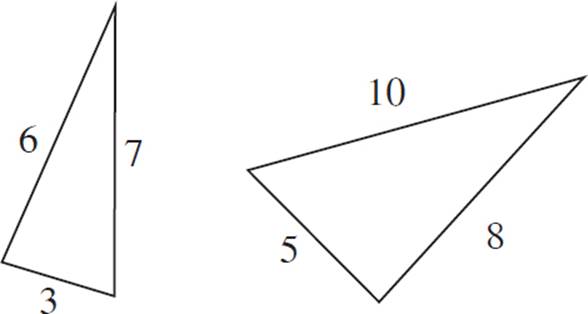
3.No.

These triangles have two pairs of proportional sides (both 3:5 and 6:10 reduce to 3:5). However, the third pair of corresponding sides is not in the same proportion (7:8). Therefore, they are not similar.

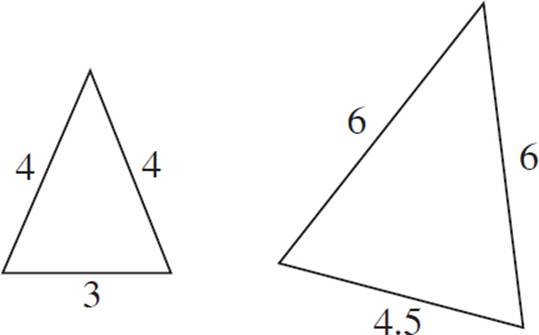
4.Yes.

These triangles have the same proportions for all three pairs of corresponding sides; therefore, they are similar.

5.No.

These triangles have two pairs of proportional sides (both 6:14 and 9:21 reduce to 3:7). However, one side length is unknown; therefore, they are not necessarily similar.

6.Yes.

These triangles have the same proportions for all three pairs of corresponding sides; therefore, they are similar.

AAA Similarity Postulate Exercise

1.Yes.

These triangles have three pairs of congruent corresponding angles; therefore, they are similar.

2.No.

These triangles do not have congruent corresponding angles. Therefore, they are not similar.

3.No.

These triangles have only one pair of corresponding congruent angles. However, the other pairs are not congruent. Therefore, the triangles are not similar.

4.Yes.

These triangles have three pairs of congruent corresponding angles; therefore, they are similar.

5.No.

These triangles have pairs of angles that are close in measure, but the angles are not congruent. We cannot apply AAA if the angles are not exactly congruent. Therefore, these triangles are not similar.

6.Yes.

These triangles each have two known angles, which means that the third angle can be derived for each as well. These triangles have three pairs of congruent corresponding angles; therefore, they are similar.

SAS Similarity Postulate Exercise

1.Yes.

These triangles have the same proportions for both pairs of corresponding sides, and the included angles are congruent; therefore, they are similar.

2.No.

These triangles do not have proportional sides; the ratios of corresponding sides are 5:15 (or 1:3) and 6:13, respectively. Therefore, they are not similar.

3.No.

These triangles have two pairs of proportional sides (both 3:7 and 9:21 reduce to 3:7). However, the included angles are not congruent. Therefore, they are not similar.

4.Yes.

These triangles have the same proportions for both pairs of corresponding sides, and the included angles are congruent; therefore, they are similar.

5.No.

These triangles have two pairs of proportional sides (both 6:18 and 9:27 reduce to 1:3). However, the given angles do not correspond (they are in a different place in the two triangles). Therefore, the triangles are not similar.

6.Yes.

These triangles have the same proportions for both pairs of corresponding sides, and the included angles are congruent; therefore, they are similar.

DRILL

CHAPTER 3 PRACTICE QUESTIONS

Directions: Complete the following problems as specified by each question. For extra practice after answering each question, try using an alternative method to solve the problem or check your work. Larger, printable versions of images are available in your online student tools.

Click here to download a PDF of Chapter 3 Practice Questions.

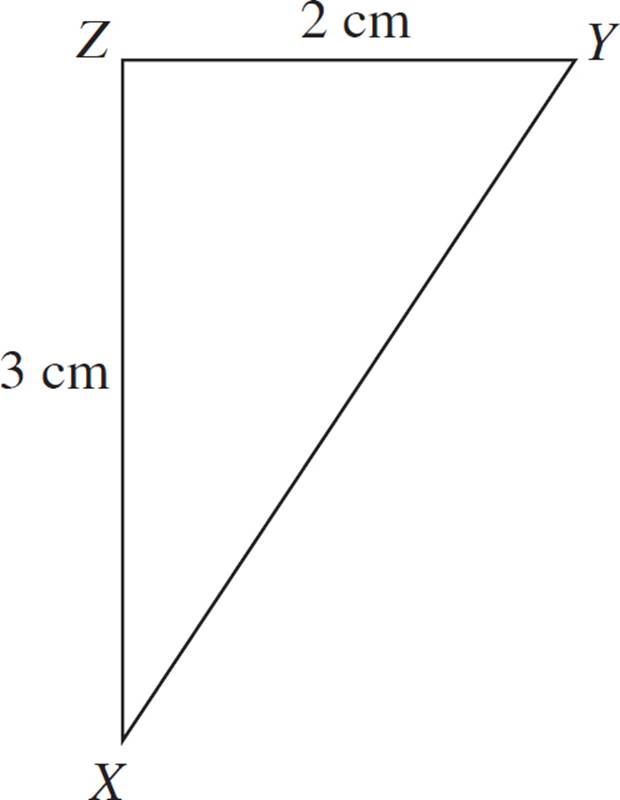
1.Construct a dilated version of triangle XYZ with a scale factor of 2.5 and the center of dilation at vertex Z.

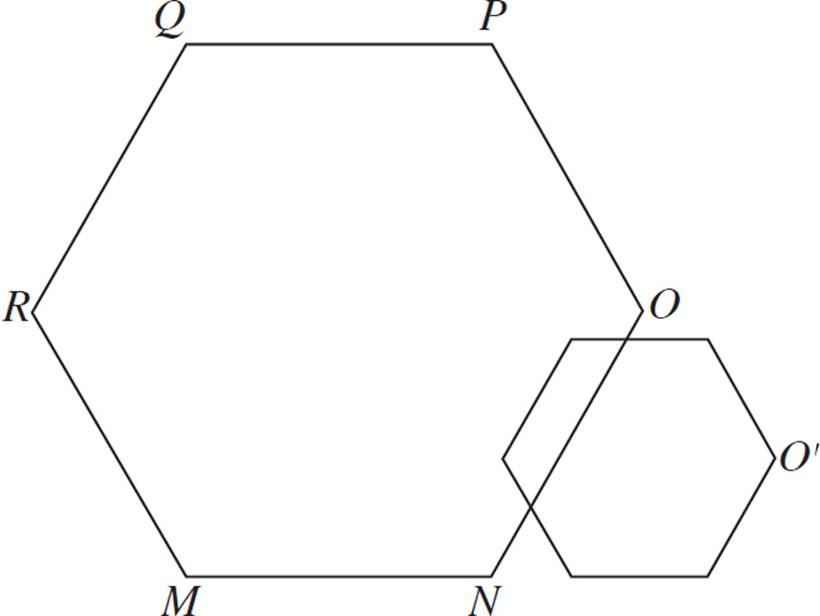
2.In the figure below, hexagon MNOPQR is dilated with a scale factor of 0.5. Find the center of dilation.

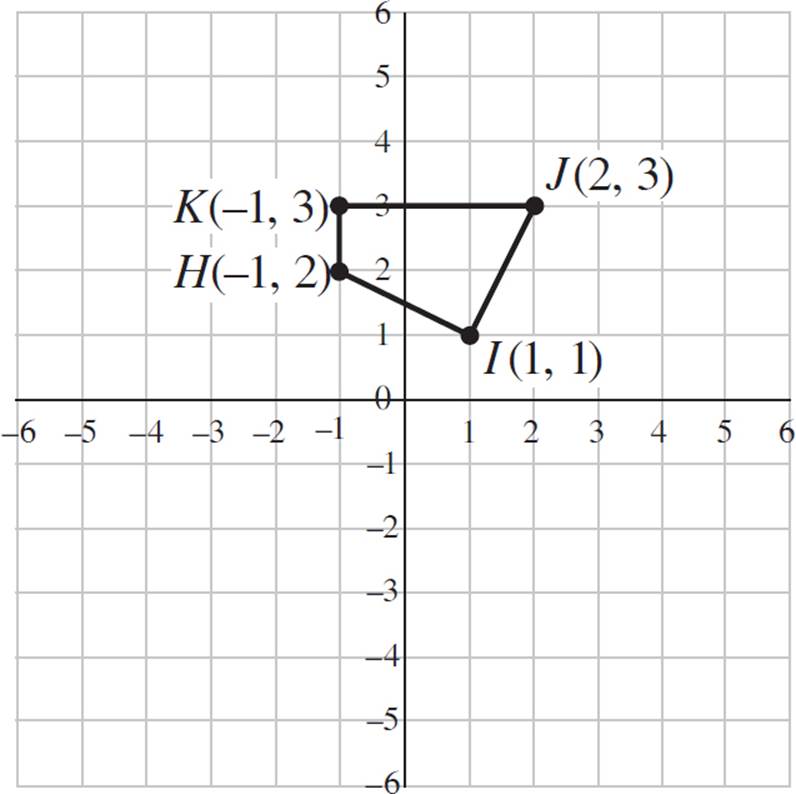
3.Construct a dilated version of quadrilateral HIJK, shown below, with a scale factor of 2 and the center of dilation at (0, 0).

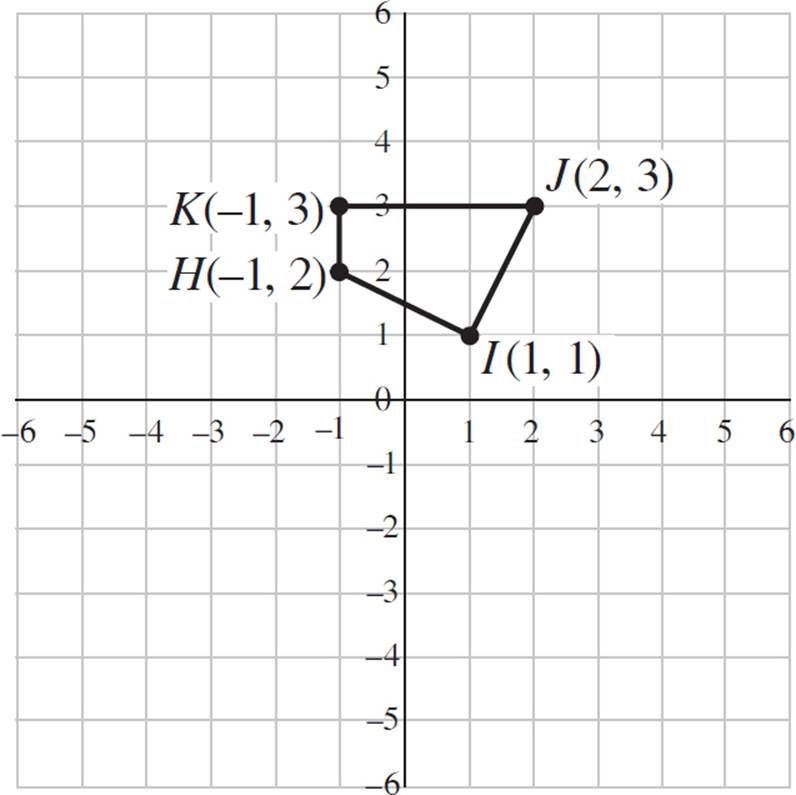
4.Construct a dilated version of quadrilateral HIJK, shown below, with a scale factor of 2 and the center of dilation at (−1, −1).

5.Construct a dilated version of the line y = 2x + 5 with a scale factor of 0.5 and a center of dilation at (0, 0). Show both the original line and the dilation on the graph. Determine the equation of the dilated line.

6.A contractor has drawn a rectangular kitchen on a coordinate grid using the points (5, 9), (5, 21), (−1, 9), and (−1, 21). The client, however, would like each dimension of the kitchen to be 1.5 times the current size. The point (−1, 9) will be kept the same. What will be the other three points?

7.A jogger travels 3 miles due west from her home to the park, 4 miles due north from the park to the lake, and 5 miles from the lake directly back home every morning. One morning she decides to extend her jog and travel one additional mile due west and one additional mile due north before jogging home. Do the two routes represent similar triangles? Explain.

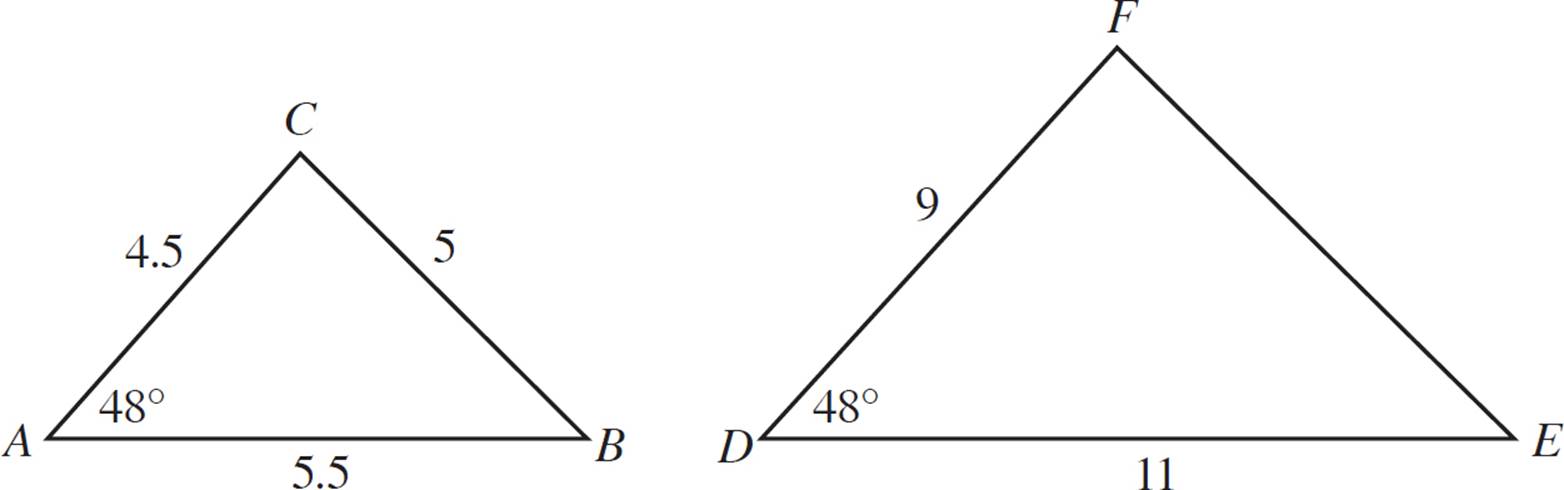
8.If possible, calculate the length of side EF without using trigonometry.

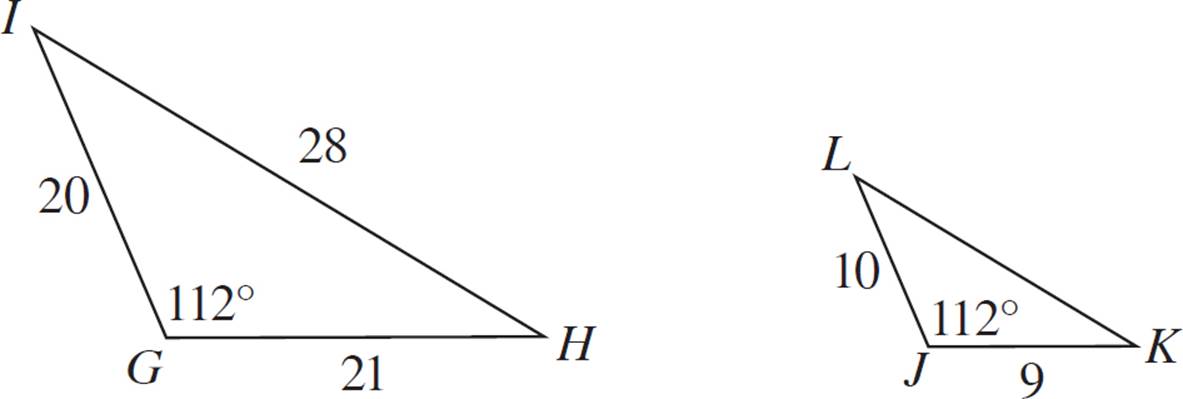
9.If possible, calculate the length of side KL without using trigonometry.

SOLUTIONS TO CHAPTER 3 PRACTICE QUESTIONS

1.

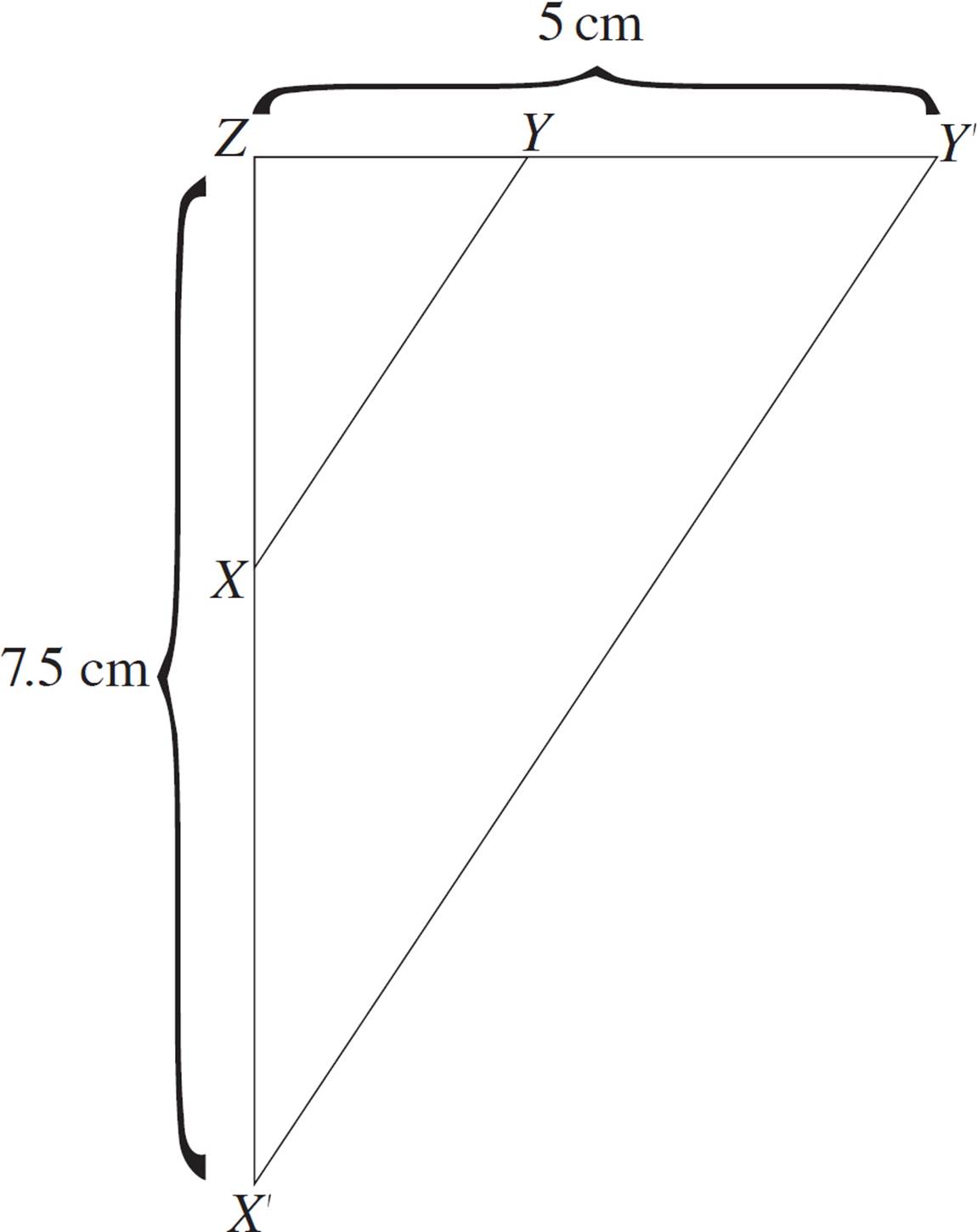
The scale factor is 2.5. Multiply the length of each segment by 2.5 to determine the lengths for the dilated triangle. Segment ZX′ will be 7.5 cm (3 ✕ 2.5), and segment ZY′ will be 5 cm (2 ✕ 2.5). Next, draw these new segments: extend segment ZX to a length of 7.5 cm and segment ZY to a length of 5 cm. Since Z is the center of dilation, this is the originating point for your measurements. Finally, connect segment X′Y′ to have the full dilated triangle. You can also verify that segment X′Y′ is 2.5 times the length of segment XY (this is optional).

2.

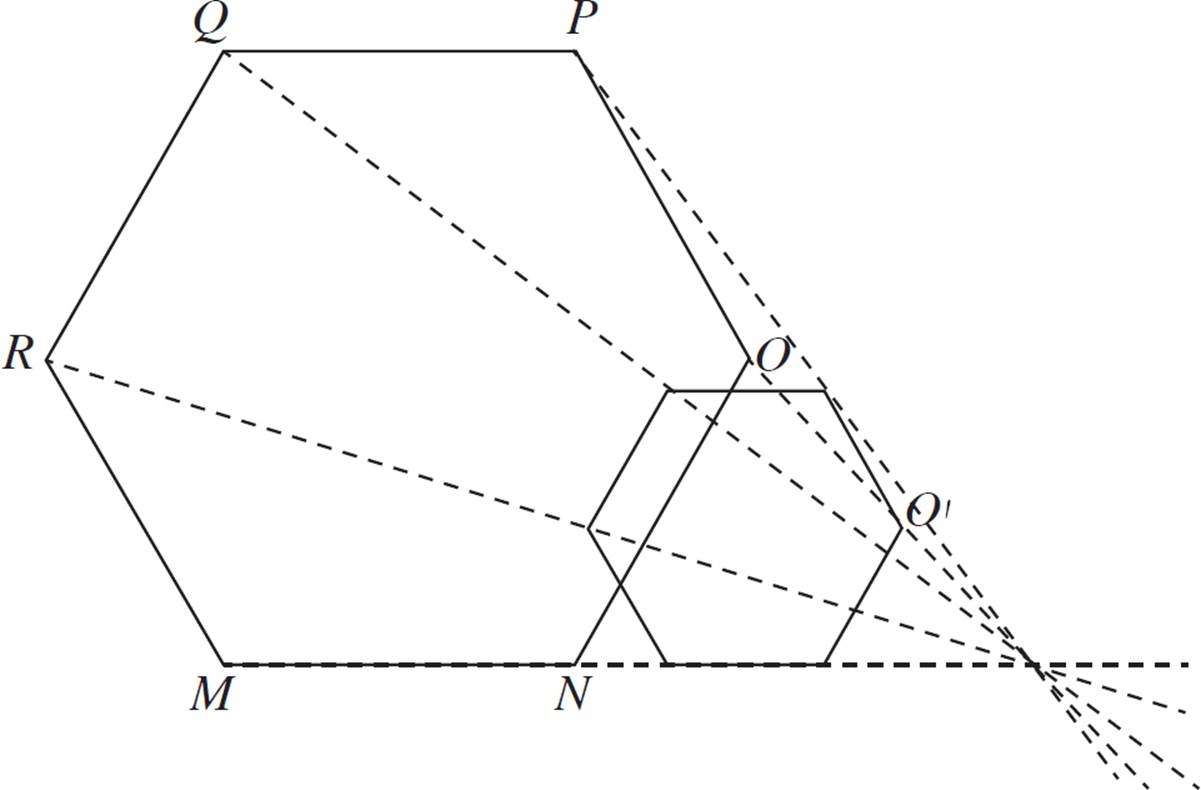
For each point on MNOPQR, draw a line through that point and its corresponding point on the dilation. These lines should all intersect at a single point, which is the center of dilation. Note: You can find the intersection point with just two of these lines! But the more lines you draw, the more likely that you can avoid mistakes and be more confident in your answer.

Note: If you do draw all of these lines, it can be a bit difficult to get the intersection point to be 100% precise. This is most likely due to understandable human error with your pencil and ruler. However, you should keep practicing dilations to get them as precise as possible!

3.

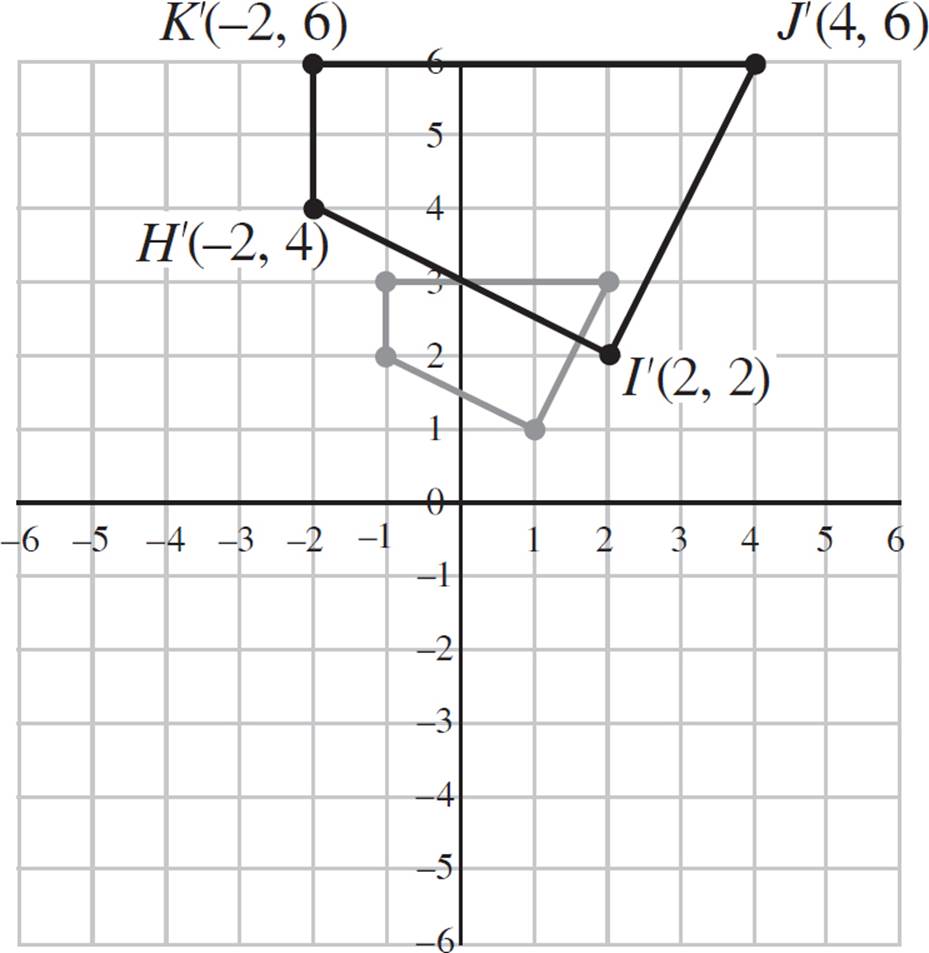
Since the center of dilation is at the origin, multiply each coordinate by the scale factor of 2. The new vertices are (−2, 4), (2, 2), (4, 6), and (−2, 6).

4.

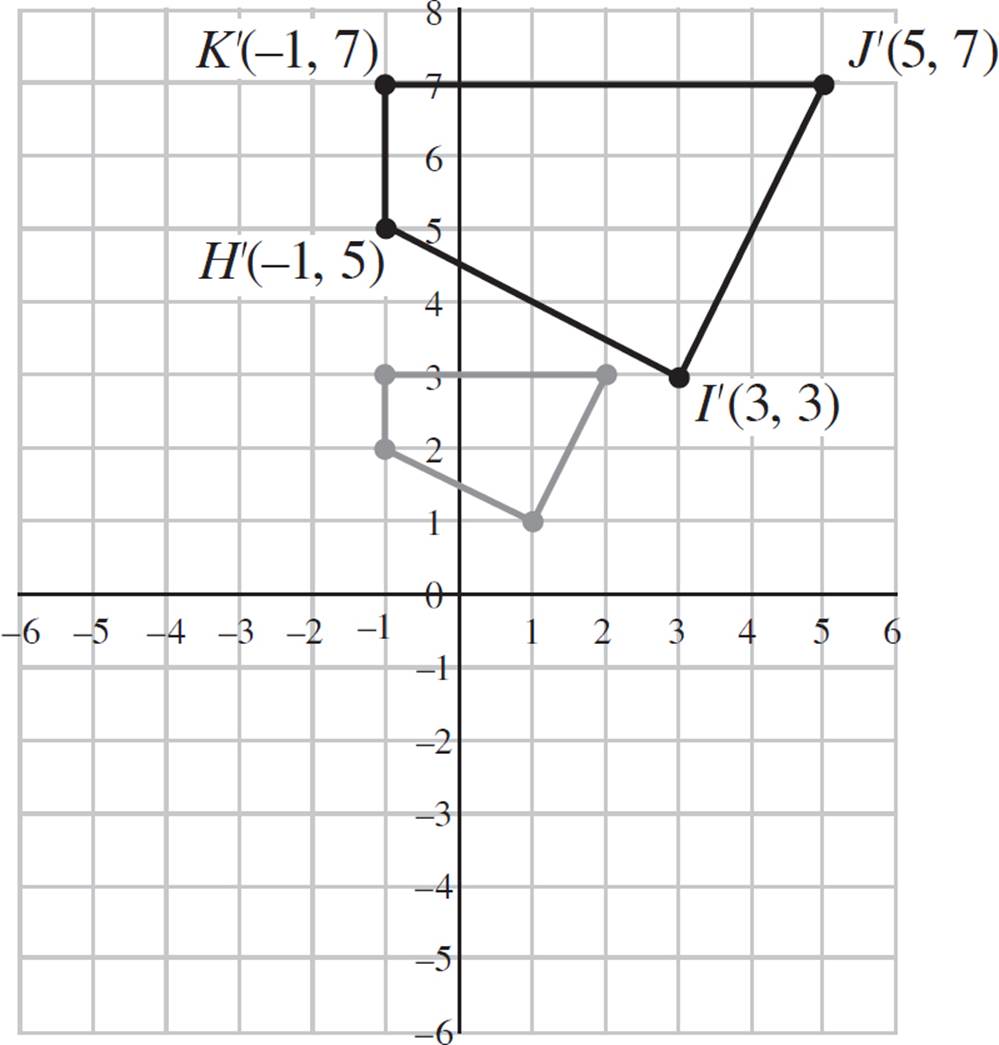
Follow the steps discussed in the lesson:

5.

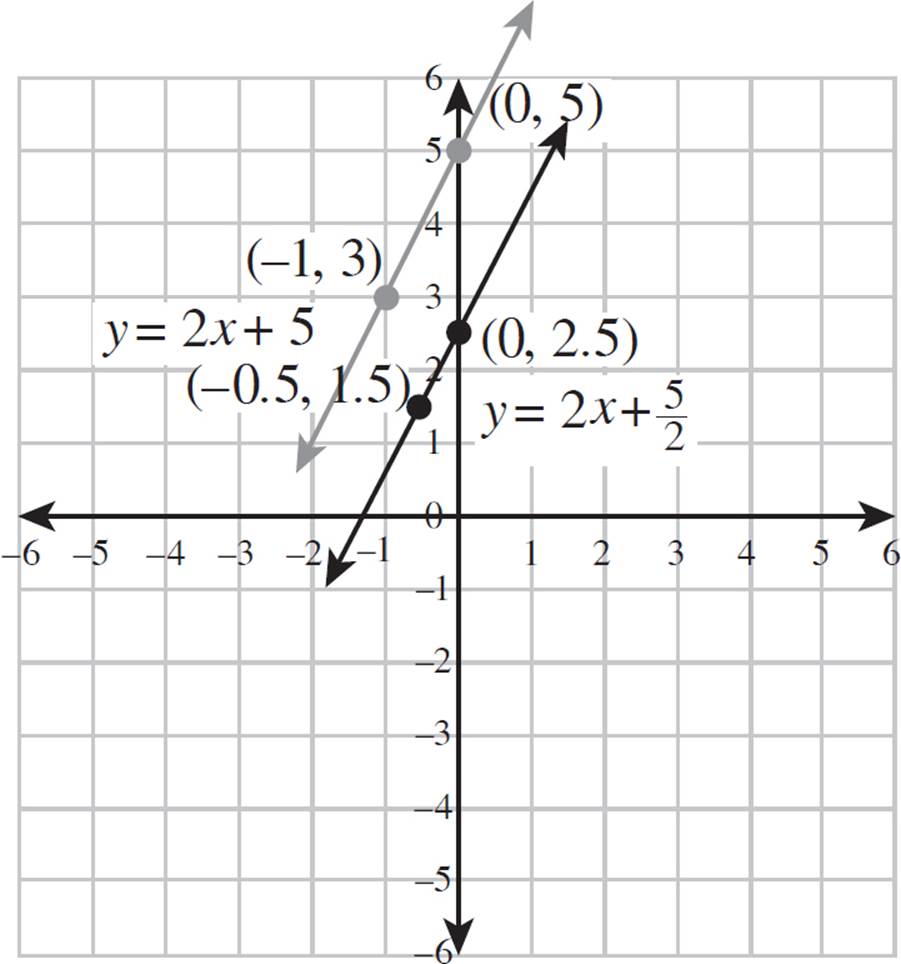
Start by finding two points on the line y = 2x + 5. One easy point is the y-intercept, where x = 0. When x = 0, y = 5. One point is (0, 5). Now find another point. Try putting in −1 for x. In that case, y = 3. A second point is (−1, 3). Now draw both points on the graph and connect them to draw the complete line. Since the center of dilation is at the origin, each point just needs to be multiplied by the scale factor, 0.5. The new points are (0, 2.5) and (−0.5, 1.5). Draw those points and connect them to form the line. Last, find the equation of that line. Since we have the point (0, 2.5), we know the y-intercept is 2.5 or 5/2. The slope is the same as on the original line since dilated lines are parallel. Thus, the formula is y = 2x + 5/2.

6.(8, 9), (8, 27), (−1, 27)

Translate this into a math problem. This is a dilation with a scale factor of 1.5, and the center of dilation at point (−1, 9). Start with the point (5, 9). It is 6 spaces away from (−1, 9), so multiply 6 by 1.5 to get 9. The new length of that side of the kitchen is 9, so go 9 spaces to the right from (−1, 9) to get that the new point, which will be (8, 9).

Now try (−1, 21). It is 12 spaces away from the center of dilation, (−1, 9), so multiply 12 by 1.5 to get 18. The new distance is 18 spaces up from (−1, 9), so that is (−1, 27).

For the last point, the easiest way may be to refer to the previous two points. Since it’s a rectangle, the x-value must be 8 and the y-value must be 27, since this corresponds to the adjacent vertices in the figure. The third coordinate is (8, 27).

7.No

Draw the two right triangles. One has legs of 3 and 4 and the other has legs of 4 and 5. Although the 90 degree angle between them is the same, the two pairs of sides are not proportional because 4/5 is not equal to 3/4. Since the corresponding sides are not proportional, the two triangles are not similar.

8.10

Notice that the two triangles have at least one congruent angle. Compare the corresponding sides. 4.5/9 = 1/2 and 5.5/11 = 1/2, so the two sides given have the same ratio. Thus, the two triangles are similar, by the SAS similarity postulate. Side FE must be twice side CB, so it is equal to 10.

9.Not possible

The two triangles have at least one congruent angle. Examine the corresponding sides. 20 is twice 10, but 21 is not twice 9. This means the two sides provided do not have the same ratio. The triangles are not similar and therefore it is not possible to calculate the missing side without using trigonometry.

REFLECT

Congratulations on completing Chapter 3!

Here’s what we just covered.

Rate your confidence in your ability to:

•Understand and perform dilations of figures, including figures in the coordinate plane

•Identify similar triangles using the SSS, AAA, and SAS similarity postulates

If you rated any of these topics lower than you’d like, consider reviewing the corresponding lesson before moving on, especially if you found yourself unable to correctly answer one of the related end-of-chapter questions.

Access your online student tools for a handy, printable list of Key Points for this chapter. These can be helpful for retaining what you’ve learned as you continue to explore these topics.