High School Geometry Unlocked (2016)

Lesson 4.3. Problem Solving

A contractor builds a ramp to reach a loading dock that is 10 feet high. The ramp measures 26 feet along its slanted surface. What is the angle of incline of the ramp?

The ramp forms a right triangle, in which the opposite side is 10 feet and the hypotenuse is 26 feet. Since those are the two given sides, the most straightforward way to solve this problem is to calculate sin⁻¹ 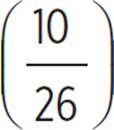, or simplify as sin⁻¹ 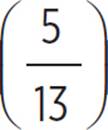. Use your calculator.

sin⁻¹ 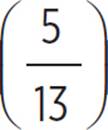≈ 22.62°

Note that you can also solve for the unknown side of this triangle, using the Pythagorean theorem.

10² + b² = 26²

100 + b² = 676

   b² = 676 − 100

   b² = 576

   b = 24

Knowing all three sides of the triangle, you can now use the other two inverse identities to solve for the same angle.

sin⁻¹ 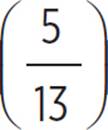≈ 22.62°

cos⁻¹ 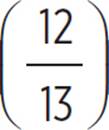≈ 22.62°

tan⁻¹ 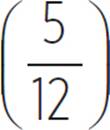≈ 22.62°

Did we need to do that here? Of course not. However, it’s helpful to know your options for more difficult problems. Some exercises in school, or on standardized tests, may challenge you to use specific functions, instead of the most straightforward one.

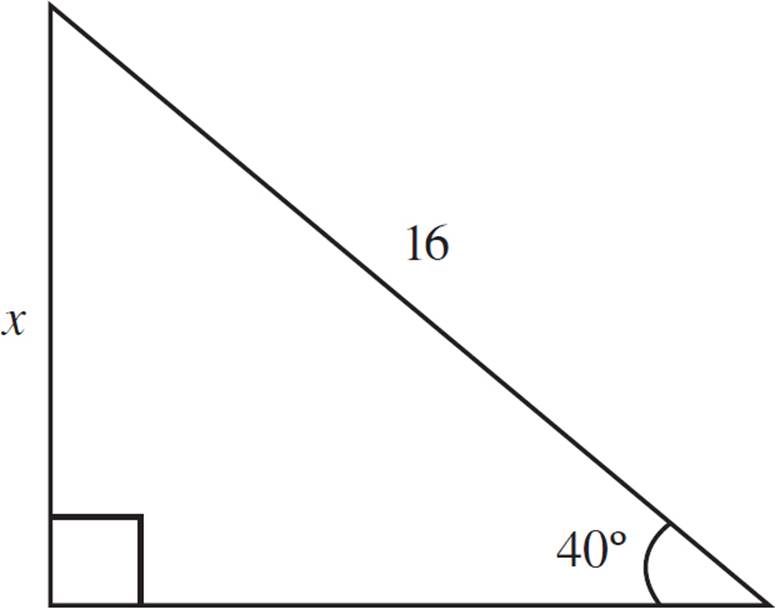
What is the value of x?

This is quite typical of the type of trig problem you might see in school, or on standardized tests. You have only one given side length, so you can’t use the Pythagorean theorem. However, you do have an angle, which allows you to use sin, cos, or tan.

To decide which function to use, consider which side length you have, and which one you need. In this case, you have the hypotenuse (16), and you need the opposite side. So, use sin(40°). Here’s how.

OTHER TRIGONOMETRIC IDENTITIES

Reciprocal Identities

The reciprocals of sine, cosine, and tangent are, respectively, cosecant (abbreviated csc), secant (abbreviated sec), and cotangent (abbreviated cot). This builds on the relationships of sin, cos, and tan, and can come in handy with more advanced problems. For now, just work on memorizing these relationships.

csc =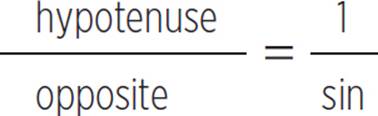

sec =

cot =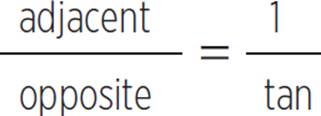

Observe the ratios in the triangle below.

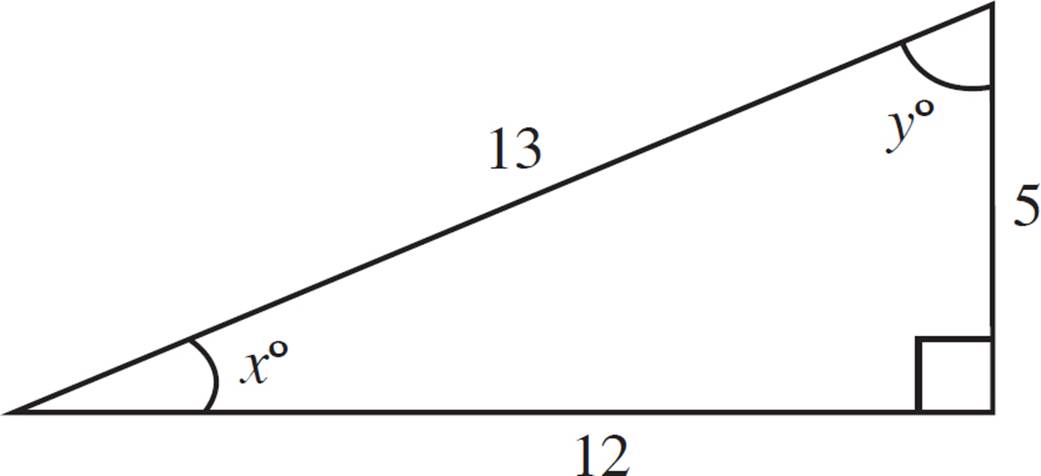
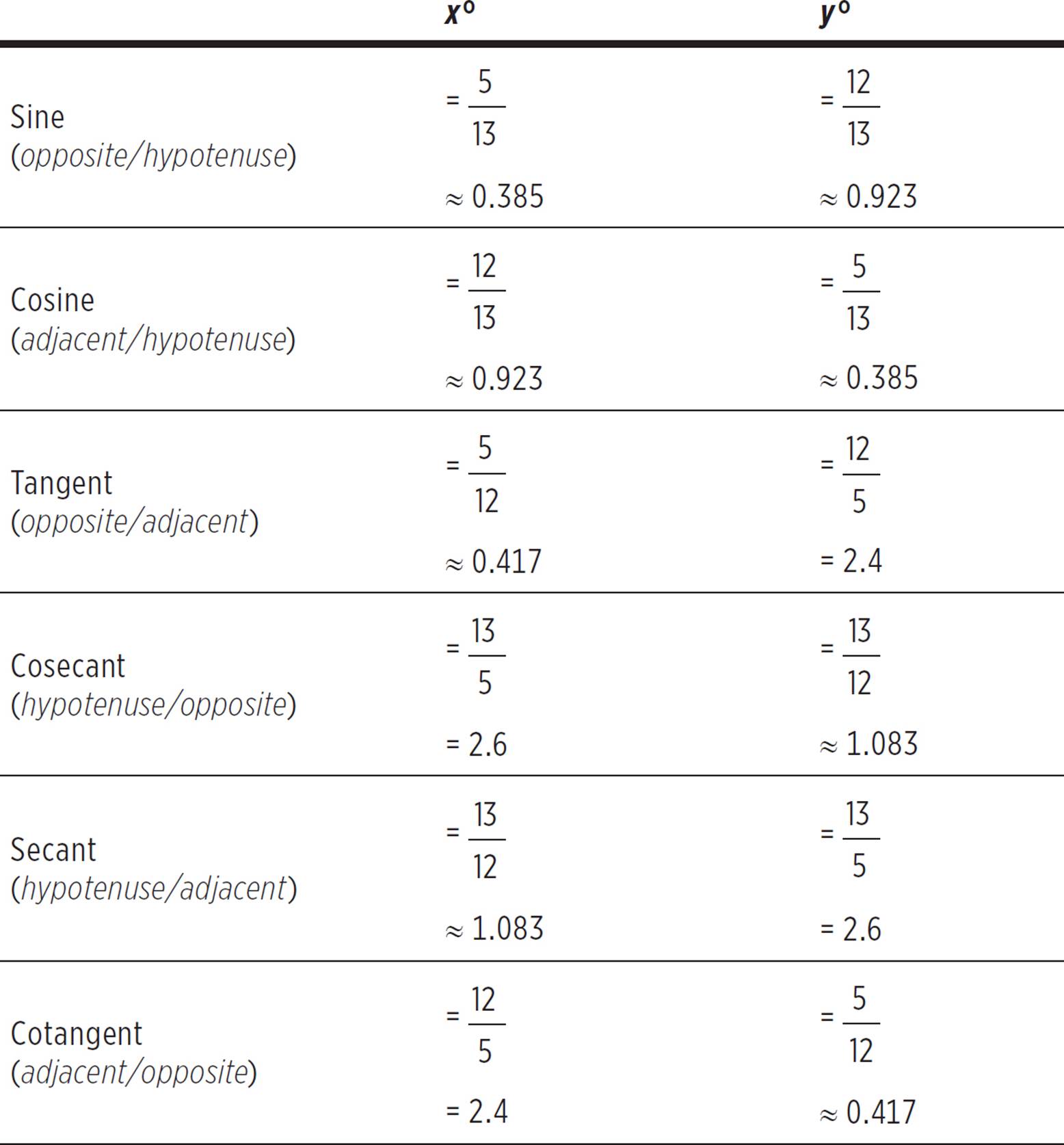
Here is how you may see reciprocal identities on the ACT.

If g(x) = sin x cot x, then which of the following trigonometric functions is equivalent to g(x)?

(Note: csc x = 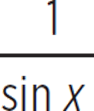, sec x = 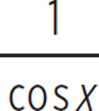, and cot x = )

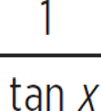A.g(x) = sin x

B.g(x) = cos x

C.g(x) = tan x

D.g(x) = csc x

E.g(x) = sec x

The Pythagorean Identity

The Pythagorean Identity is based on—you guessed it—the Pythagorean theorem. Let’s see how this is derived.

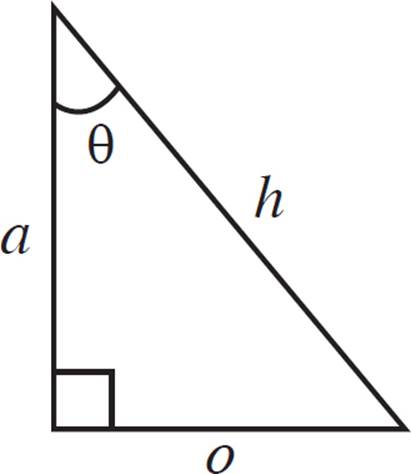
For all angles, the
value of sin and cos
is always between −1
and 1 (inclusive).

Tan does not have this
limit.

Remember: sine of x°
is written as sin(x°).

Theta (θ) is a variable
for an angle.

sin²(θ) + cos²(θ) = 1

See this in action with a 3-4-5 triangle:

An identity is an
equation or formula
that’s true for all
values.

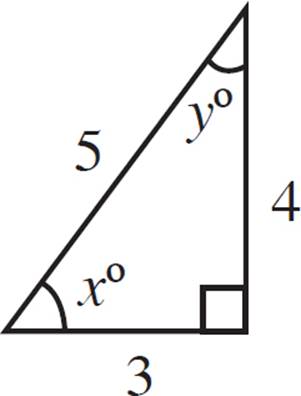
sin(x) =

cos(x) =

sin²(x) =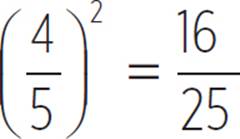

cos²(x) =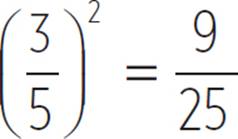

sin²(θ) + cos²(θ) =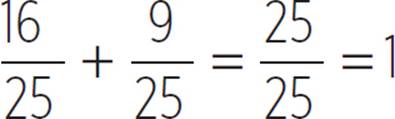

sin =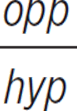

cot =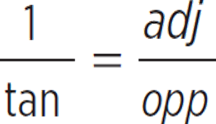

sin × cot

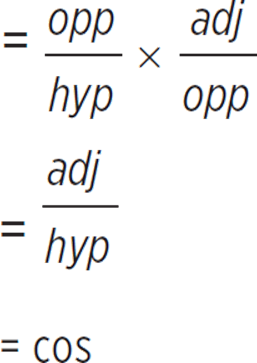    Simplify

The correct answer is (B).

Here’s another way to think about this identity.

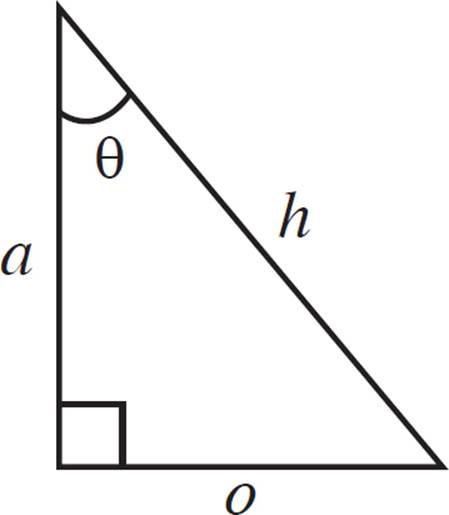
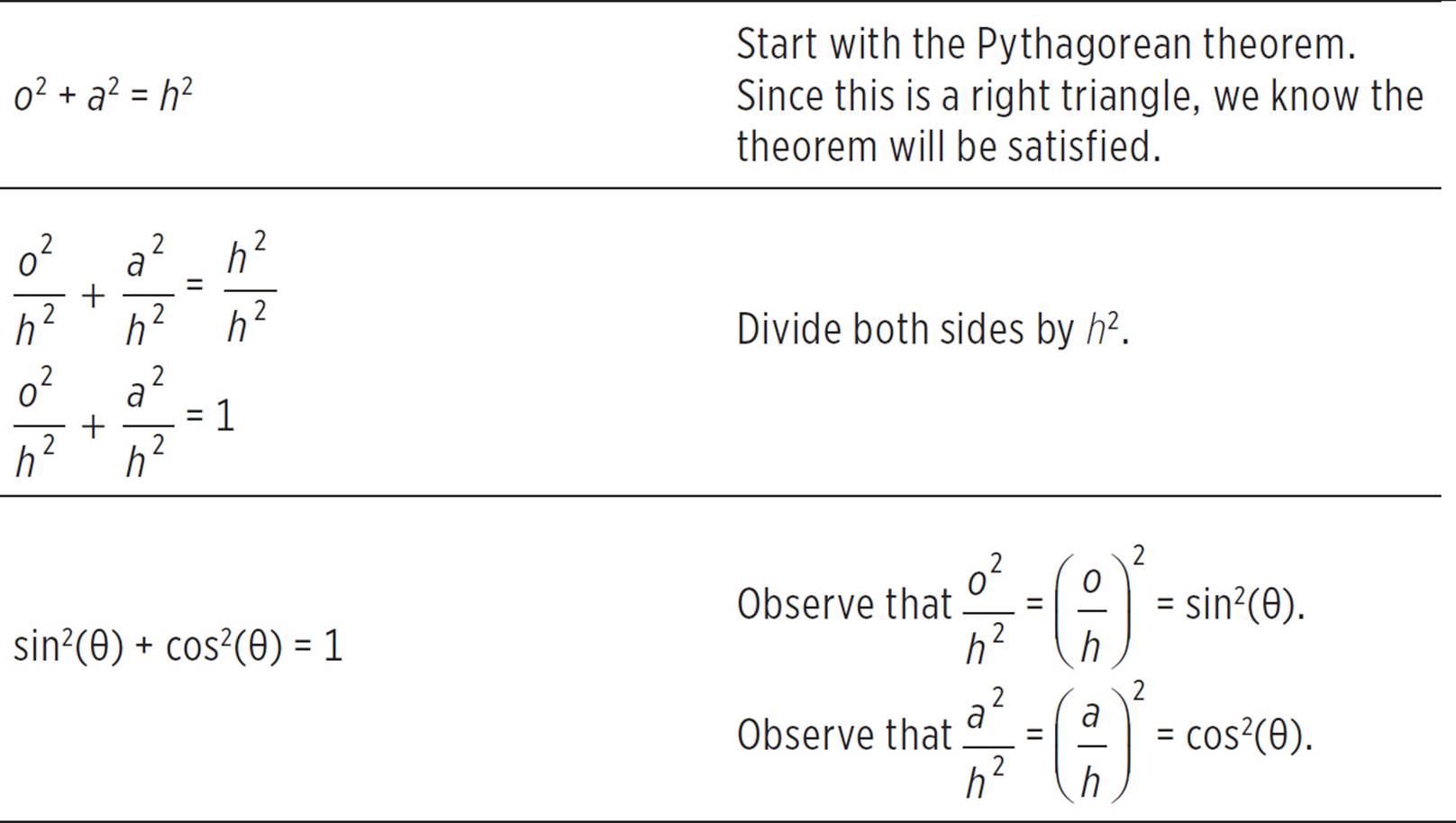
From this identity, we can derive all of the following:

sin²(θ) + cos²(θ) = 1

  1 − sin²(θ) = cos²(θ)

  1 − cos²(θ) = sin²(θ)

  tan²(θ) + 1 = sec²(θ)

  cot²(θ) + 1 = csc²(θ)

…and more!

Sin/Cos

Another very useful identity is the following:

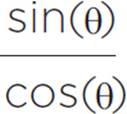= tan(θ)

Let’s see how this identity is derived.

Let’s see this identity with a 5-12-13 triangle.

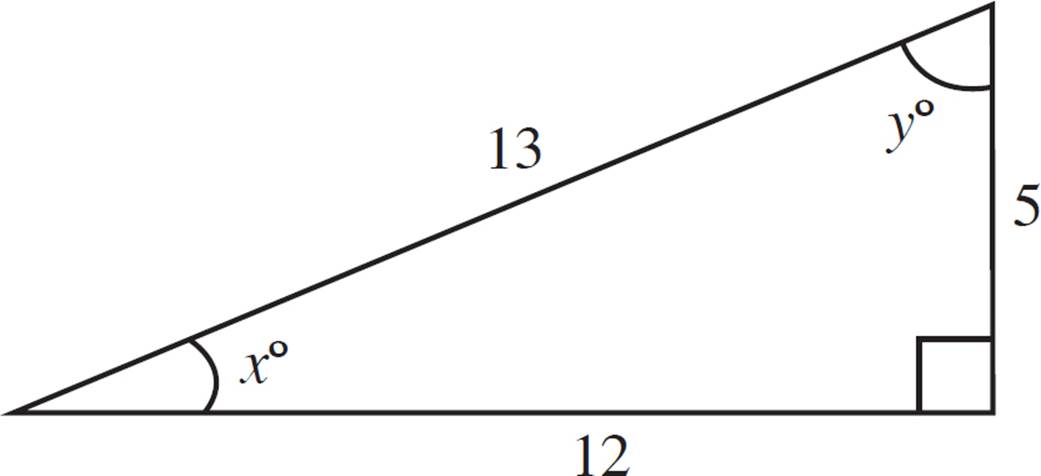
To see how
trigonometric
identities are tested on
the ACT, access your
Student Tools online.

sin(x°)/cos(x°)

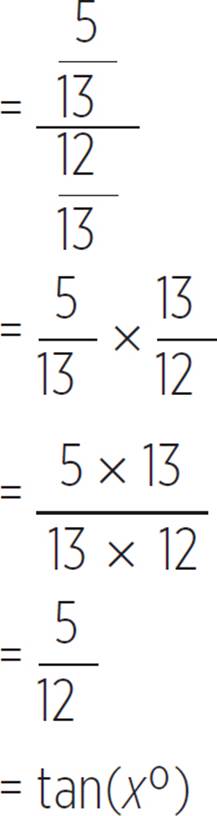
From this identity, we can derive the following:

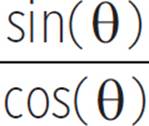= tan(θ)

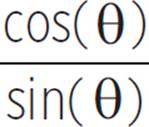= cot(θ)

…and more!