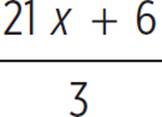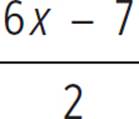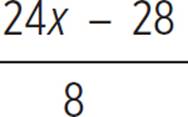High School Geometry Unlocked (2016)

GOALS

By the end of this chapter, you will be able to:

•Understand the standard form for the equation of a line

•Find an equation from a line, and plot a line from its equation

•Find the intersection of two lines

•Calculate the distance or midpoint between two coordinates

•Divide a segment to a specified ratio (e.g., 2:3 or 1:5)

•Find the vertex, roots, and axis of symmetry of a parabola

•Recognize the standard form and vertex form for the equation of a parabola

•Find the focus and directrix of a parabola from its equation

•Find the equation of a parabola given its zeroes, or its focus and directrix

•Prove geometric facts and theorems using algebra

Lesson 6.1. Algebra and the Coordinate Plane

COORDINATE GEOMETRY BASICS

Equation of a Line

Equation of a Line

y = mx + b

An equation in this form is called a linear equation, because it is guaranteed to form a straight line when graphed. The following the variables make up this equation:

•x and y are the coordinates (x, y) of a point on the line.

•m is the slope of the line (rise/run).

•b is the y-intercept of the line (the point where x = 0).

In most cases, when dealing with the equation of a line, you’ll see x and y as variables, and numerical values for m and b. Such an equation represents all the possible (x, y) coordinates that exist on a specific line. Consider this example:

y = 3x + 4

In this example, any (x, y) coordinate pair that exists on the line will satisfy the equation, and any coordinate pair that satisfies the equation will exist on the line.

The equation is a function—if you plug in a value for x, you’ll get a corresponding value for y. For instance, if we plug in x = 2, then y = 10:

y = 3(2) + 4

y = 6 + 4

y = 10

Therefore, we know that the coordinate (2, 10) exists on the line y = 3x + 4.

In coordinate geometry, you will often need to solve for one of the variables in a linear equation. For example, you might solve for slope (m) in order to find out if two lines are parallel. Or, you might solve for the x- or y-coordinate so that you can plot a point on a line.

The coordinate (2, 5) lies on the line with the equation y = 3x + b. What is the value of b?

In this example, there is only one unknown variable, b. If you plug in x = 2 and y = 5 (from the given coordinate), you can solve:

 y = 3x + b

 5 = 3(2) + b

 5 = 6 + b

5 − 6 = b

−1 = b

Find a Line from an Equation

To graph a line, you just need to plot two points, and then connect them. You can find points that lie on a line by choosing different values for x and then evaluating for y, or vice versa.

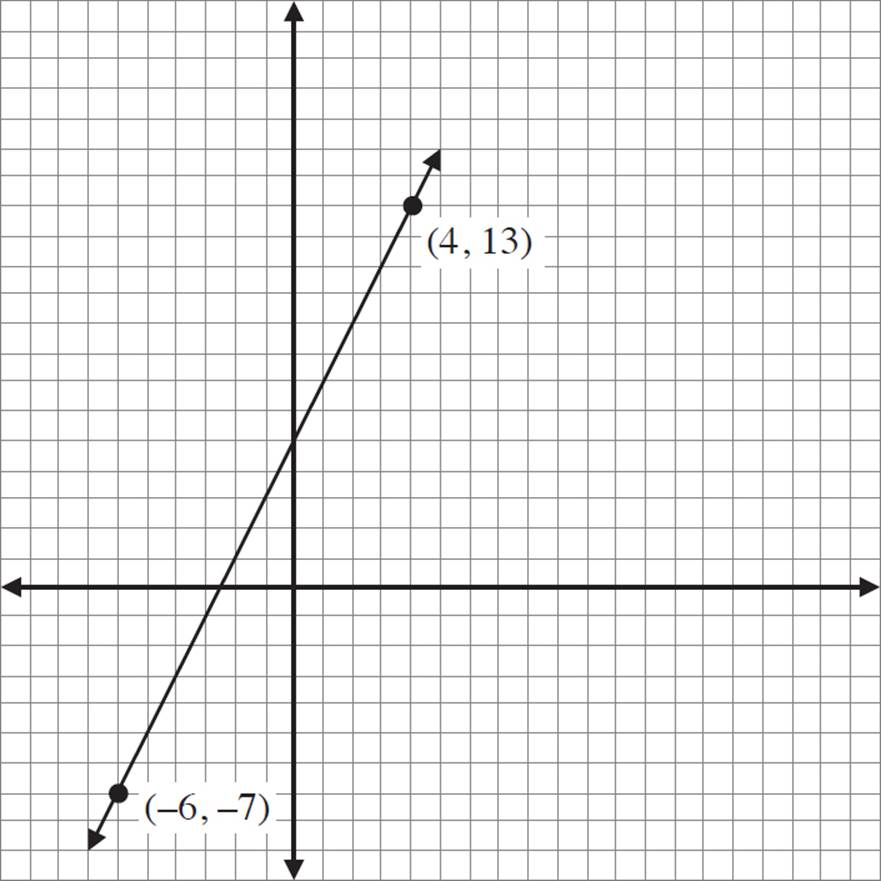
Graph the line represented by the equation y = 2x + 5.

Begin by finding a coordinate pair that satisfies the equation. To find a coordinate pair, choose a value for x and then evaluate for y. Any value will do! Try to choose numbers that make the math easy.

If you plug in x = 4, then you get y = 13.

y = 2x + 5

y = 2(4) + 5

y = 8 + 5

y = 13

Therefore, the coordinate (4, 13) lies on the line.

Now, you just need one more coordinate pair to make a line. Again, any value will do. Try x = −6.

y = 2x + 5

y = 2(−6) + 5

y = −12 + 5

y = −7

Therefore, the coordinate (−6, −7) lies on the line.

Finally, plot the two points, and connect them to make a line.

Supplies

If you’re graphing with
pencil and paper, it’s
usually a good idea
to make your two
points far apart if you
can. This will help
make your drawing
more accurate.

Find an Equation from a Line

To derive an equation from a line, you can start by choosing any two points from the line. With two points, you can then solve for m and b.

The coordinate (3, −4) and (−3, 10) both lie on the line with the equation y = mx + b. What is the value of b?

First, plug in the two coordinate pairs to make two equations:

y = mx + b

−4 = m(3) + b

10 = m(−3) + b

Then, evaluate as a system of equations. One method is to add the two equations together and see if one of the variables cancels out.

Another method is to use the slope formula to solve for m first and then solve for b.

Slope Formula

To find the slope of a line containing the points (x₁, y₁) and (x₂, y₂):

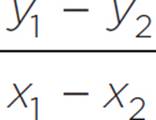
Plug in the points (3, −4) and (−3, 10) to solve for slope:

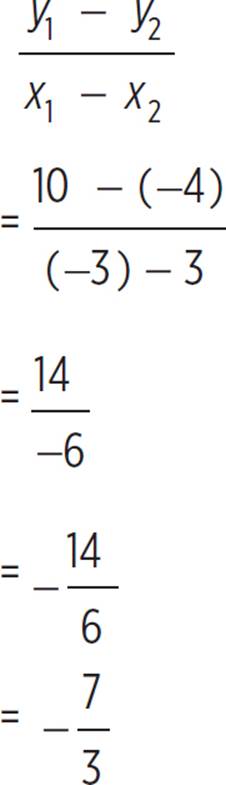
Therefore, m = − . Plug that back into the equation:

y = mx + b

y = −x + b

Finally, plug in one of the given coordinate pairs for x and y, and solve for b:

 y = −x + b

 −4 = − × 3 + b

 −4 = −7 + b

−4 + 7 = b

 3 = b

Remember to keep
your coordinates in
the same order for the
top and bottom of the
fraction, or else you’ll
get the wrong sign.

Find the Intersection of Two Lines

If two lines intersect, they do so at a single point. To find that point, you can solve as a system of two equations.

Find the intersection of (y = 4x − 3) and (y = 2x + 5).

In Example 3, we solved a system of equations by adding the equations together. Another method for solving systems is called substitution—using an equivalent expression for a certain variable, so that you can solve for another variable.

If each of the equations has y alone, that makes it easy, because we can just set the expressions as equal to each other. We know that y = y, so the two expressions are also equal to each other.

y = 4x − 3

y = 2x + 5

4x − 3 = 2x + 5

Now the y variables are gone, and we are able to solve for x.

We now have a value for x, but we still need y. Plug in x = 4 to either one of the original equations, and evaluate for y.

y = 4x − 3

y = 4 × 4 − 3

y = 16 − 3

y = 13

Here is how you may see the equation of a line on the ACT.

Quadrant(s) of the standard (x, y) coordinate plane

The line with equation 5y − 4x = 20 does NOT lie in which quadrant(s) of the standard (x, y) coordinate plane below?

A.Quadrant I only

B.Quadrant II only

C.Quadrant III only

D.Quadrant IV only

E.Quadrants I and III only

Therefore, the intersection point is (4, 13).

Intersection points should always satisfy both equations, so you can check your work by plugging the coordinate pair into the other equation:

Parallel Lines

In the standard coordinate plane, line l is represented by the equation y + 9 = 7x, and line m is represented by the equation 3y = 21x + 6. Find the intersection, if any, of lines l and m.

Whenever you have a linear equation that’s not already in the form of y = mx + b, a good first step is to put the equation in that form. This makes the equations much easier to compare.

For the first equation, y has a term added to it. To get y by itself, subtract 9 from both sides of the equation:

For the second equation, y has a coefficient. To get y by itself, divide both sides of the equation by 3:

Now, try setting the expressions equal to each other:

If you subtract 7x from both equations, you get −9 = 2, which is obviously not a true equation. In other words, there is no value for y that can equal both quantities (7x − 9) and (7x + 2). This means that there is no solution for this pair of equations—no (x, y) coordinate pair that satisfies both equations.

If a pair of linear equations has no solution, that means that the two lines do not intersect at any point. And we know that when two lines do not intersect, it means that the lines are parallel. This is an algebraic explanation for the slopes of parallel lines being equal. For example, (2x + 4) can’t possibly have a value equal to (2x + 9); therefore, we know that the pair of equations (y = 2x + 4) and (y = 2x + 9) has no solutions.

Slopes of Parallel Lines

If two lines are parallel, then they have the same slope, but different y-intercepts.

If two lines have the same slope, but different y-intercepts, then they are parallel.

Sometimes, you’ll find that two equations are actually the same.

Determine the solutions, if any, for the lines (2y = 6x − 7) and (8y + 28 = 24x).

First, put both equations into the form of y = mx + b:

First, manipulate the equation given to get y = x + 4. Then graph this line, with a slope of and a y-intercept of 4. The graph lies in the first, second, and third quadrants, and not in the fourth quadrant, (D)—the correct answer.

Therefore, these two equations actually represent the same line. If you graph both equations, they overlap each other entirely. The two equations have an infinite number of solutions.

Here is how you may see intersections of lines on the SAT.

Line m contains the points (4, 16) and (0, 8). At what point will line m intersect with line n if the equation of line n is −8x + 4y = 24?

A.(0, 0)

B.(−4, 0)

C.These lines do not intersect.

D.These lines intersect at an infinite number of points.