High School Geometry Unlocked (2016)

Lesson 8.2. Equation of a Circle

We know that the definition of a circle is “the set of points that are equidistant from a given center point.” To express a circle as an equation, we can use the Pythagorean theorem or the distance formula.

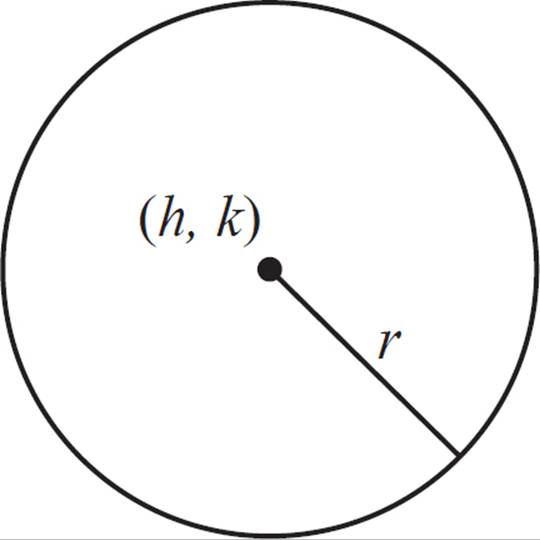
In this figure, the center of the circle is (h, k), and the radius is r. We know that for every point on the circle, the radius will always be equal to r. In other words, if (x, y) is any point on the circumference of the circle, then the distance between (x, y) and (h, k) will always be equal to r.

We know how to calculate distance using the Pythagorean theorem. If the distance from (x, y) to (h, k) were represented as a right triangle, like the one below, then we could say that a² + b² = r².

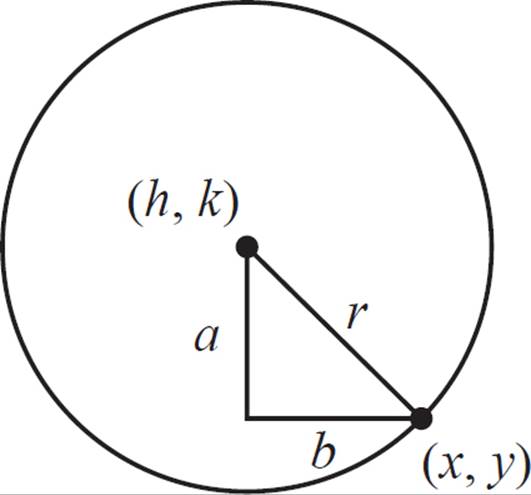
The values of a and b are the distances between the x- and y-coordinates, respectively. That is, the value of a is equal to (x − h), and the value of b is equal to (y − k).

a² + b² = r²

(x − h)² + (y − k)² = r²

That sure looks familiar! The equation of a circle is the same thing as the Distance Formula.

Equation of a Circle—Standard Form

For a circle with center (h, k) and radius r:

(x − h)² + (y − k)² = r²

And of course, if the center happens to be the origin (0, 0), then the equation can be simplified:

Equation of a Circle

For a circle with center at the origin, and radius r:

x² + y² = r²

If you see an equation in the form of (x − h)² + (y − k)² = r², you’ll know immediately that it is a circle with center (h, k) and radius r.

In the equation, the constants are h, k, and r, while x and y are variables representing all the possible points on the circle. Most commonly, you’ll see the constants as numerical values and x and y as variables.

Find the equation for the circle with center (5, 4) and radius 6.

Substitute the given values into the standard equation for a circle:

(x − h)² + (y − k)² = r²

h = 5

k = 4

r = 6

(x − 5)² + (y − 4)² = 6²

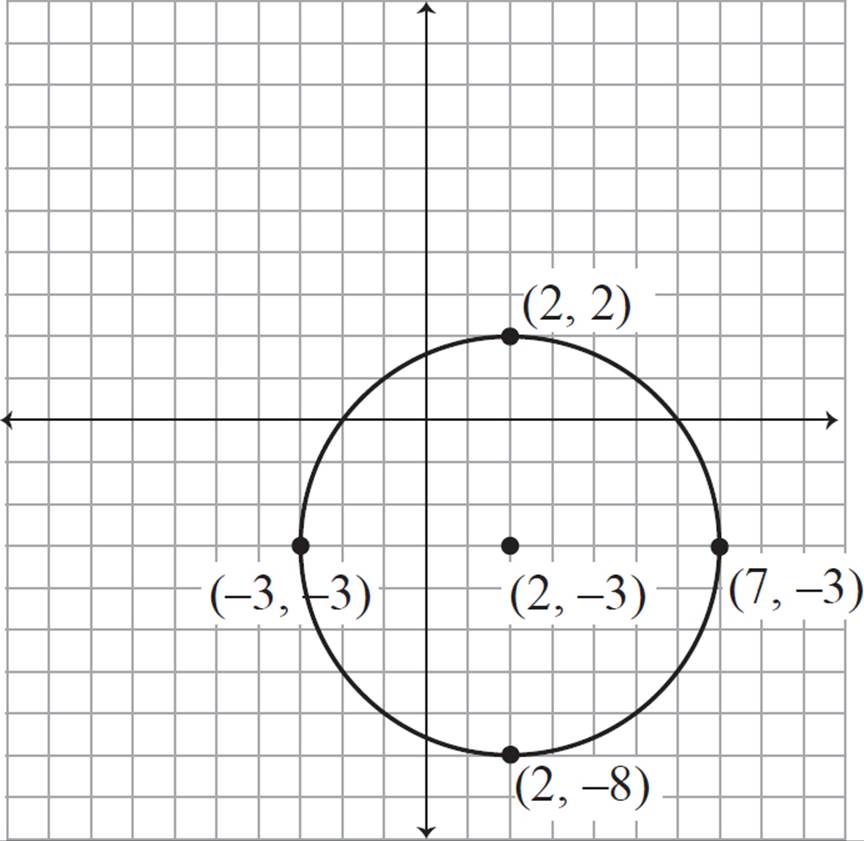
Graph the circle with the equation (x − 2)² + (y + 3)² = 5²

From the equation, you know that the center is (2, −3), and the radius is 5. Begin by plotting the center at (2, −3).

Now, the easiest points to find would be parallel to the axes—that is, directly horizontal or vertical to the center. These points can be found by counting, and you don’t need to use the equation at all.

The radius of the circle is 5. If you count from the center and move 5 units directly upward, you would find point (2, 2). This point will be on the circle, since it is exactly 5 units from the center.

Similarly, if you count 5 units down from the center, you would find point (2, −8).

5 units to the left of the center would be point (−3, −3).

5 units to the right of the center would be point (7, −3).

Plot these four points:

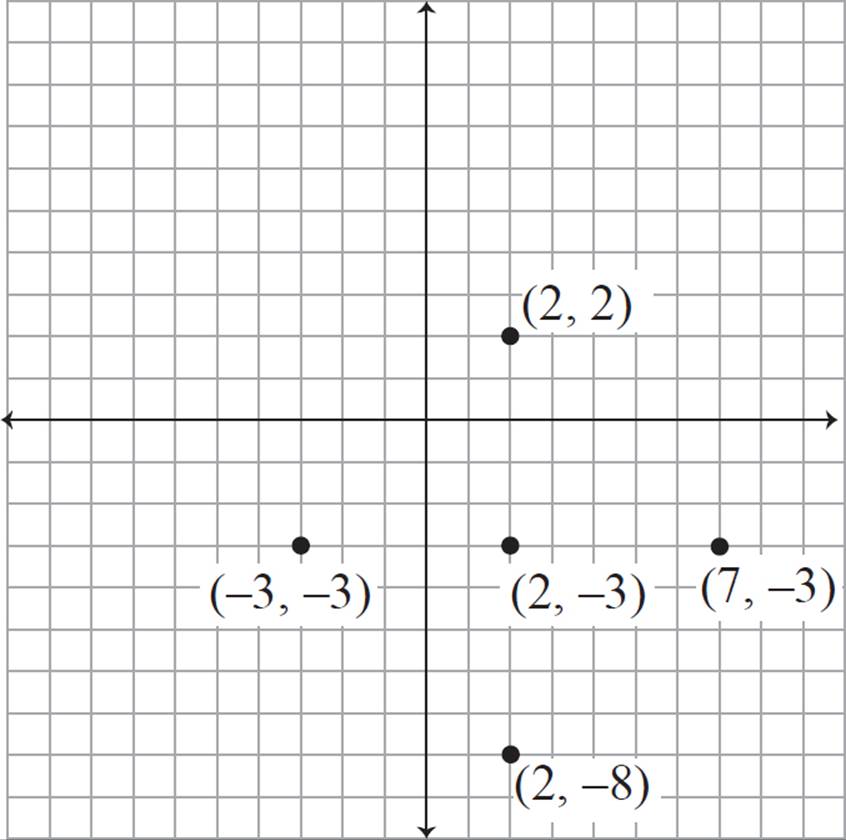
Then, connect the points with a smooth curve to make a circle. You could also use your compass.

Here is how you may see the equation of a circle on the ACT.

Which of the following equations represents the graph of a circle with center (2, −6) and radius 4 coordinate units in the standard (x, y) coordinate plane?

F.(x − 2)² + (y + 6)² = 4

G.(x + 2)² + (y − 6)² = 4

H.(x − 2)² + (y − 6)² = 16

J.(x − 2)² + (y + 6)² = 16

K.(x + 2)² + (y − 6)² = 16

Fun fact: If there happens to be a Pythagorean triple that works with your radius, then you can also find eight more integer coordinates that lie on the circle rather easily. For example, the radius in this exercise is 5. Remember that 3-4-5 is a Pythagorean triple, or in other words, 3² + 4² = 5². That means that we can add and subtract different combinations of 3 and 4 to the center coordinates to find more points on the circle.

For example, if you count from the center (2, −3) and move right 3, up 4, then you find point (5, 1). This point is on the circle because it has a distance of 5 from the center.

You can also move right 4, up 3, and find point (6, 0). This point is also 5 units from the center, and it lies on the circle.

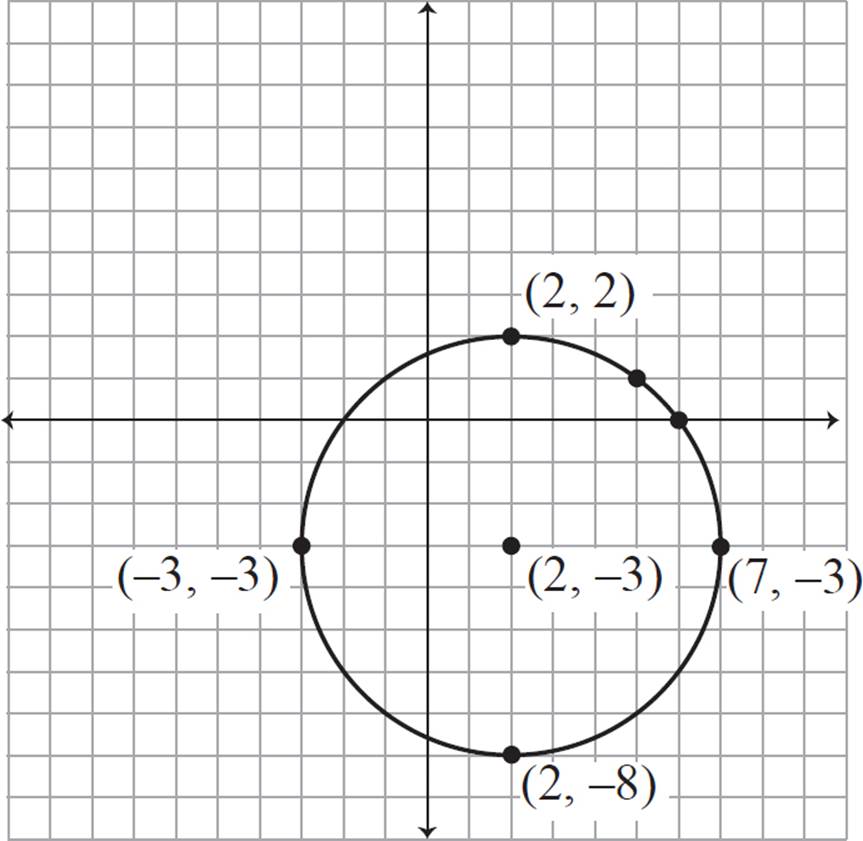
Here are all the integer coordinates that you can find in a similar manner for this circle:

(2 + 3, −3 + 4) = (5, 1)

(2 + 4, −3 + 3) = (6, 0)

(2 + 3, −3 − 4) = (5, −7)

(2 + 4, −3 − 3) = (6, −6)

(2 − 3, −3 + 4) = (−1, 1)

(2 − 4, −3 + 3) = (−2, 0)

(2 − 3, −3 − 4) = (−1, −7)

(2 − 4, −3 − 3) = (−2, −6)

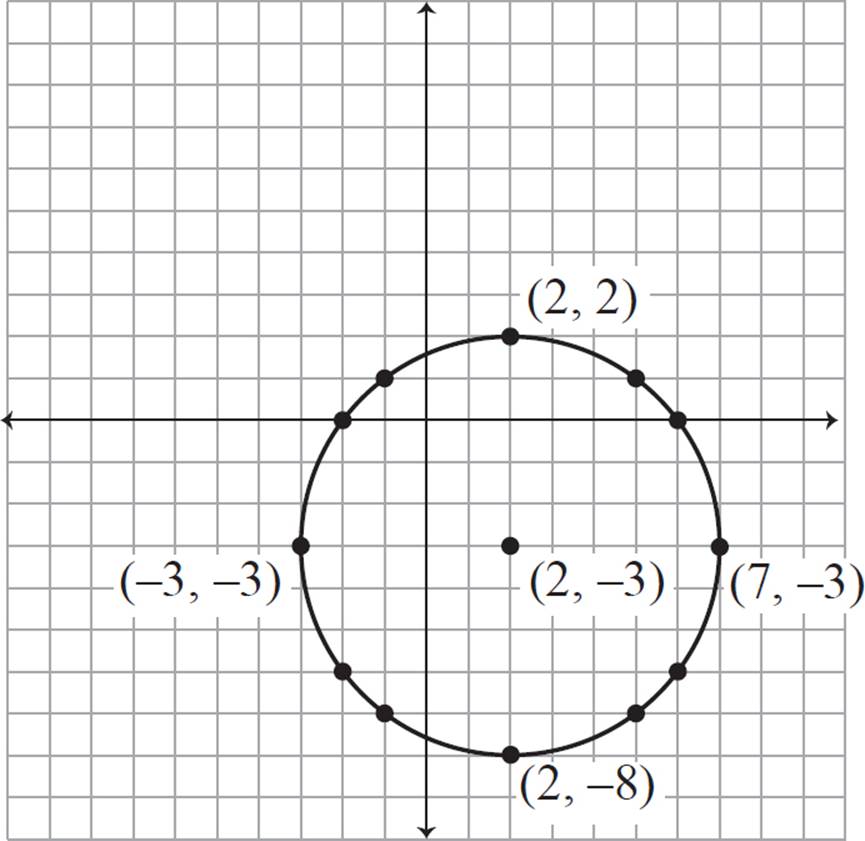
The rest of the coordinates won’t be integer pairs. But you can find any other coordinate on the circle by choosing a value for x and solving for y, or vice versa, using the equation of a circle.

Sometimes, an equation will be given in expanded form, instead of the standard (factored) form (x − h)² + (y − k)² = r².

For example, the expanded form of (x − h)² is x² − 2hx + h², and the expanded form of (y − k)² is y² − 2ky + k².

So the full, expanded form of the equation might look like this:

x² − 2hx + h² + y² − 2ky + k² = r²

The circle formula is (x − h)² + (y − k)² − r², where (h, k) is the center of the circle and r is the radius. Use Process of Elimination. Choices (F) and (G) can be eliminated because they do not square the radius. Choice (K) can also be eliminated because the x-coordinate of the center is +2, so the first part of the equation should be (x − 2)², not (x + 2)². Choice (H) can be eliminated because the y-coordinate is −6, so the second part should be (y + 6)² not (y − 6)². Only (J) remains. The correct answer is (J).

With the equation in this form (with various numbers substituted for the variables), it can be difficult to spot the constants h, k, and r. So to solve these equations, we’ll factor the expanded form using a technique called “completing the square.”

For example, if you have the equation x² + 14x + 13 = 0, it might seem like it can’t be factored, since there’s no numbers that add to 13 and multiply to 14. “Completing the square” means manipulating the equation so that it can be factored in the form of (x + n)².

Remember that (x + a)² will always expand to x² + 2ax + a². Therefore, the value of 2a will always match the coefficient of your middle term. (In this example, the coefficient is 14). So, if you divide the coefficient by 2, you find a.

Here’s how to do it:

We are left with a quadratic expression in the form of x² + 14x + ___, and we need to fill in the blank. Half of 14 is 7, so the binomial factor we want is (x + 7).

This expands as (x + 7)² = x² + 14x + 49.

So we’re substituting (x² + 14x) for (x² + 14x + 49), which means we’re adding 49 to the equation. Don’t forget to add it to the right side as well!

Therefore, the solutions to this equation are x = −1 and x = −13.

When you need to factor the equation of a circle, you’re typically going to use “completing the square” twice in order to factor the x terms and the y terms separately.

Find the center and the radius of the circle with the equation x² + y² − 10x − 12y = 3.

Complete the square for the x terms:

Complete the square for the y terms:

Therefore, we’re adding 25 and 36 to both sides of the equation.

The equation is now in standard form. Therefore, h = 5, k = 6 (so the center is (5, 6)), and r = 8.