High School Geometry Unlocked (2016)
Chapter 2. Congruence and Theorems
Lesson 2.2. Putting Theorems to the Test
In this lesson, we’ll be discussing proofs—the logical steps that one can use to show that something is true. In math, that “something” may be a theorem, postulate, definition, or some other property of a figure or problem. As mentioned earlier in this chapter, most geometry courses require students to write many, many complete proofs for any topic you might think of. The reason that this is such a popular teaching topic is that it helps students gain an intuitive understanding of why things work the way that they do. After all, math (or any other subject) shouldn’t just be about memorizing facts and formulas. If you don’t understand the hows and whys behind your subject, then you’re going to struggle when the content gets hard.
This lesson is intended in part to introduce you to the idea of proofs and how they work. We won’t actually ask you to write complete proofs, as you would in school. We will, however, show you a few examples of formal proofs as well as informal ones. The more important learning to take away from this lesson is with the concepts behind the proofs—in this case, concepts surrounding triangle congruence.
In this first example, we’ll develop not a formal proof, but an explanation for a known postulate.

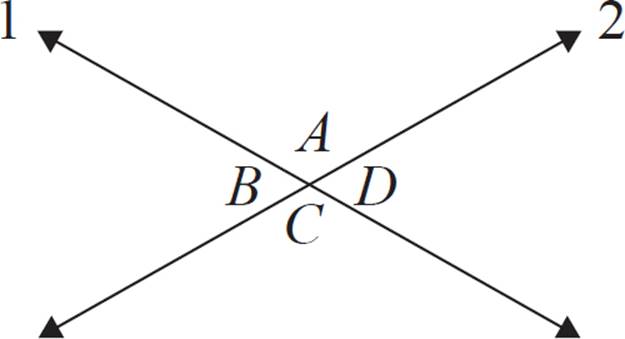
Given that 1 and 2 are lines, explain why ∠A = ∠C.
The real question here is why vertical angles are always congruent. You have probably learned the postulate that states that “vertical angles are always congruent,” but since we’re trying to explain the concept, we’re not just going to cite the postulate and call it done. Instead, we’ll find reasons to support our explanation.
First, let’s consider everything we know about this figure.
Of course, we know that both 1 and 2 are straight lines, which is a fact given in the problem. That’s important, because we know that straight lines are 180°. That means that each pair of adjacent angles in the figure has a sum of 180°. When two angles form a line as in these examples, they are called a linear pair.
Therefore,
∠A + ∠B = 180°
∠B + ∠C = 180°
∠C + ∠D = 180°
∠D + ∠A = 180°
If you look at the list of pairs above, you’ll notice equations that have an angle in common. For example, (∠A + ∠B = 180°) and (∠B + ∠C = 180°) both refer to ∠B. This allows us to use algebra skills to make some deductions.
What if we subtract ∠B in both of those two equations? Note: to make this easier to read, we’ll refer to the angles by their letters, and omit the angle symbol.
|
A + B = 180° |
|
|
A + B − B = 180° − B |
Subtract B from both sides of the equation. |
|
A = 180° − B |
|
|
B + C = 180° |
|
|
B − B + C = 180° − B |
Subtract B from both sides of the equation. |
|
C = 180° − B |
Therefore, we’ve proved that A and C are equal both equal the quantity (180° − B).


This triangular sail happens to be a version of a 5-12-13 right triangle. If you recognized the Pythagorean triple, you would know that the hypotenuse must be 130 feet long. 130 + 120 + 50 = 300 feet. You also could have used the Pythagorean theorem: a2 + b2 = c2, where a and b are the two legs of the triangle and c is the hypotenuse. Choice (B) is the correct answer.
In the following example, you’ll encounter a formal proof.

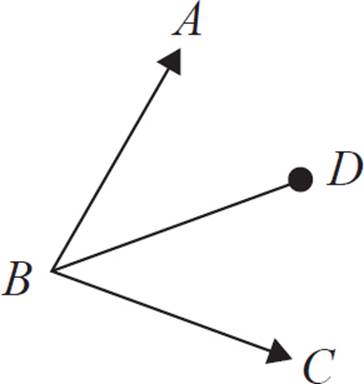
In the figure above, the measure of ∠ABC is 80°, and ∠ABC is bisected by line segment BD. What is the measure of ∠ABD?
If you were asked to explain your answer to this problem, you’d probably say something like:
“If segment BD bisects angle ABC, that means it divides the angle exactly in half. Therefore, each of the two halves must equal 40°. The measure of ∠ABD is 40°.”
If you said that, you’d be correct! However, if you were asked to write a proof for this problem, then your explanation should be different. Here’s how a proof would look for this example.
|
Given: |
∠ABC = 80° BD bisects ∠ABC |
|
Prove: |
∠ABD = 40° |
You’ll often find that there
are many possible ways
to support a particular
proof. That’s normal!
There’s rarely just one
“right” answer when
it comes to proofs.
Notice the format of this problem. In a proof exercise, you’ll often see included information labeled given, and a conclusion statement labeled prove. Your job is to document the logical steps that lead from the “given” information to the conclusion.
In writing your proof, it’s conventional to use two columns, with “Statements” on the left and “Reasons” on the right. You’ll usually begin by including some or all of the “given” information in your first statement(s). Also, if no figure has been provided, you should always draw one yourself, and label all of the given information in your figure.

Then, you would continue the proof by writing statements that can be derived from the given information. For each statement on the left, you must write your reason or justification for that statement on the right. Reasons are always general theorems or postulates—don’t use specific names from your figure in the “reasons” column.
Here’s how a complete proof might look for this example:
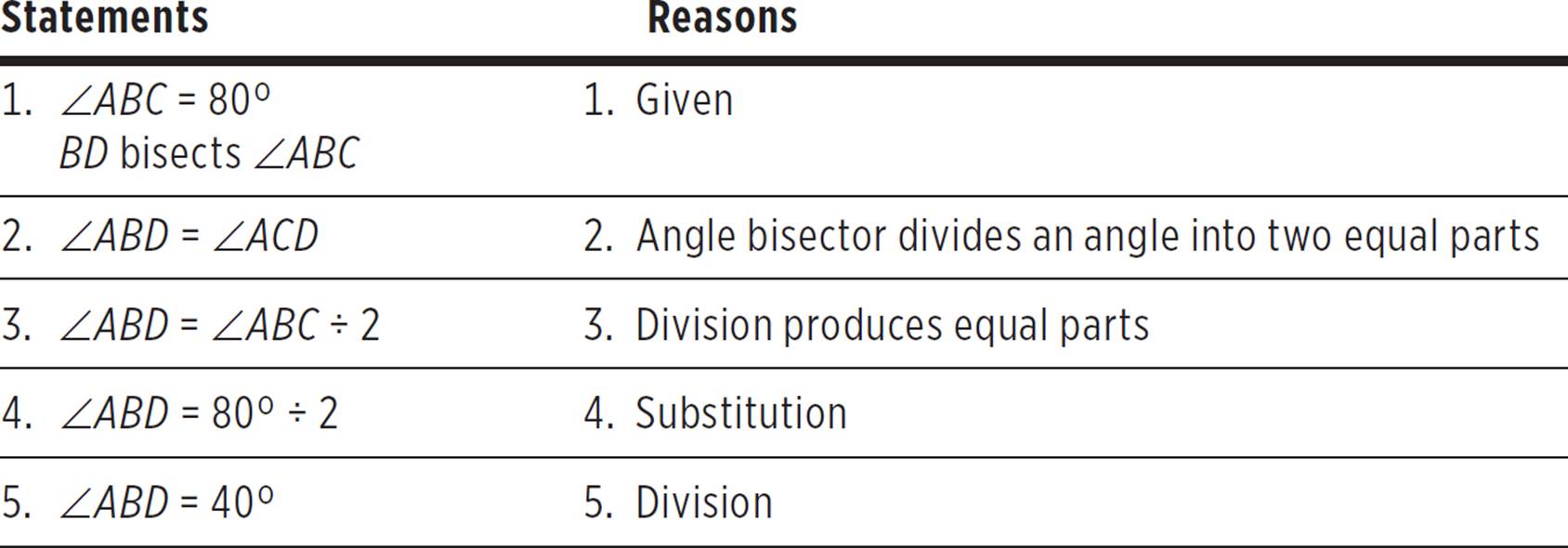

In a proof, the order of your statements can vary, as long as every statement logically follows from something above it. Additionally, you must never skip steps when writing a formal proof—if a particular fact leads to your next statement, then you must include it in writing, even if it’s very obvious. Some instructors are stricter than others when it comes to obvious steps, but it’s better to be safe than sorry. Finally, you do not need to include every possible fact about the figure in your proof—only those that are necessary and sufficient to reach the conclusion. For example, in this problem, we didn’t need to specifically mention that ∠ACD also equals 40°, even though that can be proved as well.

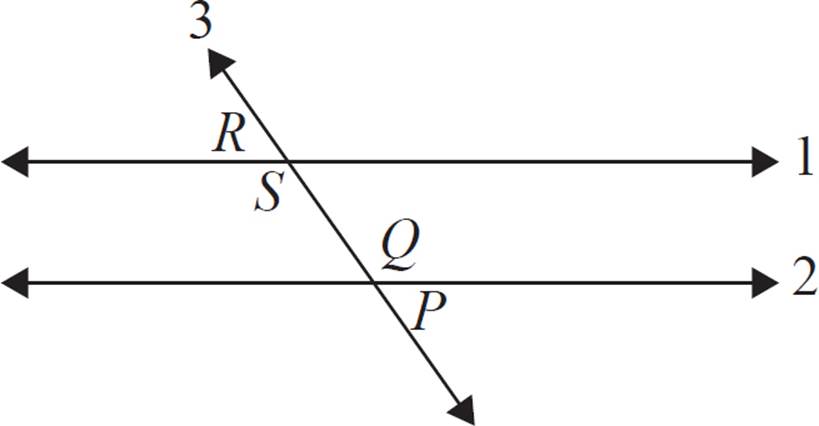
Given that 1 and 2 are parallel lines, explain why ∠P = ∠R.
In this example, we know that ∠P + ∠Q = 180°, because they form a linear pair. It’s also true that ∠R + ∠S = 180°.
Often, you’ll use
known theorems to
support your proofs. If
you’re writing a formal
proof, you can refer to
theorems by name, or
restate the theorems
themselves in your
Reasons column.
We also know that ∠Q = ∠S, because of the alternating interior angles theorem, which states that when two parallel lines are intersected by a transversal, the pairs of alternating interior angles are congruent.
|
If ∠Q = ∠S, then we can use substitution. Let’s substitute ∠Q for ∠S in one of the two linear pairs, so that ∠Q appears in both equations. |
|
|
∠P + ∠Q = 180° |
∠R + ∠S = 180° |
|
becomes |
|
|
∠P + ∠Q = 180° |
∠R + ∠Q = 180° |
|
Let’s subtract ∠Q from both equations. |
|
|
∠P = 180° − ∠Q |
∠R = 180° − ∠Q |
|
Therefore, we’ve proved that ∠P and ∠R are equal—both equal the quantity (180° − ∠Q). |
|


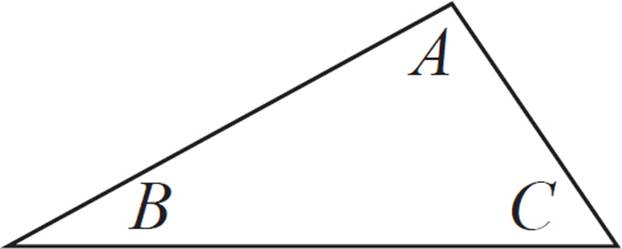
|
Given: |
A, B, and C are interior angles of a triangle. |
|
Prove: |
∠A + ∠B + ∠C = 180° |
In this example, we’ll explain why the sum of interior angles of a triangle is always 180°. One way to set this up is to draw a line that’s parallel to one of the triangle’s sides, which lets us use the alternate interior angles postulate.
Let’s draw a line through A that’s parallel to side BC. Then, we’ll extend side AB so that it forms a transversal line (shown below).
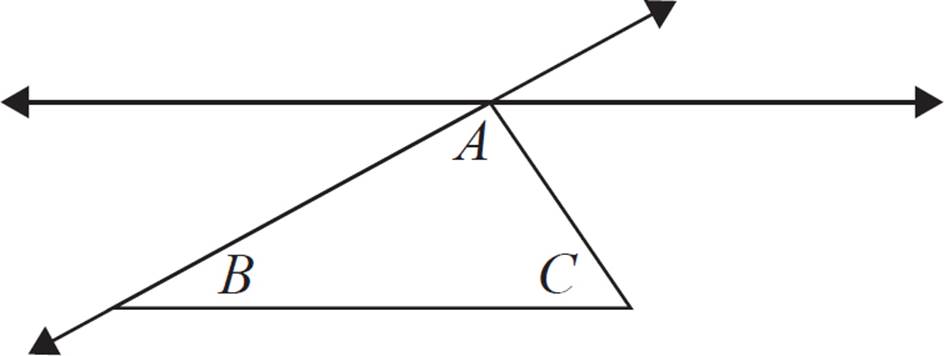
Because we’ve specified that there are two parallel lines, then we know that the alternate interior angles are congruent. Therefore, we can label the alternate interior angle that’s congruent to B.
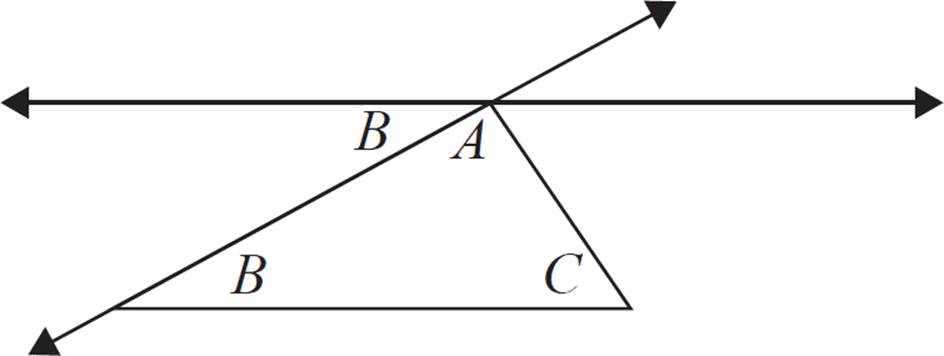
We can use the same process with the other side. Extend AC to make a transversal line. Then, we can label the alternate interior angle that’s congruent to C.
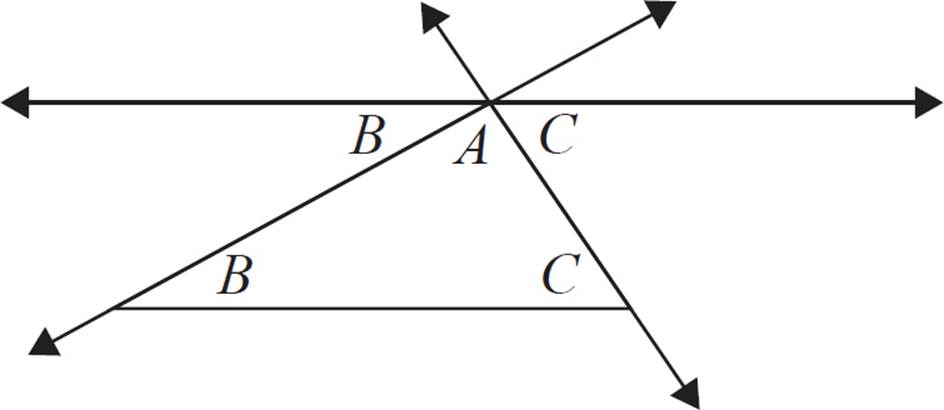
Finally, observe that angles A, B, and C form a straight angle at the top of the figure. Straight angles are always equal to 180°, so these three adjacent angles must have a sum of 180°. Therefore, ∠A + ∠B + ∠C = 180°.


Now that you’ve seen a few examples of proofs, can you identify the missing step in the proof below?

|
Given: |
A, B, C, and D are interior angles of a parallelogram. |
|
Prove: |
∠A = ∠C |
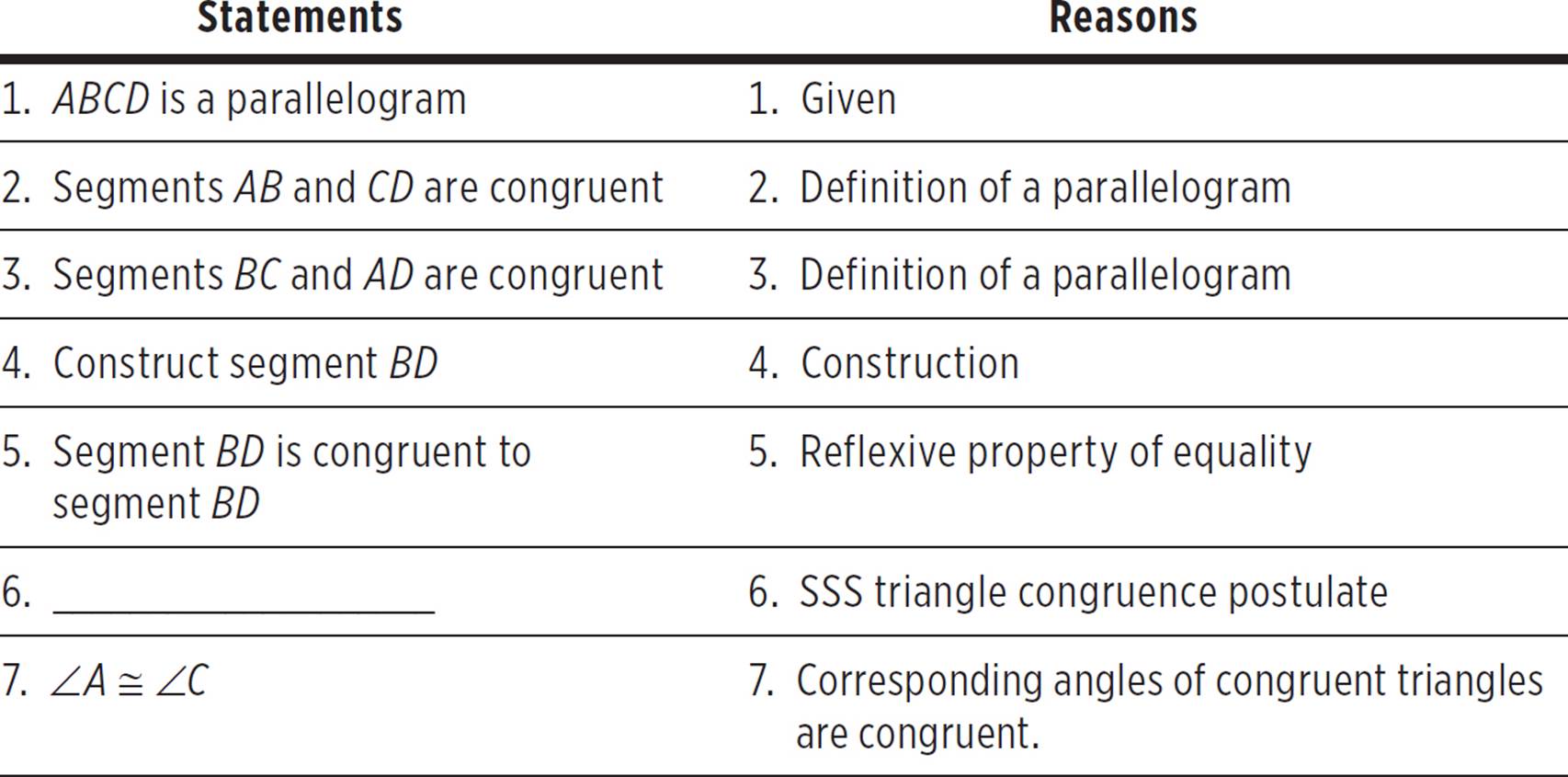
What is the missing step in the proof above? We gave you a hint in the “reasons” column—we’re using the SSS triangle congruence postulate. After constructing segment BD according to the proof, which two triangles are formed? The two triangles are ABDand BCD. (It’s fine if you named them a little differently, for example BDA for the first triangle, as long as you include the correct 3 vertices). In the previous steps of the proof, we’ve proven that the corresponding sides of those two triangles are congruent. Therefore, we can use the SSS congruence postulate to say that the two triangles are congruent.
The missing statement is “Triangles ABD and BCD are congruent.”


Which triangle congruence postulate can be used to support statement 7 in the proof below?
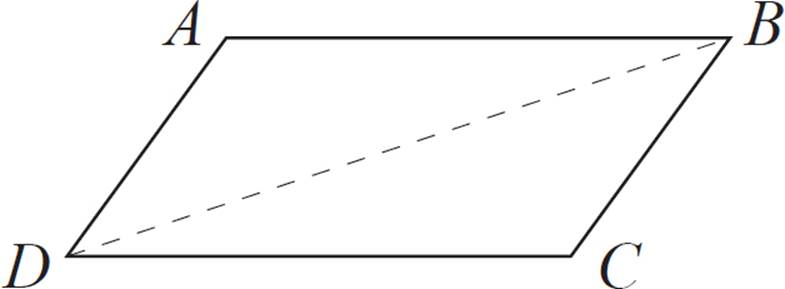
|
Given: |
ABCD is a parallelogram. |
|
Prove: |
side AB ≅ side CD |
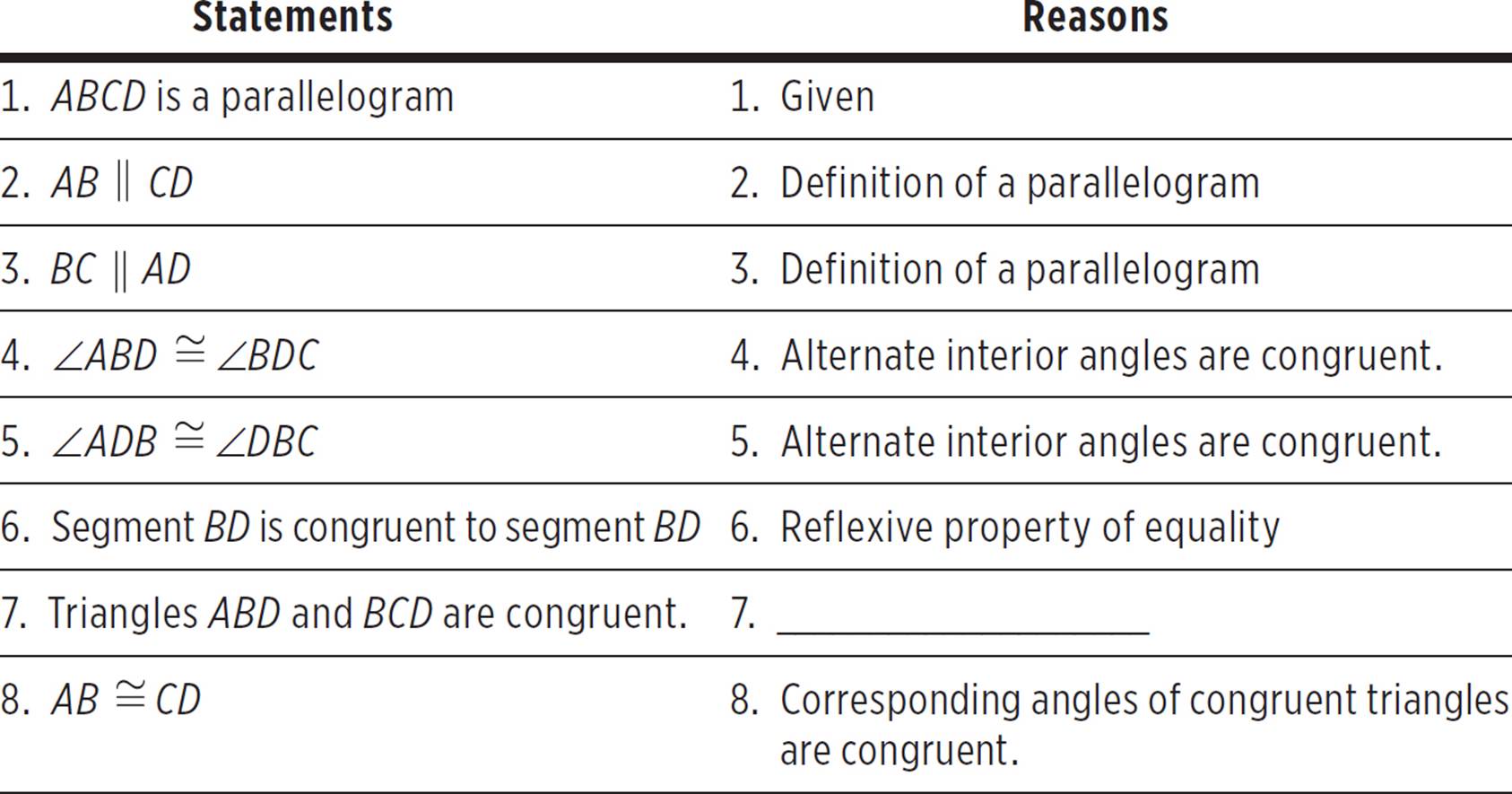
What is the support for statement 7? We’re claiming that triangles ABD and BCD are congruent. In the previous statements, we’ve shown two pairs of corresponding angles are congruent, and the side between them (BD) is congruent. The triangle congruence postulate that works here is the ASA (Angle-Side-Angle) congruence postulate.