GMAT Quantitative Review

3.0 Math Review

3.1 Arithmetic

10. Counting Methods

There are some useful methods for counting objects and sets of objects without actually listing the elements to be counted. The following principle of multiplication is fundamental to these methods.

If an object is to be chosen from a set of m objects and a second object is to be chosen from a different set of n objects, then there are mn ways of choosing both objects simultaneously.

As an example, suppose the objects are items on a menu. If a meal consists of one entree and one dessert and there are 5 entrees and 3 desserts on the menu, then there are different meals that can be ordered from the menu. As another example, each time a coin is flipped, there are two possible outcomes, heads and tails. If an experiment consists of 8 consecutive coin flips, then the experiment has 2⁸ possible outcomes, where each of these outcomes is a list of heads and tails in some order.

A symbol that is often used with the multiplication principle is the factorial. If n is an integer greater than 1, then n factorial, denoted by the symbol n!, is defined as the product of all the integers from 1 to n. Therefore,

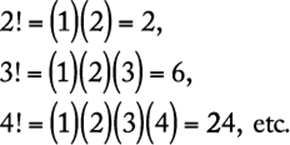
Also, by definition, .

The factorial is useful for counting the number of ways that a set of objects can be ordered. If a set of n objects is to be ordered from 1st to nth, then there are n choices for the 1st object, choices for the 2nd object, choices for the 3rd object, and so on, until there is only 1 choice for the nth object. Thus, by the multiplication principle, the number of ways of ordering the n objects is . . . .

For example, the number of ways of ordering the letters A, B, and C is 3!, or 6:

ABC, ACB, BAC, BCA, CAB, and CBA.

These orderings are called the permutations of the letters A, B, and C.

A permutation can be thought of as a selection process in which objects are selected one by one in a certain order. If the order of selection is not relevant and only k objects are to be selected from a larger set of n objects, a different counting method is employed.

Specifically, consider a set of n objects from which a complete selection of k objects is to be made without regard to order, where . Then the number of possible complete selections of k objects is called the number of combinations of n objects taken k at a time and is denoted by . The value of is given by .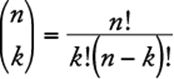

Note that is the number of k-element subsets of a set with n elements. For example, if , then the number of 2-element subsets of S, or the number of combinations of 5 letters taken 2 at a time, is .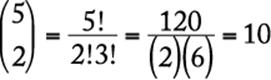

The subsets are {A, B}, {A, C}, {A, D}, {A, E}, {B, C}, {B, D}, {B, E}, {C, D}, {C, E}, and {D, E}. Note that 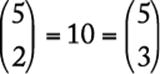because every 2-element subset chosen from a set of 5 elements corresponds to a unique 3-element subset consisting of the elements notchosen. In general, .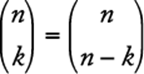