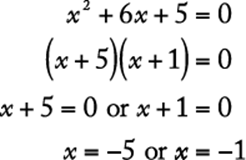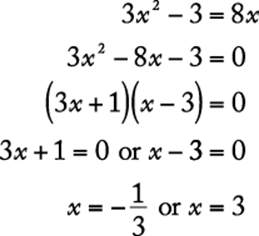GMAT Quantitative Review

3.0 Math Review

3.2 Algebra

6. Solving Quadratic Equations

The standard form for a quadratic equation is

,

where a, b, and c are real numbers and ; for example:

Some quadratic equations can easily be solved by factoring. For example:

A quadratic equation has at most two real roots and may have just one or even no real root. For example, the equation can be expressed as , or ; thus the only root is 3. The equation has no real root; since the square of any real number is greater than or equal to zero, must be greater than zero.

An expression of the form can be factored as .

For example, the quadratic equation can be solved as follows.

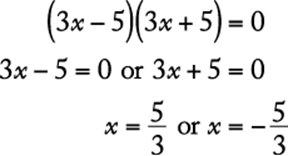
If a quadratic expression is not easily factored, then its roots can always be found using the quadratic formula: If , then the roots are

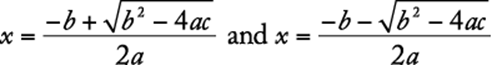
These are two distinct real numbers unless . If , then these two expressions for x are equal to 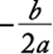, and the equation has only one root. If , then is not a real number and the equation has no real roots.