GMAT Quantitative Review

3.0 Math Review

3.2 Algebra

10. Functions

An algebraic expression in one variable can be used to define a function of that variable. A function is denoted by a letter such as f or g along with the variable in the expression. For example, the expression defines a function f that can be denoted by

.

The expression 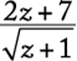defines a function g that can be denoted by

.

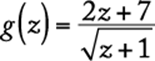The symbols “f (x)” or “g (z)” do not represent products; each is merely the symbol for an expression, and is read “f of x” or “g of z.”

Function notation provides a short way of writing the result of substituting a value for a variable. If x = 1 is substituted in the first expression, the result can be written , and is called the “value of f at .” Similarly, if is substituted in the second expression, then the value of g at is .

Once a function is defined, it is useful to think of the variable x as an input and as the corresponding output. In any function there can be no more than one output for any given input. However, more than one input can give the same output; for example, if , then .

The set of all allowable inputs for a function is called the domain of the function. For f and g defined above, the domain of f is the set of all real numbers and the domain of g is the set of all numbers greater than −1. The domain of any function can be arbitrarily specified, as in the function defined by “ for .” Without such a restriction, the domain is assumed to be all values of x that result in a real number when substituted into the function.

The domain of a function can consist of only the positive integers and possibly 0. For example, 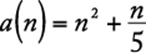for . . . .

Such a function is called a sequence and a(n) is denoted by a_n. The value of the sequence a_n at is 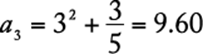. As another example, consider the sequence defined by for . . . . A sequence like this is often indicated by listing its values in the order b₁, b₂, b₃, . . . , b_n, . . . as follows:

−1, 2, −6, . . . , (−1)ⁿ(n!), . . . , and (−1)ⁿ(n!) is called the nth term of the sequence.