GMAT Quantitative Review
3.0 Math Review
3.3 Geometry
6. Triangles
There are several special types of triangles with important properties. But one property that all triangles share is that the sum of the lengths of any two of the sides is greater than the length of the third side, as illustrated below.
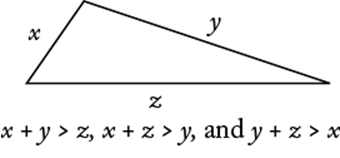
An equilateral triangle has all sides of equal length. All angles of an equilateral triangle have equal measure. An isosceles triangle has at least two sides of the same length. If two sides of a triangle have the same length, then the two angles opposite those sides have the same measure. Conversely, if two angles of a triangle have the same measure, then the sides opposite those angles have the same length. In isosceles triangle PQR below, 
since 
.
A triangle that has a right angle is a right triangle. In a right triangle, the side opposite the right angle is the hypotenuse, and the other two sides are the legs. An important theorem concerning right triangles is the Pythagorean theorem, which states: In a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the legs.
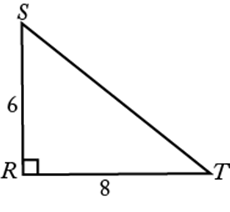
In the figure above, 
is a right triangle, so 
. Here, 
and 
, so 
, since 
and 
. Any triangle in which the lengths of the sides are in the ratio 3:4:5 is a right triangle. In general, if a, b, and c are the lengths of the sides of a triangle and 
, then the triangle is a right triangle.
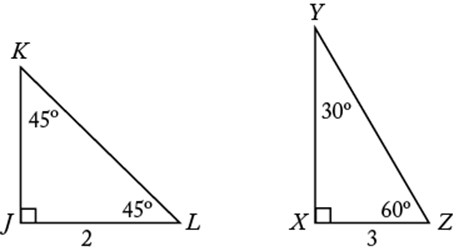
In 
triangles, the lengths of the sides are in the ratio 
. For example, in 
, if 
, then 
and 
. In 
triangles, the lengths of the sides are in the ratio 
. For example, in 
, if 
, then 
and 
.
The altitude of a triangle is the segment drawn from a vertex perpendicular to the side opposite that vertex. Relative to that vertex and altitude, the opposite side is called the base.
The area of a triangle is equal to:
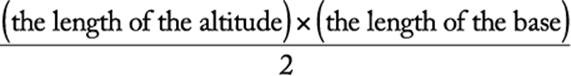
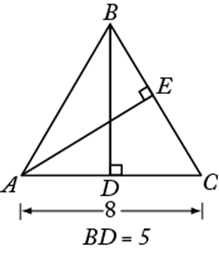
In 
, 
is the altitude to base 
and 
is the altitude to base 
. The area of is equal to
.
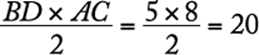The area is also equal to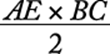 
. If 
above is isosceles and 
, then altitude 
bisects the base; that is, 
. Similarly, any altitude of an equilateral triangle bisects the side to which it is drawn.
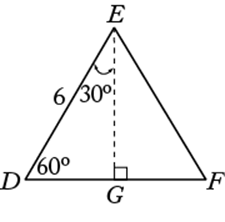
In equilateral triangle DEF, if 
, then 
and 
. The area of 
is equal to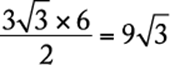 
.