GMAT Quantitative Review
3.0 Math Review
3.3 Geometry
10. Coordinate Geometry
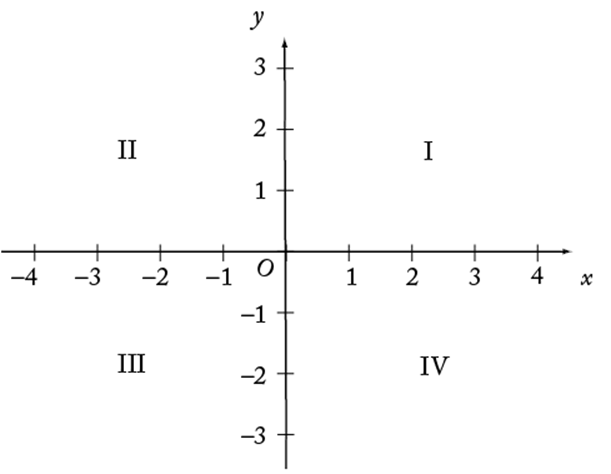
The figure above shows the (rectangular) coordinate plane. The horizontal line is called the x-axis and the perpendicular vertical line is called the y-axis. The point at which these two axes intersect, designated O, is called the origin. The axes divide the plane into four quadrants, I, II, III, and IV, as shown.
Each point in the plane has an x-coordinate and a y-coordinate. A point is identified by an ordered pair (x,y) of numbers in which the x-coordinate is the first number and the y-coordinate is the second number.

In the graph above, the (x,y) coordinates of point P are (2,3) since P is 2 units to the right of the y-axis (that is, ![]() ) and 3 units above the x-axis (that is,
) and 3 units above the x-axis (that is, ![]() ). Similarly, the (x,y) coordinates of point Q are (−4,−3). The origin O has coordinates (0,0).
). Similarly, the (x,y) coordinates of point Q are (−4,−3). The origin O has coordinates (0,0).
One way to find the distance between two points in the coordinate plane is to use the Pythagorean theorem.

To find the distance between points R and S using the Pythagorean theorem, draw the triangle as shown. Note that Z has (x,y) coordinates (−2,−3), ![]() , and
, and ![]() . Therefore, the distance between R and S is equal to
. Therefore, the distance between R and S is equal to
![]() .
.
For a line in the coordinate plane, the coordinates of each point on the line satisfy a linear equation of the form ![]() (or the form
(or the form ![]() if the line is vertical). For example, each point on the line on the next page satisfies the equation
if the line is vertical). For example, each point on the line on the next page satisfies the equation 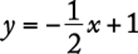 . One can verify this for the points (−2,2), (2,0), and (0,1) by substituting the respective coordinates for x and y in the equation.
. One can verify this for the points (−2,2), (2,0), and (0,1) by substituting the respective coordinates for x and y in the equation.

In the equation ![]() of a line, the coefficient m is the slope of the line and the constant term b is the y-intercept of the line. For any two points on the line, the slope is defined to be the ratio of the difference in the y-coordinates to the difference in the x-coordinates. Using (−2, 2) and (2, 0) above, the slope is
of a line, the coefficient m is the slope of the line and the constant term b is the y-intercept of the line. For any two points on the line, the slope is defined to be the ratio of the difference in the y-coordinates to the difference in the x-coordinates. Using (−2, 2) and (2, 0) above, the slope is
 .
.
The y-intercept is the y-coordinate of the point at which the line intersects the y-axis. For the line above, the y-intercept is 1, and this is the resulting value of y when x is set equal to 0 in the equation 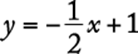 . The x-intercept is the x-coordinate of the point at which the line intersects the x-axis. The x-intercept can be found by setting
. The x-intercept is the x-coordinate of the point at which the line intersects the x-axis. The x-intercept can be found by setting ![]() and solving for x. For the line
and solving for x. For the line 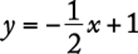 , this gives
, this gives
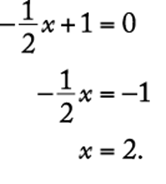
Thus, the x-intercept is 2.
Given any two points (x1,y1) and (x2,y2) with ![]() , the equation of the line passing through these points can be found by applying the definition of slope. Since the slope is
, the equation of the line passing through these points can be found by applying the definition of slope. Since the slope is 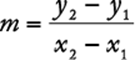 , then using a point known to be on the line, say (x1,y1), any point (x,y) on the line must satisfy
, then using a point known to be on the line, say (x1,y1), any point (x,y) on the line must satisfy 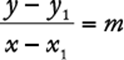 , or
, or ![]() . (Using (x2,y2) as the known point would yield an equivalent equation.) For example, consider the points (−2,4) and (3,−3) on the line below.
. (Using (x2,y2) as the known point would yield an equivalent equation.) For example, consider the points (−2,4) and (3,−3) on the line below.

The slope of this line is 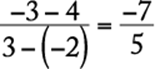 , so an equation of this line can be found using the point (3,−3) as follows:
, so an equation of this line can be found using the point (3,−3) as follows:
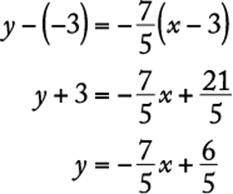
The y-intercept is ![]() . The x-intercept can be found as follows:
. The x-intercept can be found as follows:
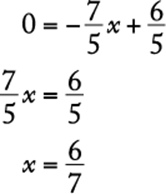
Both of these intercepts can be seen on the graph.
If the slope of a line is negative, the line slants downward from left to right; if the slope is positive, the line slants upward. If the slope is 0, the line is horizontal; the equation of such a line is of the form ![]() since
since ![]() . For a vertical line, slope is not defined, and the equation is of the form
. For a vertical line, slope is not defined, and the equation is of the form ![]() , where a is the x-intercept.
, where a is the x-intercept.
There is a connection between graphs of lines in the coordinate plane and solutions of two linear equations with two unknowns. If two linear equations with unknowns x and y have a unique solution, then the graphs of the equations are two lines that intersect in one point, which is the solution. If the equations are equivalent, then they represent the same line with infinitely many points or solutions. If the equations have no solution, then they represent parallel lines, which do not intersect.
There is also a connection between functions (see section 3.2.10) and the coordinate plane. If a function is graphed in the coordinate plane, the function can be understood in different and useful ways. Consider the function defined by
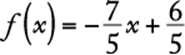 .
.
If the value of the function, f (x), is equated with the variable y, then the graph of the function in the xy-coordinate plane is simply the graph of the equation
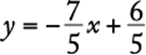
shown above. Similarly, any function f (x) can be graphed by equating y with the value of the function:
![]() .
.
So for any x in the domain of the function f, the point with coordinates (x, f (x)) is on the graph of f, and the graph consists entirely of these points.
As another example, consider a quadratic polynomial function defined by ![]() . One can plot several points (x, f (x)) on the graph to understand the connection between a function and its graph:
. One can plot several points (x, f (x)) on the graph to understand the connection between a function and its graph:
|
x |
f(x) |
|
−2 |
3 |
|
−1 |
0 |
|
0 |
−1 |
|
1 |
0 |
|
2 |
3 |
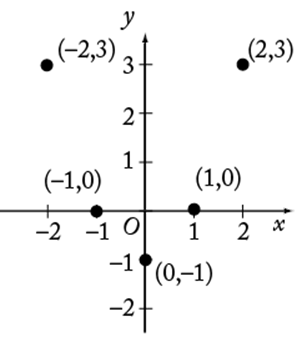
If all the points were graphed for ![]() , then the graph would appear as follows.
, then the graph would appear as follows.
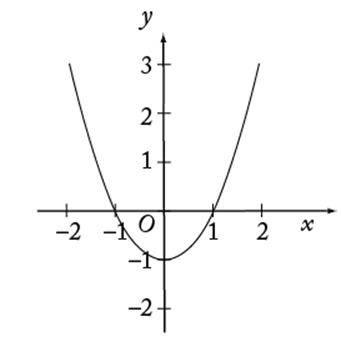
The graph of a quadratic function is called a parabola and always has the shape of the curve above, although it may be upside down or have a greater or lesser width. Note that the roots of the equation ![]() are
are ![]() and
and ![]() ; these coincide with the x-intercepts since x-intercepts are found by setting
; these coincide with the x-intercepts since x-intercepts are found by setting ![]() and solving for x. Also, the y-intercept is
and solving for x. Also, the y-intercept is ![]() because this is the value of y corresponding to
because this is the value of y corresponding to ![]() . For any function f, the x-intercepts are the solutions of the equation
. For any function f, the x-intercepts are the solutions of the equation ![]() and they-intercept is the value f (0).
and they-intercept is the value f (0).