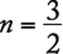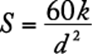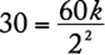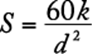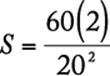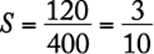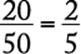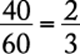GMAT Quantitative Review
4.0 Problem Solving
4.5 Answer Explanations
The following discussion is intended to familiarize you with the most efficient and effective approaches to the kinds of problems common to problem solving questions. The particular questions in this chapter are generally representative of the kinds of problem solving questions you will encounter on the GMAT. Remember that it is the problem solving strategy that is important, not the specific details of a particular question.
1. Points A, B, C, and D, in that order, lie on a line. If AB = 3 cm, AC = 4 cm, and BD = 6 cm, what is CD, in centimeters?
1. (A) 1
2. (B) 2
3. (C) 3
4. (D) 4
5. (E) 5
Geometry Lines and segments
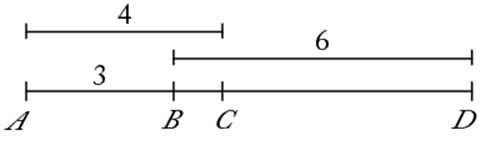
The figure shows points A, B, C, and D as well as the given measurements. Since AC = AB +BC, it follows that 4 = 3 + BC, and so BC = 1. Then, since BD = BC + CD, it follows that 6 = 1 + CD, and so CD = 5.
Alternately, AD = AB + BD = 3 + 6 = 9. Also, AD = AC + CD, so 9 = 4 + CD and CD = 5.
The correct answer is E.
2. What is the value of x2yz − xyz2, if x = −2, y = 1, and z = 3?
1. (A) 20
2. (B) 24
3. (C) 30
4. (D) 32
5. (E) 48
Algebra Operations on integers
Given that x = −2, y = 1, and z = 3, it follows by substitution that
|
x2yz − xyz2 |
= |
(−2)2(1)(3) − (−2)(1)(32) |
|
= |
(4)(1)(3) − (−2)(1)(9) |
|
|
= |
12 − (−18) |
|
|
= |
12 + 18 |
|
|
= |
30 |
The correct answer is C.
3. If x > y and y > z, which of the following represents the greatest number?
1. (A) x − z
2. (B) x − y
3. (C) y − x
4. (D) z − y
5. (E) z − x
Algebra Inequalities
From x > y and y > z, it follows that x > z. These inequalities imply the following about the differences that are given in the answer choices:
|
Answer choice |
Difference |
Algebraic sign |
Reason |
|
(A) |
x − z |
positive |
x > z implies x − z > 0 |
|
(B) |
x − y |
positive |
x > y implies x − y > 0 |
|
(C) |
y − x |
negative |
x − y > 0 implies y − x < 0 |
|
(D) |
z − y |
negative |
y > z implies 0 > z − y |
|
(E) |
z − x |
negative |
x − z > 0 implies z − x < 0 |
Since the expressions in A and B represent positive numbers and the expressions in C, D, and E represent negative numbers, the latter can be eliminated because every negative number is less than every positive number. To determine which of x − z and x − y is greater, consider the placement of points with coordinates x, y, and z on the number line.
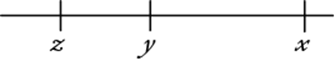
The distance between x and z (that is, x − z) is the sum of the distance between x and y (that is, x − y) and the distance between y and z (that is, y − z). Therefore, (x − z) > (x − y), which means that x − z represents the greater of the numbers represented by (x − z) and (x − y). Thus, x − z represents the greatest of the numbers represented by the answer choices.
Alternatively,
|
y > z |
given |
|
-y < − z |
multiply both sides by −1 |
|
x − y < x − z |
add x to both sides |
Thus, x − z represents the greater of the numbers represented by (x − z) and (x − y). Therefore, x − z represents the greatest of the numbers represented by the answer choices.
The correct answer is A.
4. To order certain plants from a catalog, it costs $3.00 per plant, plus a 5 percent sales tax, plus $6.95 for shipping and handling regardless of the number of plants ordered. If Company C ordered these plants from the catalog at the total cost of $69.95, how many plants did Company C order?
1. (A) 22
2. (B) 21
3. (C) 20
4. (D) 19
5. (E) 18
Algebra First-degree equations
Letting x represent the number of plants Company C bought from the catalog, then, in dollars, 3.00x is the cost of the plants, (0.05)(3.00x) is the sales tax, and 6.95 is the shipping and handling fee. It follows that
|
3.00x + (0.05)(3.00x) + 6.95 = 69.95 |
plants + tax + shipping = total |
|
(3.00x)(1.05) + 6.95 = 69.95 |
add like terms |
|
(3.00x)(1.05) = 63.00 |
subtract 6.95 from both sides |
|
x = 20 |
divide both sides by (3.00)(1.05) |
Therefore, Company C bought 20 plants from the catalog.
The correct answer is C.
5. Company C produces toy trucks at a cost of $5.00 each for the first 100 trucks and $3.50 for each additional truck. If 500 toy trucks were produced by Company C and sold for $10.00 each, what was Company C”s gross profit?
1. (A) $2,250
2. (B) $2,500
3. (C) $3,100
4. (D) $3,250
5. (E) $3,500
Arithmetic Applied problems
The company”s gross profit on the 500 toy trucks is the company”s revenue from selling the trucks minus the company”s cost of producing the trucks. The revenue is (500)($10.00) = $5,000. The cost for the first 100 trucks is (100)($5.00) = $500, and the cost for the other 400 trucks is (400)($3.50) = $1,400 for a total cost of $500 + $1,400 = $1,900. Thus, the company”s gross profit is $5,000 − $1,900 = $3,100.
The correct answer is C.
6. A group of store managers must assemble 280 displays for an upcoming sale. If they assemble 25 percent of the displays during the first hour and 40 percent of the remaining displays during the second hour, how many of the displays will not have been assembled by the end of the second hour?
1. (A) 70
2. (B) 98
3. (C) 126
4. (D) 168
5. (E) 182
Arithmetic Percents
If, during the first hour, 25 percent of the total displays were assembled, then ![]() displays were assembled, leaving
displays were assembled, leaving ![]() displays remaining to be assembled. Since 40 percent of the remaining displays were assembled during the second hour,
displays remaining to be assembled. Since 40 percent of the remaining displays were assembled during the second hour, ![]() displays were assembled during the second hour. Thus,
displays were assembled during the second hour. Thus, ![]() displays were assembled during the first two hours and
displays were assembled during the first two hours and ![]() displays had not been assembled by the end of the second hour.
displays had not been assembled by the end of the second hour.
The correct answer is C.
7. Of the following, which is least?
1. A. 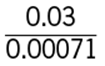
2. B. 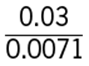
3. C. 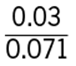
4. D. 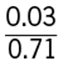
5. E. 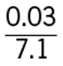
Arithmetic Operations on rational numbers
Since the numerator of all of the fractions in the answer choices is 0.03, the least of the fractions will be the fraction with the greatest denominator. The greatest denominator is 7.1, and so the least of the fractions is 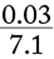 .
.
The correct answer is E.
8. The maximum recommended pulse rate R, when exercising, for a person who is x years of age is given by the equation ![]() . What is the age, in years, of a person whose maximum recommended pulse rate when exercising is 140?
. What is the age, in years, of a person whose maximum recommended pulse rate when exercising is 140?
1. (A) 40
2. (B) 45
3. (C) 50
4. (D) 55
5. (E) 60
Algebra Substitution; Operations with rational numbers
Substitute 140 for R in the given equation and solve for x.
![]()
![]()
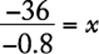
![]()
The correct answer is B.
9. There are five sales agents in a certain real estate office. One month Andy sold twice as many properties as Ellen, Bob sold 3 more than Ellen, Cary sold twice as many as Bob, and Dora sold as many as Bob and Ellen together. Who sold the most properties that month?
1. (A) Andy
2. (B) Bob
3. (C) Cary
4. (D) Dora
5. (E) Ellen
Algebra Order
Let x represent the number of properties that Ellen sold, where x ≥ 0. Then, since Andy sold twice as many properties as Ellen, 2x represents the number of properties that Andy sold. Bob sold 3 more properties than Ellen, so (x + 3) represents the number of properties that Bob sold. Cary sold twice as many properties as Bob, so 2(x + 3) = (2x + 6) represents the number of properties that Cary sold. Finally, Dora sold as many properties as Bob and Ellen combined, so [(x + 3) + x] = (2x + 3) represents the number ofproperties that Dora sold. The following table summarizes these results.
|
Agent |
Properties sold |
|
Andy |
2x |
|
Bob |
x + 3 |
|
Cary |
2x + 6 |
|
Dora |
2x + 3 |
|
Ellen |
x |
Since x ≥ 0, clearly 2x + 6 exceeds x, x + 3, 2x, and 2x + 3. Therefore, Cary sold the most properties.
The correct answer is C.
10. Which of the following represent positive numbers?
I. −3 − (−5)
II. (−3)(−5)
III. −5 − (−3)
1. (A) I only
2. (B) II only
3. (C) III only
4. (D) I and II
5. (E) II and III
Arithmetic Operations on integers
Find the value of each expression to determine if it is positive.
I. −3 − (−5) = −3 + 5 = 2, which is positive.
II. (−3)(−5) = 15, which is positive.
III. −5 − (−3) = −5 + 3 = −2, which is not positive.
The correct answer is D.
11. If ![]() is 2 more than
is 2 more than ![]() , then
, then ![]()
1. (A) 4
2. (B) 8
3. (C) 16
4. (D) 32
5. (E) 64
Algebra First-degree equations
Write an equation for the given information and solve for x.
![]()
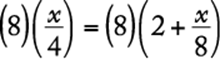
![]()
![]()
The correct answer is C.
12. If Mario was 32 years old 8 years ago, how old was he x years ago?
1. (A) ![]()
2. (B) ![]()
3. (C) ![]()
4. (D) ![]()
5. (E) ![]()
Arithmetic Operations on rational numbers
Since Mario was 32 years old 8 years ago, his age now is ![]() years old. Therefore, x years ago Mario was
years old. Therefore, x years ago Mario was ![]() years old.
years old.
The correct answer is C.
13. The toll T, in dollars, for a truck using a certain bridge is given by the formula T = 1.50 + 0.50(x − 2), where x is the number of axles on the truck. What is the toll for an 18-wheel truck that has 2 wheels on its front axle and 4 wheels on each of its other axles?
1. (A) $2.50
2. (B) $3.00
3. (C) $3.50
4. (D) $4.00
5. (E) $5.00
Algebra Operations on rational numbers
The 18-wheel truck has 2 wheels on its front axle and 4 wheels on each of its other axles, and so if A represents the number of axles on the truck in addition to the front axle, then 2 + 4A = 18, from which it follows that 4A = 16 and A = 4.
Therefore, the total number of axles on the truck is 1 + A = 1 + 4 = 5. Then, using T = 1.50 + 0.50(x − 2), where x is the number of axles on the truck and x = 5, it follows that T = 1.50 + 0.50(5 − 2) = 1.50 + 1.50 = 3.00. Therefore, the toll for the truck is $3.00.
The correct answer is B.
14. If 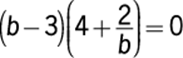 and
and ![]() , then
, then ![]()
1. (A) −8
2. (B) −2
3. (C) ![]()
4. (D) ![]()
5. (E) 2
Algebra Second-degree equations
If 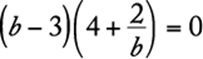 , then
, then ![]() or
or 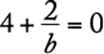 . Since
. Since ![]() , then
, then ![]() and so
and so 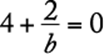 . Solve for b.
. Solve for b.
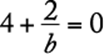
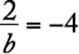
![]()
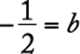
The correct answer is C.
15. For what value of x between −4 and 4, inclusive, is the value of x2 − 10x + 16 the greatest?
1. (A) −4
2. (B) −2
3. (C) 0
4. (D) 2
5. (E) 4
Algebra Second-degree equations
Given the expression x2 − 10x + 16, a table of values can be created for the corresponding function f(x) = x2 − 10x + 16 and the graph in the standard (x,y) coordinate plane can be sketched by plotting selected points:
|
x |
f(x) |
|
-4 |
72 |
|
-3 |
55 |
|
-2 |
40 |
|
-1 |
27 |
|
0 |
16 |
|
1 |
7 |
|
2 |
0 |
|
3 |
-5 |
|
4 |
-8 |
|
5 |
-9 |
|
6 |
-8 |
|
7 |
-5 |
|
8 |
0 |
|
9 |
7 |
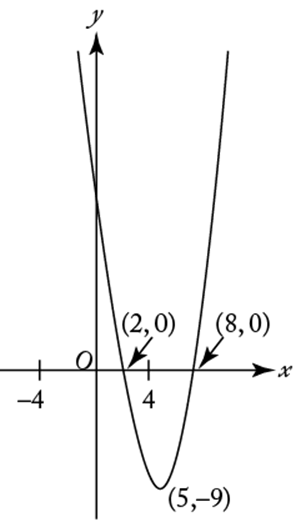
It is clear from both the table of values and the sketch of the graph that as the value of x increases from −4 to 4, the values of x2 − 10x + 16 decrease. Therefore, the value of x2 − 10x + 16 is greatest when x = −4.
Alternatively, the given expression, x2 − 10x + 16, has the form ax2 + bx + c, where a = 1, b = −10, and c = 16. The graph in the standard (x,y) coordinate plane of the corresponding function f(x) = ax2 + bx + c is a parabola with vertex at x = − ![]() , and so the vertex of the graph of f(x) = x2 − 10x + 16 is at x = −
, and so the vertex of the graph of f(x) = x2 − 10x + 16 is at x = − 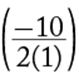 = 5.
= 5.
Because a = 1 and 1 is positive, this parabola opens upward and values of x2 − 10x + 16 decrease as x increases from −4 to 4. Therefore, the greatest value of x2 − 10x + 16 for all values of x between −4 and 4, inclusive, is at x = −4.
The correct answer is A.
16. The number ![]() is how many times the number
is how many times the number ![]() ?
?
1. (A) 2
2. (B) 2.5
3. (C) 3
4. (D) 3.5
5. (E) 4
Arithmetic Operations on rational numbers
Set up an equation in the order given in the problem, and solve for x.
![]()
![]()
![]()
The correct answer is C.
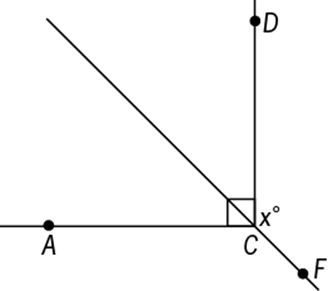
17. In the figure above, if F is a point on the line that bisects angle ACD and the measure of angle DCF is ![]() , which of the following is true of x?
, which of the following is true of x?
1. (A) ![]()
2. (B) ![]()
3. (C) ![]()
4. (D) ![]()
5. (E) ![]()
Geometry Angles
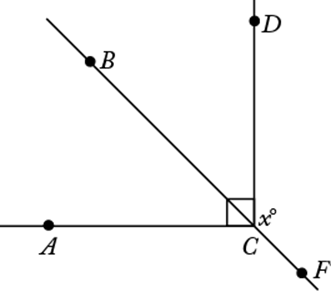
As shown in the figure above, if B is on the line that bisects ![]() , then the degree measure of
, then the degree measure of ![]() is
is 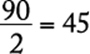 . Then because B, C, and F are collinear, the sum of the degree measures of
. Then because B, C, and F are collinear, the sum of the degree measures of ![]() and
and ![]() is 180. Therefore,
is 180. Therefore, ![]() and 130 ≤ 135 < 140.
and 130 ≤ 135 < 140.
The correct answer is E.
18. In which of the following pairs are the two numbers reciprocals of each other?
I. 3 and ![]()
II. ![]() and
and ![]()
III. ![]() and
and ![]()
1. (A) I only
2. (B) II only
3. (C) I and II
4. (D) I and III
5. (E) II and III
Arithmetic Properties of numbers (reciprocals)
Two numbers are reciprocals of each other if and only if their product is 1.
|
I. |
|
reciprocals |
|
II. |
|
not reciprocals |
|
III. |
|
reciprocals |
The correct answer is D.
19. A rope 20.6 meters long is cut into two pieces. If the length of one piece of rope is 2.8 meters shorter than the length of the other, what is the length, in meters, of the longer piece of rope?
1. (A) 7.5
2. (B) 8.9
3. (C) 9.9
4. (D) 10.3
5. (E) 11.7
Algebra First-order equations
If x represents the length of the longer piece of rope, then x − 2.8 represents the length of the shorter piece, where both lengths are in meters. The total length of the two pieces of rope is 20.6 meters so,
|
x + (x − 2.8) = 20.6 |
given |
|
2x − 2.8 = 20.6 |
add like terms |
|
2x = 23.4 |
add 2.8 to both sides |
|
x = 11.7 |
divide both sides by 2 |
Thus, the length of the longer piece of rope is 11.7 meters.
The correct answer is E.
20. What is the perimeter, in meters, of a rectangular garden 6 meters wide that has the same area as a rectangular playground 16 meters long and 12 meters wide?
1. (A) 48
2. (B) 56
3. (C) 60
4. (D) 76
5. (E) 192
Geometry Perimeter and area
Let L represent the length, in meters, of the rectangular garden. It is given that the width of the garden is 6 meters and the area of the garden is the same as the area of a rectangular playground that is 16 meters long and 12 meters wide. It follows that 6L = (16)(12), and so L = 32. The perimeter of the garden is, then, 2(32 + 6) = 2(38) = 76 meters.
The correct answer is D.
21. Of the total amount that Jill spent on a shopping trip, excluding taxes, she spent 50 percent on clothing, 20 percent on food, and 30 percent on other items. If Jill paid a 4 percent tax on the clothing, no tax on the food, and an 8 percent tax on all other items, then the total tax that she paid was what percent of the total amount that she spent, excluding taxes?
1. (A) 2.8%
2. (B) 3.6%
3. (C) 4.4%
4. (D) 5.2%
5. (E) 6.0%
Arithmetic Applied problems
Let T represent the total amount Jill spent, excluding taxes. Jill paid a 4% tax on the clothing she bought, which accounted for 50% of the total amount she spent, and so the tax she paid on the clothing was (0.04)(0.5T). Jill paid an 8% tax on the other items she bought, which accounted for 30% of the total amount she spent, and so the tax she paid on the other items was (0.08)(0.3T). Therefore, the total amount of tax Jill paid was (0.04)(0.5T) + (0.08)(0.3T) = 0.02T + 0.024T = 0.044T. The tax as a percent of the total amount Jill spent, excluding taxes, was 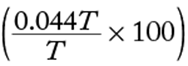 % = 4.4%.
% = 4.4%.
The correct answer is C.
22. At the opening of a trading day at a certain stock exchange, the price per share of stock K was $8. If the price per share of stock K was $9 at the closing of the day, what was the percent increase in the price per share of stock K for that day?
1. (A) 1.4%
2. (B) 5.9%
3. (C) 11.1%
4. (D) 12.5%
5. (E) 23.6%
Arithmetic Percents
An increase from $8 to $9 represents an increase of 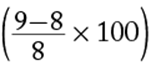 % =
% = ![]() % = 12.5%.
% = 12.5%.
The correct answer is D.
23. The price of a certain television set is discounted by 10 percent, and the reduced price is then discounted by 10 percent. This series of successive discounts is equivalent to a single discount of
1. (A) 20%
2. (B) 19%
3. (C) 18%
4. (D) 11%
5. (E) 10%
Arithmetic Percents
If P represents the original price of the television, then after a discount of 10 percent, the reduced price is ![]() . When the reduced price is discounted by 10 percent, the resulting price is
. When the reduced price is discounted by 10 percent, the resulting price is ![]()
![]()
![]() . This price is the original price of the television discounted by 19 percent.
. This price is the original price of the television discounted by 19 percent.
The correct answer is B.
24. The number of rooms at Hotel G is 10 less than twice the number of rooms at Hotel H. If the total number of rooms at Hotel G and Hotel H is 425, what is the number of rooms at Hotel G?
1. (A) 140
2. (B) 180
3. (C) 200
4. (D) 240
5. (E) 280
Algebra Simultaneous equations
Let G be the number of rooms in Hotel G and let H be the number of rooms in Hotel H. Expressed in symbols, the given information is the following system of equations
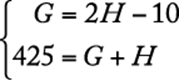
Solving the second equation for H gives ![]() . Then, substituting
. Then, substituting ![]() for H in the first equation gives
for H in the first equation gives
![]()
![]()
![]()
![]()
![]()
The correct answer is E.
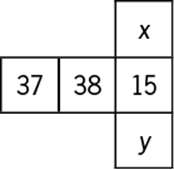
25. In the figure above, the sum of the three numbers in the horizontal row equals the product of the three numbers in the vertical column. What is the value of xy?
1. (A) 6
2. (B) 15
3. (C) 35
4. (D) 75
5. (E) 90
Arithmetic Operations on rational numbers
The sum of the three numbers in the horizontal row is ![]() , or 90. The product of the three numbers in the vertical column is 15xy. Thus,
, or 90. The product of the three numbers in the vertical column is 15xy. Thus, ![]() , or the value of
, or the value of ![]() .
.
The correct answer is A.
26. ![]()
1. (A) −4
2. (B) 2
3. (C) 6
4. (D) ![]()
5. (E) ![]()
Arithmetic Operations on radical expressions
Work the problem.
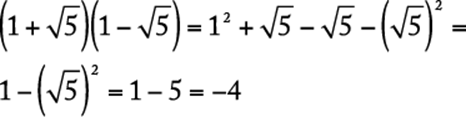
The correct answer is A.
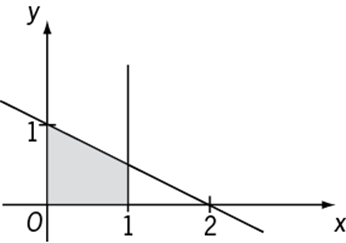
27. In the rectangular coordinate system above, the shaded region is bounded by straight lines. Which of the following is NOT an equation of one of the boundary lines?
1. (A) ![]()
2. (B) ![]()
3. (C) ![]()
4. (D) ![]()
5. (E) ![]()
Geometry Simple coordinate geometry
The left boundary of the shaded region is the y-axis, which has equation ![]() . The bottom boundary of the shaded region is the x-axis, which has equation
. The bottom boundary of the shaded region is the x-axis, which has equation ![]() . The right boundary of the shaded region is the vertical line that has equation
. The right boundary of the shaded region is the vertical line that has equation ![]() since it goes through (1,0). The top boundary of the shaded region is the line that goes through (0,1) and (2,0). The equation of this line CANNOT be
since it goes through (1,0). The top boundary of the shaded region is the line that goes through (0,1) and (2,0). The equation of this line CANNOT be ![]() because
because ![]() and also
and also ![]() . The equation of this line is
. The equation of this line is ![]() since both (0,1) and (2,0) are on this line (i.e.,
since both (0,1) and (2,0) are on this line (i.e., ![]() ).
).
The correct answer is D.
28. A certain population of bacteria doubles every 10 minutes. If the number of bacteria in the population initially was 104, what was the number in the population 1 hour later?
1. (A) 2(104)
2. (B) 6(104)
3. (C) (26)(104)
4. (D) (106)(104)
5. (E) (104)6
Arithmetic Operations on rational numbers
If the population of bacteria doubles every 10 minutes, it doubles 6 times in one hour. This doubling action can be expressed as (2)(2)(2)(2)(2)(2) or 26. Thus, if the initial population is 104, the population will be (26)(104) after one hour.
The correct answer is C.
29. If the perimeter of a rectangular garden plot is 34 feet and its area is 60 square feet, what is the length of each of the longer sides?
1. (A) 5 ft
2. (B) 6 ft
3. (C) 10 ft
4. (D) 12 ft
5. (E) 15 ft
Geometry; Algebra Perimeter; Area; Simultaneous equations
Letting x represent the length of the rectangular garden and y represent the width of the garden in the formulas for calculating perimeter and area, the given information can be expressed as:
|
|
|
|
or |
|
|
|
|
|
|
|
This reduces the problem to finding two numbers whose sum is 17 and whose product is 60. It can be seen by inspection that the two numbers are 5 and 12, so the length of each of the longer sides of the garden is 12 ft.
It is also possible to solve ![]() for y and substitute the value of
for y and substitute the value of ![]() in the equation for the area and solve for x:
in the equation for the area and solve for x:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Thus, the length of each of the longer sides of the garden must be 12 ft.
The correct answer is D.
30. In a poll of 66,000 physicians, only 20 percent responded; of these, 10 percent disclosed their preference for pain reliever X. How many of the physicians who responded did not disclose a preference for pain reliever X?
1. (A) 1,320
2. (B) 5,280
3. (C) 6,600
4. (D) 10,560
5. (E) 11,880
Arithmetic Percents
The number of physicians who responded to the poll was ![]() . If 10 percent of the respondents disclosed a preference for X, then 90 percent did not disclose a preference for X. Thus, the number of respondents who did not disclose a preference is
. If 10 percent of the respondents disclosed a preference for X, then 90 percent did not disclose a preference for X. Thus, the number of respondents who did not disclose a preference is ![]() .
.
The correct answer is E.
31. 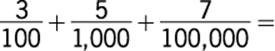
1. (A) 0.357
2. (B) 0.3507
3. (C) 0.35007
4. (D) 0.0357
5. (E) 0.03507
Arithmetic Operations on rational numbers
If each fraction is written in decimal form, the sum to be found is
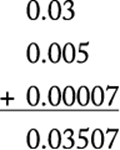
The correct answer is E.
32. Which of the following fractions is equal to the decimal 0.0625?
1. (A) ![]()
2. (B) ![]()
3. (C) ![]()
4. (D) ![]()
5. (E) ![]()
Arithmetic Operations on rational numbers
Work the problem.
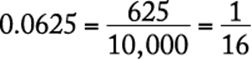
The correct answer is C.
33. If r and s are positive integers such that (2r)(4s) = 16, then 2r + s =
1. (A) 2
2. (B) 3
3. (C) 4
4. (D) 5
5. (E) 6
Algebra Exponents
Using the rules of exponents,
|
(2r)(4s) = 16 |
given |
|
(2r)(22s) = 24 |
4s = (22)s = 22s, 16 = 24 |
|
2r+ 2s = 24 |
addition property of exponents |
Thus, r + 2s = 4. However, the problem asks for the value of 2r + s. Since r and s are positive integers, s < 2; otherwise, r would not be positive.
Therefore, s = 1, and it follows that r + (2)(1) = 4, or r = 2. The value of 2r + s is (2)(2) + 1 = 5.
Alternatively, since (2r)(4s) = 16 and both r and s are positive, it follows that s < 2; otherwise, 4s ≥ 16 and r would not be positive. Therefore, s = 1 and (2r)(4) = 16. It follows that 2r = 4 and r = 2. The value of 2r + s is (2)(2) + 1 = 5.
The correct answer is D.
34. If positive integers x and y are not both odd, which of the following must be even?
1. (A) xy
2. (B) ![]()
3. (C) ![]()
4. (D) ![]()
5. (E) ![]()
Arithmetic Properties of numbers
Since it is given that x and y are NOT both odd, either both x and y are even or one is even and the other one is odd. The following table clearly shows that only the product of x and y must be even.
|
Both x and y even |
One of x or y even, the other odd |
|
|
xy |
Even |
Even |
|
|
Even |
Odd |
|
|
Even |
Odd |
|
|
Odd |
Even |
|
|
Odd |
Odd |
The correct answer is A.
35. The annual budget of a certain college is to be shown on a circle graph. If the size of each sector of the graph is to be proportional to the amount of the budget it represents, how many degrees of the circle should be used to represent an item that is 15 percent of the budget?
1. (A) ![]()
2. (B) ![]()
3. (C) ![]()
4. (D) ![]()
5. (E) ![]()
Arithmetic Percents; Interpretation of graphs
Since there are 360 degrees in a circle, the measure of the central angle in the circle should be ![]() .
.
The correct answer is C.
36. During a two-week period, the price of an ounce of silver increased by 25 percent by the end of the first week and then decreased by 20 percent of this new price by the end of the second week. If the price of silver was x dollars per ounce at the beginning of the two-week period, what was the price, in dollars per ounce, by the end of the period?
1. (A) 0.8x
2. (B) 0.95x
3. (C) x
4. (D) 1.05x
5. (E) 1.25x
Arithmetic Percents
At the end of the first week the price of an ounce of silver was 1.25x. At the end of the second week, the price was 20 percent less than this, or 80 percent of 1.25x, which is (0.80)(1.25)x, which is in turn equal to x.
The correct answer is C.
37. In a certain pond, 50 fish were caught, tagged, and returned to the pond. A few days later, 50 fish were caught again, of which 2 were found to have been tagged. If the percent of tagged fish in the second catch approximates the percent of tagged fish in the pond, what is the approximate number of fish in the pond?
1. (A) 400
2. (B) 625
3. (C) 1,250
4. (D) 2,500
5. (E) 10,000
Algebra Applied problems
To solve this problem, it is necessary to determine two fractions: the fraction of fish tagged and the fraction of fish then caught that were already tagged. These two fractions can then be set equal in a proportion, and the problem can be solved.
Letting N be the approximate total number of fish in the pond, then ![]() is the fraction of fish in the pond that were tagged in the first catch. Then, the fraction of tagged fish in the sample of 50 that were caught in the second catch can be expressed as
is the fraction of fish in the pond that were tagged in the first catch. Then, the fraction of tagged fish in the sample of 50 that were caught in the second catch can be expressed as ![]() , or
, or ![]() . Therefore,
. Therefore, 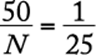 , or
, or ![]() .
.
The correct answer is C.
38. ![]()
1. (A) ![]()
2. (B) ![]()
3. (C) ![]()
4. (D) 8
5. (E) 16
Arithmetic Operations on radical expressions
Working this problem gives
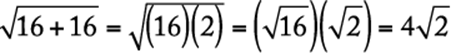
The correct answer is A.
39. The organizers of a fair projected a 25 percent increase in attendance this year over that of last year, but attendance this year actually decreased by 20 percent. What percent of the projected attendance was the actual attendance?
1. (A) 45%
2. (B) 56%
3. (C) 64%
4. (D) 75%
5. (E) 80%
Arithmetic Percents
Letting A be last year”s attendance, set up the given information, and work the problem.
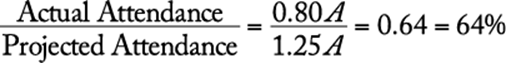
The correct answer is C.
40. What is the ratio of ![]() to the product
to the product ![]() ?
?
1. (A) ![]()
2. (B) ![]()
3. (C) ![]()
4. (D) ![]()
5. (E) 4
Arithmetic Operations on rational numbers
Work the problem.
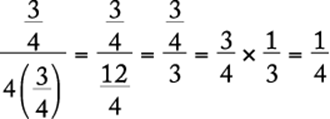
The correct answer is A.
41. If ![]() , then
, then ![]()
1. (A) −24
2. (B) −8
3. (C) 0
4. (D) 8
5. (E) 24
Algebra First-degree equations
Work the problem.
|
|
|
|
|
add 3 to both sides; add x to both sides |
|
|
divide both sides by 3 |
Therefore, ![]() .
.
The correct answer is D.
![]()
![]()
42. In the system of equations above, what is the value of x?
1. (A) −3
2. (B) −1
3. (C) ![]()
4. (D) 1
5. (E) ![]()
Algebra Simultaneous equations
Solving the second equation for y gives ![]() . Then, substituting
. Then, substituting ![]() for y in the first equation gives
for y in the first equation gives
![]()
![]()
![]()
![]()
![]()
The correct answer is D.
43. If ![]() , then the value of
, then the value of ![]() is closest to
is closest to
1. (A) ![]()
2. (B) ![]()
3. (C) ![]()
4. (D) ![]()
5. (E) ![]()
Algebra Simplifying algebraic expressions
For all large values of x, the value of ![]() is going to be very close to the value of
is going to be very close to the value of ![]() , which is equal to
, which is equal to ![]() .
.
The correct answer is D.
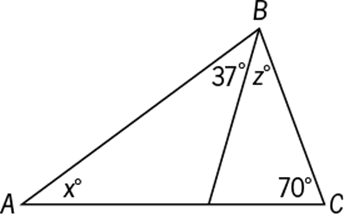
44. In ![]() above, what is x in terms of z?
above, what is x in terms of z?
1. (A) ![]()
2. (B) ![]()
3. (C) ![]()
4. (D) ![]()
5. (E) ![]()
Geometry Angle measure in degrees
Since the sum of the degree measures of the angles in a triangle equals ![]() ,
, ![]() . Solve this equation for x.
. Solve this equation for x.
![]()
![]()
![]()
![]()
The correct answer is E.
45. What is the maximum number of ![]() foot pieces of wire that can be cut from a wire that is 24 feet long?
foot pieces of wire that can be cut from a wire that is 24 feet long?
1. (A) 11
2. (B) 18
3. (C) 19
4. (D) 20
5. (E) 30
Arithmetic Operations on rational numbers
In working the problem, 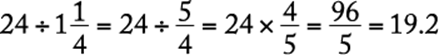 . Since full
. Since full ![]() foot pieces of wire are needed, 19 pieces can be cut.
foot pieces of wire are needed, 19 pieces can be cut.
The correct answer is C.
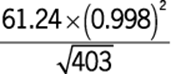
46. The expression above is approximately equal to
1. (A) 1
2. (B) 3
3. (C) 4
4. (D) 5
5. (E) 6
Arithmetic Operations on radical expressions
Simplify the expression using approximations.
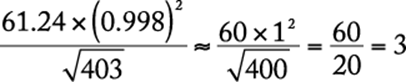
The correct answer is B.
47. If the numbers ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() were ordered from greatest to least, the middle number of the resulting sequence would be
were ordered from greatest to least, the middle number of the resulting sequence would be
1. (A) ![]()
2. (B) ![]()
3. (C) ![]()
4. (D) ![]()
5. (E) ![]()
Arithmetic Operations on rational numbers
The least common denominator for all the fractions in the problem is 48. Work out their equivalencies to see clearly their relative values: 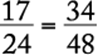 ,
, 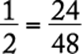 ,
, 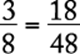 ,
, 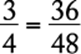 ,
, 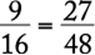 In descending order, they are
In descending order, they are ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and the middle number is
, and the middle number is 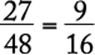 .
.
The correct answer is E.
48. Last week Jack worked 70 hours and earned $1,260. If he earned his regular hourly wage for the first 40 hours worked, 1![]() times his regular hourly wage for the next 20 hours worked, and 2 times his regular hourly wage for the remaining 10 hours worked, what was his regular hourly wage?
times his regular hourly wage for the next 20 hours worked, and 2 times his regular hourly wage for the remaining 10 hours worked, what was his regular hourly wage?
1. A. $7.00
2. B. $14.00
3. C. $18.00
4. D. $22.00
5. E. $31.50
Algebra First-degree equations
If w represents Jack”s regular hourly wage, then Jack”s earnings for the week can be represented by the sum of the following amounts, in dollars: 40w (his earnings for the first 40 hours he worked), (20)(1.5w) (his earnings for the next 20 hours he worked), and (10)(2w) (his earnings for the last 10 hours he worked). Therefore,
|
40w + (20)(1.5w) + (10)(2w) = 1,260 |
given |
|
90w = 1,260 |
add like terms |
|
w = 14 |
divide both sides by 90 |
Jack”s regular hourly wage was $14.00.
The correct answer is B.
49. Last year if 97 percent of the revenues of a company came from domestic sources and the remaining revenues, totaling $450,000, came from foreign sources, what was the total of the company”s revenues?
1. (A) $1,350,000
2. (B) $1,500,000
3. (C) $4,500,000
4. (D) $15,000,000
5. (E) $150,000,000
Arithmetic Percents
If 97 percent of the revenues came from domestic sources, then the remaining 3 percent, totaling $450,000, came from foreign sources. Letting x represent the total revenue, this information can be expressed as ![]() , and thus
, and thus 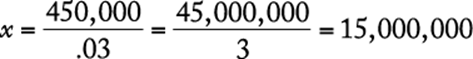 .
.
The correct answer is D.
50. 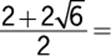
1. (A) ![]()
2. (B) ![]()
3. (C) ![]()
4. (D) ![]()
5. (E) ![]()
Arithmetic Operations on radical expressions
Rewrite the expression to eliminate the denominator.
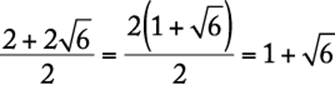
or
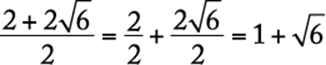
The correct answer is C.
51. A certain fishing boat is chartered by 6 people who are to contribute equally to the total charter cost of $480. If each person contributes equally to a $150 down payment, how much of the charter cost will each person still owe?
1. (A) $80
2. (B) $66
3. (C) $55
4. (D) $50
5. (E) $45
Arithmetic Operations on rational numbers
Since each of the 6 individuals contributes equally to the $150 down payment, and since it is given that the total cost of the chartered boat is $480, each person still owes 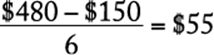 .
.
The correct answer is C.
52. Craig sells major appliances. For each appliance he sells, Craig receives a commission of $50 plus 10 percent of the selling price. During one particular week Craig sold 6 appliances for selling prices totaling $3,620. What was the total of Craig”s commissions for that week?
1. (A) $412
2. (B) $526
3. (C) $585
4. (D) $605
5. (E) $662
Arithmetic Percents
Since Craig receives a commission of $50 on each appliance plus a 10 percent commission on total sales, his commission for that week was ![]() .
.
The correct answer is E.
53. What number when multiplied by ![]() yields
yields ![]() as the result?
as the result?
1. (A) ![]()
2. (B) ![]()
3. (C) ![]()
4. (D) ![]()
5. (E) ![]()
Algebra First-degree equations
Letting n represent the number, this problem can be expressed as 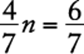 , which can be solved for n by multiplying both sides by
, which can be solved for n by multiplying both sides by ![]() :
:
|
|
|
|
|
multiply both sides by |
|
|
reduce the fraction |
The correct answer is C.
54. If 3 pounds of dried apricots that cost x dollars per pound are mixed with 2 pounds of prunes that cost y dollars per pound, what is the cost, in dollars, per pound of the mixture?
1. (A) 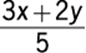
2. (B) 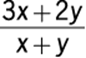
3. (C) 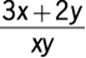
4. (D) ![]()
5. (E) ![]()
Algebra Applied problems; Simplifying algebraic expressions
The total number of pounds in the mixture is ![]() pounds, and the total cost of the mixture is
pounds, and the total cost of the mixture is ![]() dollars. Therefore, the cost per pound of the mixture is
dollars. Therefore, the cost per pound of the mixture is 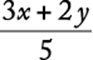 dollars.
dollars.
The correct answer is A.
55. Which of the following must be equal to zero for all real numbers x?
I. ![]()
II. ![]()
III. x0
1. (A) I only
2. (B) II only
3. (C) I and III only
4. (D) II and III only
5. (E) I, II, and III
Arithmetic Properties of numbers
Consider the numeric properties of each answer choice.
I. 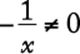 for all real numbers x.
for all real numbers x.
II. ![]() for all real numbers x
for all real numbers x
III. ![]() for all nonzero real numbers x Thus, only the expression in II must be equal to zero for all real numbers x.
for all nonzero real numbers x Thus, only the expression in II must be equal to zero for all real numbers x.
The correct answer is B.
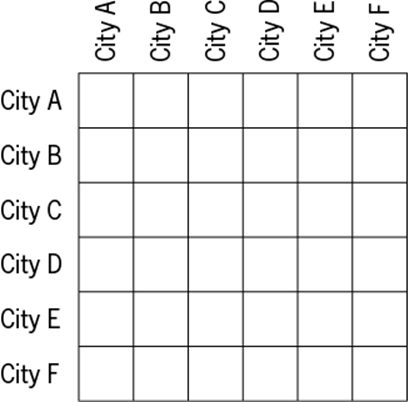
56. In the table above, what is the least number of table entries that are needed to show the mileage between each city and each of the other five cities?
1. (A) 15
2. (B) 21
3. (C) 25
4. (D) 30
5. (E) 36
Arithmetic Interpretation of tables
Since there is no mileage between a city and itself and since the mileage for each pair of cities needs to be entered only once, only those boxes below (or above) the diagonal from the upper left to the lower right need entries. This gives ![]() entries.
entries.
The correct answer is A.
57. If ![]() is a factor of
is a factor of ![]() , then
, then ![]()
1. (A) −6
2. (B) −2
3. (C) 2
4. (D) 6
5. (E) 14
Algebra Second-degree equations
If ![]() is a factor of the expression
is a factor of the expression ![]() , then
, then ![]() is a solution of the equation
is a solution of the equation ![]() . So,
. So,
![]()
![]()
![]()
![]()
![]()
The correct answer is C.
58. ![]()
1. (A) 0.248
2. (B) 0.252
3. (C) 0.284
4. (D) 0.312
5. (E) 0.320
Arithmetic Operations on rational numbers
To avoid long division, multiply the given fraction by 1 using a form for 1 that will result in a power of 10 in the denominator.
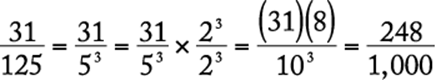
![]()
The correct answer is A.
59. Members of a social club met to address 280 newsletters. If they addressed ![]() of the newsletters during the first hour and
of the newsletters during the first hour and ![]() of the remaining newsletters during the second hour, how many newsletters did they address during the second hour?
of the remaining newsletters during the second hour, how many newsletters did they address during the second hour?
1. (A) 28
2. (B) 42
3. (C) 63
4. (D) 84
5. (E) 112
Arithmetic Operations on rational numbers
Since ![]() of the newsletters were addressed during the first hour,
of the newsletters were addressed during the first hour, 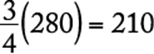 newsletters were NOT addressed during the first hour and remained to be done in the second hour. Therefore,
newsletters were NOT addressed during the first hour and remained to be done in the second hour. Therefore, 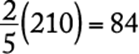 newsletters were addressed during the second hour.
newsletters were addressed during the second hour.
The correct answer is D.
60. 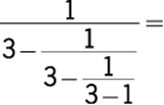
1. (A) ![]()
2. (B) ![]()
3. (C) ![]()
4. (D) ![]()
5. (E) ![]()
Arithmetic Operations with rational numbers
Perform each subtraction beginning at the lowest level in the fraction and proceeding upward.
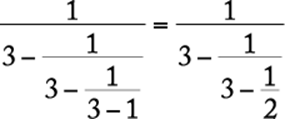
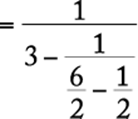
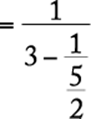
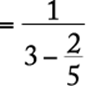
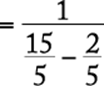
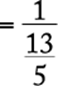
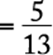
The correct answer is B.
61. After 4,000 gallons of water were added to a large water tank that was already filled to ![]() of its capacity, the tank was then at
of its capacity, the tank was then at ![]() of its capacity. How many gallons of water does the tank hold when filled to capacity?
of its capacity. How many gallons of water does the tank hold when filled to capacity?
1. (A) 5,000
2. (B) 6,200
3. (C) 20,000
4. (D) 40,000
5. (E) 80,000
Algebra First-degree equations
Let C be the capacity of the tank. In symbols, the given information is 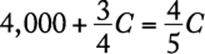 . Solve for C.
. Solve for C.
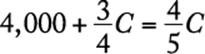
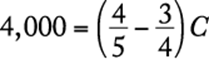
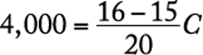
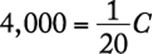
![]()
![]()
The correct answer is E.
62. The sum of three integers is 40. The largest integer is 3 times the middle integer, and the smallest integer is 23 less than the largest integer. What is the product of the three integers?
1. (A) 1,104
2. (B) 972
3. (C) 672
4. (D) 294
5. (E) 192
Algebra Simultaneous equations
Let the three integers be x, y, and z, where ![]() . Then, in symbols the given information is
. Then, in symbols the given information is
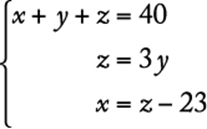
Substituting 3y for z in the third equation gives ![]() . Then, substituting
. Then, substituting ![]() for x and 3y for z into the first equation gives
for x and 3y for z into the first equation gives
![]()
![]()
![]()
![]()
From ![]() , it follows that
, it follows that ![]() and
and ![]() . Thus, the product of x, y, and z is
. Thus, the product of x, y, and z is ![]() .
.
The correct answer is B.
63. Five machines at a certain factory operate at the same constant rate. If four of these machines, operating simultaneously, take 30 hours to fill a certain production order, how many fewer hours does it take all five machines, operating simultaneously, to fill the same production order?
1. (A) 3
2. (B) 5
3. (C) 6
4. (D) 16
5. (E) 24
Arithmetic Applied problems
If 4 machines, working simultaneously, each work for 30 hours to fill a production order, it takes (4)(30) machine hours to fill the order. If 5 machines are working simultaneously, it will take ![]() hours. Thus, 5 machines working simultaneously will take 30 − 24 = 6 fewer hours to fill the production order than 4 machines working simultaneously.
hours. Thus, 5 machines working simultaneously will take 30 − 24 = 6 fewer hours to fill the production order than 4 machines working simultaneously.
The correct answer is C.
64. If Mel saved more than $10 by purchasing a sweater at a 15 percent discount, what is the smallest amount the original price of the sweater could be, to the nearest dollar?
1. (A) 45
2. (B) 67
3. (C) 75
4. (D) 83
5. (E) 150
Arithmetic; Algebra Percents; Inequalities; Applied problems
Letting P be the original price of the sweater in dollars, the given information can be expressed as ![]() . Solving for P gives
. Solving for P gives
![]()
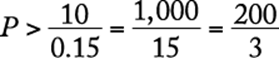
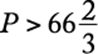
Thus, to the nearest dollar, the smallest amount P could have been is $67.
The correct answer is B.
65. If ![]() and d∗ is the decimal obtained by rounding d to the nearest hundredth, what is the value of
and d∗ is the decimal obtained by rounding d to the nearest hundredth, what is the value of ![]() ?
?
1. (A) − 0.0053
2. (B) − 0.0003
3. (C) 0.0007
4. (D) 0.0047
5. (E) 0.0153
Arithmetic Operations on rational numbers
Since ![]() rounded to the nearest hundredth is 2.05,
rounded to the nearest hundredth is 2.05, ![]() ; therefore,
; therefore, ![]() .
.
The correct answer is D.
66. At a monthly meeting, ![]() of the attendees were males and
of the attendees were males and ![]() of the male attendees arrived on time. If
of the male attendees arrived on time. If ![]() of the female attendees arrived on time, what fraction of the attendees at the monthly meeting did not arrive on time?
of the female attendees arrived on time, what fraction of the attendees at the monthly meeting did not arrive on time?
1. (A) ![]()
2. (B) ![]()
3. (C) ![]()
4. (D) ![]()
5. (E) ![]()
Arithmetic Operations with rational numbers
Let T be the total number of attendees at the meeting. Then, ![]() is the number of male attendees. Of these,
is the number of male attendees. Of these, ![]() arrived on time, so
arrived on time, so 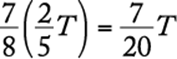 is the number of male attendees who arrived on time. Since
is the number of male attendees who arrived on time. Since ![]() of the attendees were male, the number of female attendees is
of the attendees were male, the number of female attendees is 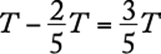 . Of these
. Of these ![]() arrived on time, so
arrived on time, so 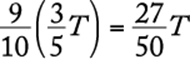 is the number of female attendees who arrived on time. The total number of attendees who arrived on time is therefore
is the number of female attendees who arrived on time. The total number of attendees who arrived on time is therefore 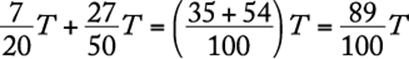 . Thus, the number of attendees who did NOT arrive on time is
. Thus, the number of attendees who did NOT arrive on time is 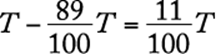 , so the fraction of attendees who did not arrive on time is
, so the fraction of attendees who did not arrive on time is ![]() .
.
The correct answer is A.
67. The sequence a1, a2, a3, a4, a5 is such that ![]() for
for ![]() . If
. If ![]() , what is the value of a1?
, what is the value of a1?
1. (A) 1
2. (B) 6
3. (C) 11
4. (D) 16
5. (E) 21
Algebra Sequences
Since ![]() , then
, then ![]() . So,
. So,
![]()
![]()
![]()
![]()
Adding the equations gives
![]()
![]()
![]()
and substituting 31 for a5 gives
![]()
![]() .
.
The correct answer is C.
68. A certain bridge is 4,024 feet long. Approximately how many minutes does it take to cross this bridge at a constant speed of 20 miles per hour? (1 mile = 5,280 feet)
1. (A) 1
2. (B) 2
3. (C) 4
4. (D) 6
5. (E) 7
Arithmetic Applied problems
First, convert 4,024 feet to miles since the speed is given in miles per hour: ![]() =
= ![]() mi. Now, divide by 20 mph:
mi. Now, divide by 20 mph: ![]() mi ÷
mi ÷ ![]() .
.
Last, convert ![]() to minutes:
to minutes: ![]() ≈
≈ ![]() min. Then,
min. Then, ![]() min = 0.8 × 3 min ≈ 2 min. Thus, at a constant speed of 20 miles per hour, it takes approximately 2 minutes to cross the bridge.
min = 0.8 × 3 min ≈ 2 min. Thus, at a constant speed of 20 miles per hour, it takes approximately 2 minutes to cross the bridge.
The correct answer is B.
69. If ![]() , how much greater than the median of the numbers in S is the mean of the numbers in S?
, how much greater than the median of the numbers in S is the mean of the numbers in S?
1. (A) 0.5
2. (B) 1.0
3. (C) 1.5
4. (D) 2.0
5. (E) 2.5
Arithmetic; Algebra Statistics; Concepts of sets
The median of S is found by ordering the values according to size (0, 2, 4, 5, 8, 11) and taking the average of the two middle numbers: 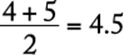 . The mean is
. The mean is 
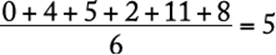 .
.
The difference between the mean and the median is ![]() .
.
The correct answer is A.
70. A total of 5 liters of gasoline is to be poured into two empty containers with capacities of 2 liters and 6 liters, respectively, such that both containers will be filled to the same percent of their respective capacities. What amount of gasoline, in liters, must be poured into the 6-liter container?
1. (A) ![]()
2. (B) 4
3. (C) ![]()
4. (D) 3
5. (E) ![]()
Algebra Ratio and proportion
If x represents the amount, in liters, of gasoline poured into the 6-liter container, then 5 − x represents the amount, in liters, of gasoline poured into the 2-liter container. After the gasoline is poured into the containers, the 6-liter container will be filled to ![]() of its capacity and the 2-liter container will be filled to
of its capacity and the 2-liter container will be filled to ![]() of its capacity. Because these two percents are equal,
of its capacity. Because these two percents are equal,
|
|
given |
|
2x = 6(5 − x) |
multiply both sides by 12 |
|
2x = 30 − 6x |
use distributive property |
|
8x = 30 |
add 6x to both sides |
|
|
divide both sides by 8 |
Therefore, ![]() liters of gasoline must be poured into the 6-liter container.
liters of gasoline must be poured into the 6-liter container.
The correct answer is C.
71. When positive integer n is divided by 5, the remainder is 1. When n is divided by 7, the remainder is 3. What is the smallest positive integer k such that ![]() is a multiple of 35?
is a multiple of 35?
1. (A) 3
2. (B) 4
3. (C) 12
4. (D) 32
5. (E) 35
Arithmetic Properties of numbers
Given that the remainder is 1 when the positive integer n is divided by 5, it follows that ![]() for some positive integer p. Likewise, the remainder is 3 when n is divided by 7, so
for some positive integer p. Likewise, the remainder is 3 when n is divided by 7, so ![]() for some positive integer q. Equating the two expressions for ngives
for some positive integer q. Equating the two expressions for ngives ![]() or
or ![]() . Since the units digit of each multiple of 5 is either 5 or 0, the units digit of
. Since the units digit of each multiple of 5 is either 5 or 0, the units digit of ![]() must be 5 or 0 and the units digit of 7q must be 3 or 8. Therefore,
must be 5 or 0 and the units digit of 7q must be 3 or 8. Therefore, ![]() , 63, 98, 133, . . . , and so
, 63, 98, 133, . . . , and so ![]() , 9, 14, 19, . . . . Thus,
, 9, 14, 19, . . . . Thus, ![]() for some positive integer m. Then,
for some positive integer m. Then, ![]()
![]()
![]() . Therefore, if k is a positive integer,
. Therefore, if k is a positive integer, ![]() is a multiple of 35 when
is a multiple of 35 when ![]() , 39, 74, . . . and the smallest of these values of k is 4.
, 39, 74, . . . and the smallest of these values of k is 4.
The correct answer is B.
72. List S consists of 10 consecutive odd integers, and list T consists of 5 consecutive even integers. If the least integer in S is 7 more than the least integer in T, how much greater is the average (arithmetic mean) of the integers in S than the average of the integers inT?
1. (A) 2
2. (B) 7
3. (C) 8
4. (D) 12
5. (E) 22
Arithmetic Statistics
Let the integers in S be s, ![]() ,
, ![]() , . . . ,
, . . . , ![]() , where s is odd. Let the integers in T be t,
, where s is odd. Let the integers in T be t, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , where t is even. Given that
, where t is even. Given that ![]() , it follows that
, it follows that ![]() . The average of the integers in S is
. The average of the integers in S is 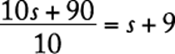 , and, similarly, the average of the integers in T is
, and, similarly, the average of the integers in T is 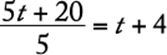 . The difference in these averages is
. The difference in these averages is ![]() . Thus, the average of the integers in S is 12 greater than the average of the integers in T.
. Thus, the average of the integers in S is 12 greater than the average of the integers in T.
The correct answer is D.
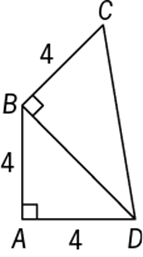
73. In the figure above, what is the area of triangular region BCD?
1. (A) ![]()
2. (B) 8
3. (C) ![]()
4. (D) 16
5. (E) ![]()
Geometry Triangles; Area
By the Pythagorean theorem, ![]() . Then the area of
. Then the area of ![]() is
is 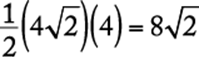 .
.
The correct answer is C.
74. Of the goose eggs laid at a certain pond, ![]() hatched, and
hatched, and ![]() of the geese that hatched from those eggs survived the first month. Of the geese that survived the first month,
of the geese that hatched from those eggs survived the first month. Of the geese that survived the first month, ![]() did not survive the first year. If 120 geese survived the first year and if no more than one goose hatched from each egg, how many goose eggs were laid at the pond?
did not survive the first year. If 120 geese survived the first year and if no more than one goose hatched from each egg, how many goose eggs were laid at the pond?
1. (A) 280
2. (B) 400
3. (C) 540
4. (D) 600
5. (E) 840
Arithmetic Operations with rational numbers
Let N represent the number of eggs laid at the pond. Then ![]() eggs hatched and
eggs hatched and 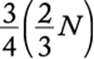 goslings (baby geese) survived the first month. Since
goslings (baby geese) survived the first month. Since ![]() of these goslings did not survive the first year, then
of these goslings did not survive the first year, then ![]() did survive the first year. This means that
did survive the first year. This means that 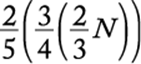 goslings survived the first year. But this number is 120 and so,
goslings survived the first year. But this number is 120 and so, 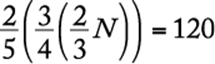 ,
, 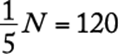 , and
, and ![]() .
.
The correct answer is D.
75. If ![]() and
and ![]() , which of the following must be equal to 0?
, which of the following must be equal to 0?
I. ![]()
II. ![]()
III. ![]()
1. (A) I only
2. (B) II only
3. (C) III only
4. (D) II and III only
5. (E) I, II, and III
Algebra Second-degree equations
Since ![]() , then
, then ![]() , so
, so ![]() or
or ![]() . Since
. Since ![]() , then
, then ![]() .
.
I. ![]()
II. ![]()
III. ![]()
The correct answer is D.
76. If a square region has area n, what is the length of the diagonal of the square in terms of n?
1. (A) ![]()
2. (B) ![]()
3. (C) ![]()
4. (D) 2n
5. (E) 2n2
Geometry Area; Pythagorean theorem
If s represents the side length of the square, then ![]() . By the Pythagorean theorem, the length of the diagonal of the square is
. By the Pythagorean theorem, the length of the diagonal of the square is ![]() .
.
The correct answer is A.
77. The “prime sum” of an integer n greater than 1 is the sum of all the prime factors of n, including repetitions. For example, the prime sum of 12 is 7, since ![]() and
and ![]() . For which of the following integers is the prime sum greater than 35?
. For which of the following integers is the prime sum greater than 35?
1. (A) 440
2. (B) 512
3. (C) 620
4. (D) 700
5. (E) 750
Arithmetic Properties of numbers
6. A Since ![]() , the prime sum of 440 is
, the prime sum of 440 is ![]() , which is not greater than 35.
, which is not greater than 35.
7. B Since ![]() , the prime sum of 512 is
, the prime sum of 512 is ![]() , which is not greater than 35.
, which is not greater than 35.
8. C Since ![]() , the prime sum of 620 is
, the prime sum of 620 is ![]() , which is greater than 35.
, which is greater than 35.
Because there can be only one correct answer, D and E need not be checked. However, for completeness,
9. D Since ![]() , the prime sum of 700 is
, the prime sum of 700 is ![]() , which is not greater than 35.
, which is not greater than 35.
10.E Since ![]() , the prime sum of 750 is
, the prime sum of 750 is ![]() , which is not greater than 35.
, which is not greater than 35.
The correct answer is C.
78. At a garage sale, all of the prices of the items sold were different. If the price of a radio sold at the garage sale was both the 15th highest price and the 20th lowest price among the prices of the items sold, how many items were sold at the garage sale?
1. (A) 33
2. (B) 34
3. (C) 35
4. (D) 36
5. (E) 37
Arithmetic Operations with integers
If the price of the radio was the 15th highest price, there were 14 items that sold for prices higher than the price of the radio. If the price of the radio was the 20th lowest price, there were 19 items that sold for prices lower than the price of the radio. Therefore, the total number of items sold is ![]() .
.
The correct answer is B.
79. For all positive integers m and v, the expression m Θ v represents the remainder when m is divided by v. What is the value of ((98 Θ 33) Θ 17) − (98 Θ (33 Θ 17))?
1. (A) −10
2. (B) −2
3. (C) 8
4. (D) 13
5. (E) 17
Arithmetic Operations with integers
First, for ((98 Θ 33) Θ 17), determine 98 Θ 33, which equals 32, since 32 is the remainder when 98 is divided by 33 (98 = 2(33) + 32). Then, determine 32 Θ 17, which equals 15, since 15 is the remainder when 32 is divided by 17 (32 = 1(17) + 15). Thus, ((98 Θ 33) Θ 17) = 15.
Next, for (98 Θ (33 Θ 17)), determine 33 Θ 17, which equals 16, since 16 is the remainder when 33 is divided by 17 (33 = 1(17) + 16). Then, determine 98 Θ 16, which equals 2, since 2 is the remainder when 98 is divided by 16 (98 = 6(16) + 2). Thus, (98 Θ (33 Θ 17)) = 2.
Finally, ((98 Θ 33) Θ 17) − (98 Θ (33 Θ 17)) = 15 − 2 = 13.
The correct answer is D.
80. In a certain sequence, each term after the first term is one-half the previous term. If the tenth term of the sequence is between 0.0001 and 0.001, then the twelfth term of the sequence is between
1. (A) 0.0025 and 0.025
2. (B) 0.00025 and 0.0025
3. (C) 0.000025 and 0.00025
4. (D) 0.0000025 and 0.000025
5. (E) 0.00000025 and 0.0000025
Arithmetic Sequences
Let an represent the nth term of the sequence. It is given that each term after the first term is ![]() the previous term and that 0.0001 < a10 < 0.001. Then, for a11,
the previous term and that 0.0001 < a10 < 0.001. Then, for a11, ![]() < a11 <
< a11 <![]() , or 0.00005 < a11 < 0.0005. For a12,
, or 0.00005 < a11 < 0.0005. For a12, ![]() < a12 <
< a12 < ![]() , or 0.000025 < a12 < 0.00025. Thus, the twelfth term of the sequence is between 0.000025 and 0.00025.
, or 0.000025 < a12 < 0.00025. Thus, the twelfth term of the sequence is between 0.000025 and 0.00025.
The correct answer is C.
81. Ada and Paul received their scores on three tests. On the first test, Ada”s score was 10 points higher than Paul”s score. On the second test, Ada”s score was 4 points higher than Paul”s score. If Paul”s average (arithmetic mean) score on the three tests was 3 points higher than Ada”s average score on the three tests, then Paul”s score on the third test was how many points higher than Ada”s score?
1. (A) 9
2. (B) 14
3. (C) 17
4. (D) 23
5. (E) 25
Algebra Statistics
Let a1, a2, and a3 be Ada”s scores on the first, second, and third tests, respectively, and let p1, p2, and p3 be Paul”s scores on the first, second, and third tests, respectively. Then, Ada”s average score is 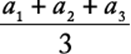 and Paul”s average score is
and Paul”s average score is 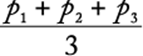 . But, Paul”s average score is 3 points higher than Ada”s average score, so
. But, Paul”s average score is 3 points higher than Ada”s average score, so 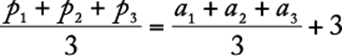 . Also, it is given that
. Also, it is given that ![]() and
and ![]() , so by substitution,
, so by substitution, 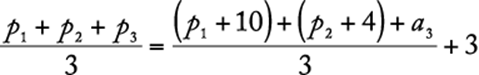 . Then,
. Then, ![]() and so
and so ![]() . On the third test, Paul”s score was 23 points higher than Ada”s score.
. On the third test, Paul”s score was 23 points higher than Ada”s score.
The correct answer is D.
82. The price of a certain stock increased by 0.25 of 1 percent on a certain day. By what fraction did the price of the stock increase that day?
1. (A) 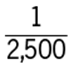
2. (B) 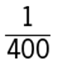
3. (C) ![]()
4. (D) ![]()
5. (E) ![]()
Arithmetic Percents
It is given that the price of a certain stock increased by 0.25 of 1 percent on a certain day. This is equivalent to an increase of ![]() of
of ![]() , which is
, which is ![]() , and
, and ![]() .
.
The correct answer is B.
83. Three business partners, Q, R, and S, agree to divide their total profit for a certain year in the ratios 2:5:8, respectively. If Q”s share was $4,000, what was the total profit of the business partners for the year?
1. (A) $26,000
2. (B) $30,000
3. (C) $52,000
4. (D) $60,000
5. (E) $300,000
Algebra Applied problems
Letting T represent the total profit and using the given ratios, Q”s share is 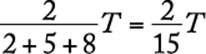 . Since Q”s share is $4,000, then
. Since Q”s share is $4,000, then 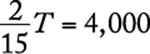 and
and 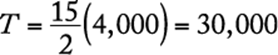 .
.
The correct answer is B.
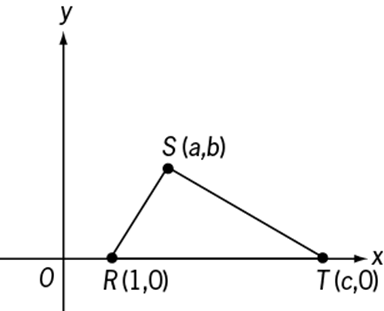
84. In the rectangular coordinate system above, the area of ![]() is
is
1. (A) ![]()
2. (B) 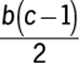
3. (C) 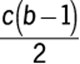
4. (D) 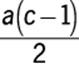
5. (E) 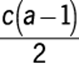
Geometry Simple-coordinate geometry
Letting ![]() be the base of the triangle, since
be the base of the triangle, since ![]() , the length of the base of
, the length of the base of ![]() is
is ![]() . The altitude to the base
. The altitude to the base ![]() is a perpendicular dropped from S to the x-axis. The length of this perpendicular is
is a perpendicular dropped from S to the x-axis. The length of this perpendicular is ![]() . Using the formula for the area, A, of a triangle,
. Using the formula for the area, A, of a triangle, 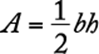 , where b is the length of the base and h is the length of the altitude to that base, the area of
, where b is the length of the base and h is the length of the altitude to that base, the area of ![]() is
is 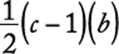 or
or 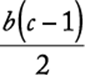 .
.
The correct answer is B.
85. What is the largest integer n such that ![]() ?
?
1. (A) 5
2. (B) 6
3. (C) 7
4. (D) 10
5. (E) 51
Arithmetic Exponents; Operations with rational numbers
Since 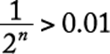 is equivalent to
is equivalent to ![]() , find the largest integer n such that
, find the largest integer n such that ![]() . Using trial and error,
. Using trial and error, ![]() and
and ![]() , but
, but ![]() and
and ![]() . Therefore, 6 is the largest integer such that
. Therefore, 6 is the largest integer such that 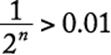 .
.
The correct answer is B.
86. The average (arithmetic mean) length per film for a group of 21 films is t minutes. If a film that runs for 66 minutes is removed from the group and replaced by one that runs for 52 minutes, what is the average length per film, in minutes, for the new group of films, in terms of t?
1. (A) ![]()
2. (B) ![]()
3. (C) 21t + 14
4. (D) ![]()
5. (E) ![]()
Arithmetic Statistics
Let S denote the sum of the lengths, in minutes, of the 21 films in the original group. Since the average length is t minutes, it follows that ![]() . If a 66-minute film is replaced by a 52-minute film, then the sum of the lengths of the 21 films in the resulting group isS − 66 + 52 = S − 14. Therefore, the average length of the resulting 21 films is
. If a 66-minute film is replaced by a 52-minute film, then the sum of the lengths of the 21 films in the resulting group isS − 66 + 52 = S − 14. Therefore, the average length of the resulting 21 films is ![]() .
.
The correct answer is B.
87. If x = −|w|, which of the following must be true?
1. A. x = −w
2. B. x = w
3. C. x2 = w
4. D. x2 = w2
5. E. x3 = w3
Algebra Absolute value
Squaring both sides of x = −|w| gives x2 = (−|w|)2, or x2 = |w|2 = w2.
Alternatively, if (x, w) is equal to either of the pairs (−1,1) or (−1,−1), then x = −|w| is true. However, each of the answer choices except x2 = w2 is false for at least one of these two pairs.
The correct answer is D.
88. Which of the following lines in the xy-plane does not contain any point with integers as both coordinates?
1. (A) ![]()
2. (B) ![]()
3. (C) ![]()
4. (D) ![]()
5. (E) ![]()
Algebra; Arithmetic Substitution; Operations with rational numbers
6. A If x is an integer, y is an integer since ![]() . Thus, the line given by
. Thus, the line given by ![]() contains points with integers as both coordinates.
contains points with integers as both coordinates.
7. B If x is an integer, then if y were an integer, then ![]() would be an integer. But,
would be an integer. But, 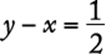 and
and ![]() is NOT an integer. Since assuming that y is an integer leads to a contradiction, then y cannot be an integer and the line given by
is NOT an integer. Since assuming that y is an integer leads to a contradiction, then y cannot be an integer and the line given by 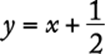 does NOT contain any points with integers as both coordinates.
does NOT contain any points with integers as both coordinates.
Since there can be only one correct answer, the lines in C, D, and E need not be checked, but for completeness,
8. C If x is an integer, ![]() is an integer and so y is an integer since
is an integer and so y is an integer since ![]() . Thus, the line given by
. Thus, the line given by ![]() contains points with integers as both coordinates.
contains points with integers as both coordinates.
9. D If x is an even integer, ![]() is an integer and so y is an integer since
is an integer and so y is an integer since 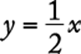 . Thus, the line given by
. Thus, the line given by 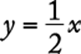 contains points with integers as both coordinates.
contains points with integers as both coordinates.
10.E If x is an even integer, ![]() is an integer and
is an integer and 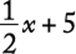 is also an integer so y is an integer since
is also an integer so y is an integer since 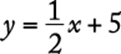 . Thus, the line given by
. Thus, the line given by 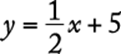 contains points with integers as both coordinates.
contains points with integers as both coordinates.
The correct answer is B.
89. One inlet pipe fills an empty tank in 5 hours. A second inlet pipe fills the same tank in 3 hours. If both pipes are used together, how long will it take to fill ![]() of the tank?
of the tank?
1. (A) ![]() hr
hr
2. (B) ![]() hr
hr
3. (C) ![]() hr
hr
4. (D) ![]() hr
hr
5. (E) ![]() hr
hr
Algebra Applied problems
If the first pipe fills the tank in 5 hours, then it fills ![]() of the tank in one hour. If the second pipe fills the tank in 3 hours, then it fills
of the tank in one hour. If the second pipe fills the tank in 3 hours, then it fills ![]() of the tank in one hour. Together, the two pipes fill
of the tank in one hour. Together, the two pipes fill 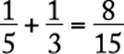 of the tank in one hour, which means they fill the whole tank in
of the tank in one hour, which means they fill the whole tank in ![]() hours. To fill
hours. To fill ![]() of the tank at this constant rate would then take
of the tank at this constant rate would then take 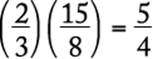 hours.
hours.
The correct answer is C.
90. 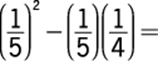
1. (A) ![]()
2. (B) ![]()
3. (C) ![]()
4. (D) ![]()
5. (E) ![]()
Arithmetic Operations on rational numbers
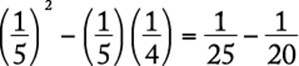
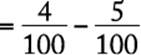
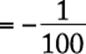
The correct answer is B.
91. If the length and width of a rectangular garden plot were each increased by 20 percent, what would be the percent increase in the area of the plot?
1. (A) 20%
2. (B) 24%
3. (C) 36%
4. (D) 40%
5. (E) 44%
Geometry Area
If L represents the length of the original plot and W represents the width of the original plot, the area of the original plot is LW. To get the dimensions of the plot after the increase, multiply each dimension of the original plot by ![]() to reflect the 20 percent increase.
to reflect the 20 percent increase.
Then, the area of the plot after the increase is ![]() or 144 percent of the area of the original plot, which is an increase of 44 percent over the area of the original plot.
or 144 percent of the area of the original plot, which is an increase of 44 percent over the area of the original plot.
The correct answer is E.
92. The population of a bacteria culture doubles every 2 minutes. Approximately how many minutes will it take for the population to grow from 1,000 to 500,000 bacteria?
1. (A) 10
2. (B) 12
3. (C) 14
4. (D) 16
5. (E) 18
Arithmetic Estimation
Set up a table of values to see how the culture grows.
|
Number of Minutes |
Bacteria Population |
|
0 |
1,000 |
|
2 |
2,000 |
|
4 |
4,000 |
|
6 |
8,000 |
|
8 |
16,000 |
|
10 |
32,000 |
|
12 |
64,000 |
|
14 |
128,000 |
|
16 |
256,000 |
|
18 |
512,000 |
At 18 minutes, the population of bacteria is just over 500,000.
The correct answer is E.
93. For a light that has an intensity of 60 candles at its source, the intensity in candles, S, of the light at a point d feet from the source is given by the formula 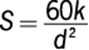 , where k is a constant. If the intensity of the light is 30 candles at a distance of 2 feet from the source, what is the intensity of the light at a distance of 20 feet from the source?
, where k is a constant. If the intensity of the light is 30 candles at a distance of 2 feet from the source, what is the intensity of the light at a distance of 20 feet from the source?
1. (A) ![]() candle
candle
2. (B) ![]() candle
candle
3. (C) 1 candle
4. (D) 2 candles
5. (E) 3 candles
Algebra Applied problems
First, solve the equation for the constant k using the values where both the intensity (S) and distance (d) are known.
|
|
|
|
|
substitute |
|
|
solve for k |
|
|
Then, with this known value of k, solve the equation for S where only the distance (d) is known.
|
|
|
|
|
substitute |
|
|
The correct answer is A.
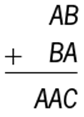
94. In the correctly worked addition problem shown, where the sum of the two-digit positive integers AB and BA is the three-digit integer AAC, and A, B, and C are different digits, what is the units digit of the integer AAC?
1. (A) 9
2. (B) 6
3. (C) 3
4. (D) 2
5. (E) 0
Arithmetic Place value
Determine the value of C.
It is given that (10A + B) + (10B + A) = 100A + 10A + C, or 11A + 11B = 110A + C. Thus, 11B − 99A = C, or 11(B − 9A) = C. Therefore, C is divisible by 11, and 0 is the only digit that is divisible by 11.
The correct answer is E.
![]()
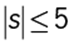
95. Given the inequalities above, which of the following CANNOT be the value of r?
1. (A) −20
2. (B) −5
3. (C) 0
4. (D) 5
5. (E) 20
Algebra Inequalities
Since |s| ≤ 5, it follows that −5 ≤ s ≤ 5. Therefore, −20 ≤ 4s ≤ 20, and hence −15 ≤ 4s + 5 ≤ 25. Since 3r ≤ 4s + 5 (given) and 4s + 5 ≤ 25 (end of previous sentence), it follows that 3r ≤ 25. Among the answer choices, 3r ≤ 25 is false only for r = 20.
The correct answer is E.
96. A positive integer is divisible by 9 if and only if the sum of its digits is divisible by 9. If n is a positive integer, for which of the following values of k is ![]() divisible by 9?
divisible by 9?
1. (A) 9
2. (B) 16
3. (C) 23
4. (D) 35
5. (E) 47
Arithmetic Properties of numbers
Since n can be any positive integer, let n = 2. Then 25 × 10n = 2,500, so its digits consist of the digits 2 and 5 followed by two digits of 0. Also, k × 102n = k × 10,000, so its digits consist of the digits of k followed by four digits of 0. Therefore, the digits of (25 × 10n) + (k × 102n) consist of the digits of k followed by the digits 2 and 5, followed by two digits of 0. The table below shows this for n = 2 and k = 35:
|
25 × 10n = |
2,500 |
|
35 × 102n = |
350,000 |
|
(25 × 10n) + (35 × 102n) = |
352,500 |
Thus, when n = 2, the sum of the digits of (25 × 10n) + (k × 102n) will be 2 + 5 = 7 plus the sum of the digits of k. Of the answer choices, this sum of digits is divisible by 9 only for k = 47, which gives 2 + 5 + 4 + 7 = 18. It can also be verified that, for each positive integer n, the only such answer choice is k = 47, although this additional verification is not necessary to obtain the correct answer.
The correct answer is E.
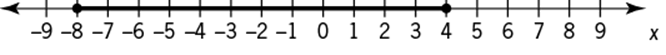
97. On the number line, the shaded interval is the graph of which of the following inequalities?
1. (A) 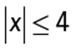
2. (B) ![]()
3. (C) ![]()
4. (D) 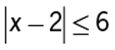
5. (E) ![]()
Algebra Inequalities; Absolute value
The midpoint of the interval from −8 to 4, inclusive, is ![]() and the length of the interval from −8 to 4, inclusive, is 4 − (−8) = 12, so the interval consists of all numbers within a distance of
and the length of the interval from −8 to 4, inclusive, is 4 − (−8) = 12, so the interval consists of all numbers within a distance of ![]() from −2. Using an inequality involving absolute values, this can be described by |x − (−2)| ≤ 6, or |x + 2| ≤ 6.
from −2. Using an inequality involving absolute values, this can be described by |x − (−2)| ≤ 6, or |x + 2| ≤ 6.
Alternatively, the inequality −8 ≤ x ≤ 4 can be written as the conjunction −8 ≤ x and x ≤ 4. Rewrite this conjunction so that the lower value, −8, and the upper value, 4, are shifted to values that have the same magnitude. This can be done by adding 2 to each side of each inequality, which gives −6 ≤ x + 2 and x + 2 ≤ 6. Thus, x + 2 lies between −6 and 6, inclusive, and it follows that |x + 2| ≤ 6.
The correct answer is E.
98. Of all the students in a certain dormitory, ![]() are first-year students and the rest are second-year students. If
are first-year students and the rest are second-year students. If ![]() of the first-year students have not declared a major and if the fraction of second-year students who have declared a major is 3 times the fraction of first-year students who have declared a major, what fraction of all the students in the dormitory are second-year students who have not declared a major?
of the first-year students have not declared a major and if the fraction of second-year students who have declared a major is 3 times the fraction of first-year students who have declared a major, what fraction of all the students in the dormitory are second-year students who have not declared a major?
1. (A) ![]()
2. (B) ![]()
3. (C) ![]()
4. (D) ![]()
5. (E) ![]()
Arithmetic Applied problems
Consider the table below in which T represents the total number of students in the dormitory. Since ![]() of the students are first-year students and the rest are second-year students, it follows that
of the students are first-year students and the rest are second-year students, it follows that ![]() of the students are second-year students, and so the totals for the first-year and second-year columns are both 0.5T. Since
of the students are second-year students, and so the totals for the first-year and second-year columns are both 0.5T. Since ![]() of the first-year students have not declared a major, it follows that the middle entry in the first-year column is
of the first-year students have not declared a major, it follows that the middle entry in the first-year column is ![]() (0.5T) = 0.4T and the first entry in the first-year column is 0.5T − 0.4T = 0.1T. Since the fraction of second-year students who have declared a major is 3 times the fraction of first-year students who have declared a major, it follows that the first entry in the second-year column is 3(0.1T) = 0.3T and the second entry in the second-year column is 0.5T − 0.3T = 0.2T. Thus, the fraction of students that are second-year students who have not declared a major is
(0.5T) = 0.4T and the first entry in the first-year column is 0.5T − 0.4T = 0.1T. Since the fraction of second-year students who have declared a major is 3 times the fraction of first-year students who have declared a major, it follows that the first entry in the second-year column is 3(0.1T) = 0.3T and the second entry in the second-year column is 0.5T − 0.3T = 0.2T. Thus, the fraction of students that are second-year students who have not declared a major is ![]() .
.
|
First-year |
Second-year |
Total |
|
|
Declared major |
0.1T |
0.3T |
0.4T |
|
Not declared major |
0.4T |
0.2T |
0.6T |
|
Total |
0.5T |
0.5T |
T |
The correct answer is B.
99. If the average (arithmetic mean) of x, y, and z is 7x and x ≠ 0, what is the ratio of x to the sum of y and z?
1. (A) 1:21
2. (B) 1:20
3. (C) 1:6
4. (D) 6:1
5. (E) 20:1
Algebra Ratio and proportion
Given that the average of x, y, and z is 7x, it follows that ![]() = 7x, or x + y + z = 21x, or y + z = 20x. Dividing both sides of the last equation by 20(y + z) gives
= 7x, or x + y + z = 21x, or y + z = 20x. Dividing both sides of the last equation by 20(y + z) gives ![]() , so the ratio of x to the sum of y and z is 1:20.
, so the ratio of x to the sum of y and z is 1:20.
The correct answer is B.
100. 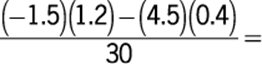
1. (A) −1.2
2. (B) −0.12
3. (C) 0
4. (D) 0.12
5. (E) 1.2
Arithmetic Operations on rational numbers
Simplify the expression.
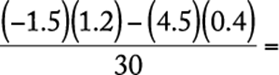
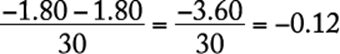
The correct answer is B.
101. René earns $8.50 per hour on days other than Sundays and twice that rate on Sundays. Last week she worked a total of 40 hours, including 8 hours on Sunday. What were her earnings for the week?
1. (A) $272
2. (B) $340
3. (C) $398
4. (D) $408
5. (E) $476
Arithmetic Operations on rational numbers
René worked a total of ![]() hours at a rate of $8.50 per hour during the week. On Sunday she worked 8 hours at a rate of
hours at a rate of $8.50 per hour during the week. On Sunday she worked 8 hours at a rate of ![]() per hour. Her total earnings for the week were thus
per hour. Her total earnings for the week were thus ![]() .
.
The correct answer is D.
102. In a shipment of 120 machine parts, 5 percent were defective. In a shipment of 80 machine parts, 10 percent were defective. For the two shipments combined, what percent of the machine parts were defective?
1. (A) 6.5%
2. (B) 7.0%
3. (C) 7.5%
4. (D) 8.0%
5. (E) 8.5%
Arithmetic Percents
The number of defective parts in the first shipment was ![]() . The number of defective parts in the second shipment was
. The number of defective parts in the second shipment was ![]() . The percent of machine parts that were defective in the two shipments combined was therefore
. The percent of machine parts that were defective in the two shipments combined was therefore 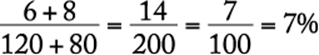 .
.
The correct answer is B.
103. If ![]() , then x =
, then x =
1. (A) − 3
2. (B) − 1
3. (C) 0
4. (D) 1
5. (E) 3
Algebra First-degree equations
To work the problem, create a common base so that the exponents can be set equal to each other.
|
|
|
|
|
since |
|
|
multiply exponents |
|
|
set exponents equal since they are on a common base (2) |
|
|
solve for x |
|
|
The correct answer is B.
104. Of the following, the closest approximation to  is
is
1. (A) 5
2. (B) 15
3. (C) 20
4. (D) 25
5. (E) 225
Arithmetic Estimation
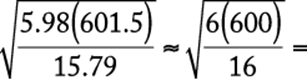
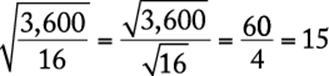
The correct answer is B.
105. Which of the following CANNOT be the greatest common divisor of two positive integers x and y?
1. (A) 1
2. (B) x
3. (C) y
4. (D) ![]()
5. (E) ![]()
Arithmetic Properties of numbers
One example is sufficient to show that a statement CAN be true.
6. A The greatest common divisor (gcd) of ![]() and
and ![]() is 1 and, therefore, 1 can be the gcd of the two positive integers x and y.
is 1 and, therefore, 1 can be the gcd of the two positive integers x and y.
7. B The greatest common divisor (gcd) of ![]() and
and ![]() is 3 and therefore x can be the gcd of the two positive integers x and y.
is 3 and therefore x can be the gcd of the two positive integers x and y.
8. C The greatest common divisor (gcd) of ![]() and
and ![]() is 3 and therefore y can be the gcd of the two positive integers x and y.
is 3 and therefore y can be the gcd of the two positive integers x and y.
9. D The greatest common divisor (gcd) of ![]() and
and ![]() is 1. Since
is 1. Since ![]() ,
, ![]() can be the gcd of the two positive integers x and y.
can be the gcd of the two positive integers x and y.
By the process of elimination, ![]() CANNOT be the gcd of the two positive integers x and y.
CANNOT be the gcd of the two positive integers x and y.
Algebraically, since ![]() ,
, ![]() . Also, since
. Also, since ![]() ,
, ![]() . The greatest divisor of x is x, so
. The greatest divisor of x is x, so ![]() cannot be a divisor of x. Likewise, the greatest divisor of y is y, so
cannot be a divisor of x. Likewise, the greatest divisor of y is y, so ![]() cannot be a divisor of y. Therefore,
cannot be a divisor of y. Therefore, ![]() cannot be a divisor of either x or yand thus cannot be a common divisor of x and y.
cannot be a divisor of either x or yand thus cannot be a common divisor of x and y.
The correct answer is E.
106. Last year Carlos saved 10 percent of his annual earnings. This year he earned 5 percent more than last year and he saved 12 percent of his annual earnings. The amount saved this year was what percent of the amount saved last year?
1. (A) 122%
2. (B) 124%
3. (C) 126%
4. (D) 128%
5. (E) 130%
Arithmetic Percents
Let x represent the amount of Carlos”s annual earnings last year.
Carlos”s savings last year ![]() Carlos”s earnings this year
Carlos”s earnings this year ![]() Carlos”s savings this year
Carlos”s savings this year ![]() The amount saved this year as a percent of the amount saved last year is
The amount saved this year as a percent of the amount saved last year is 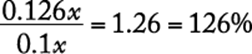 .
.
The correct answer is C.
107. A corporation that had $115.19 billion in profits for the year paid out $230.10 million in employee benefits. Approximately what percent of the profits were the employee benefits? (Note: ![]() )
)
1. (A) 50%
2. (B) 20%
3. (C) 5%
4. (D) 2%
5. (E) 0.2%
Arithmetic Percents; Estimation
The employee benefits as a fraction of profits can be expressed as
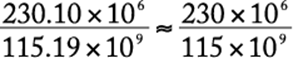
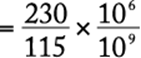
![]()
![]()
![]()
The correct answer is E.
108. In the coordinate plane, line k passes through the origin and has slope 2. If points (3,y) and (x,4) are on line k, then ![]()
1. (A) 3.5
2. (B) 7
3. (C) 8
4. (D) 10
5. (E) 14
Algebra Simple coordinate geometry
Since line k has slope 2 and passes through the origin, the equation of line k is ![]() . If the point (3,y) is on line k, then
. If the point (3,y) is on line k, then ![]() . If the point (x,4) is on line k, then
. If the point (x,4) is on line k, then ![]() and so
and so ![]() . Therefore,
. Therefore, ![]() .
.
The correct answer is C.
109. If a, b, and c are constants, ![]() , and
, and ![]() for all numbers x, what is the value of b?
for all numbers x, what is the value of b?
1. (A) −3
2. (B) −1
3. (C) 0
4. (D) 1
5. (E) 3
Algebra Simplifying algebraic expressions
Since ![]()
![]() then a, b, and c are 0, 1, and −1 in some order. Since
then a, b, and c are 0, 1, and −1 in some order. Since ![]() , it follows that
, it follows that ![]() ,
, ![]() , and
, and ![]() .
.
The correct answer is C.
110. On the number line, if ![]() , if p is halfway between r and s, and if t is halfway between p and r, then
, if p is halfway between r and s, and if t is halfway between p and r, then ![]()
1. (A) ![]()
2. (B) ![]()
3. (C) ![]()
4. (D) 3
5. (E) 4
Algebra Factoring; Simplifying algebraic expressions
Using a number line makes it possible to see these relationships more readily:

The given relative distances between r, s, t, and p are shown in the number line above. The distance between s and t can be expressed as ![]() , or as
, or as ![]() . The distance between t and r can be expressed as
. The distance between t and r can be expressed as ![]() , or as x. Thus, by substitution into the given equation:
, or as x. Thus, by substitution into the given equation:
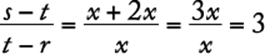 .
.
The correct answer is D.
111. Company K”s earnings were $12 million last year. If this year”s earnings are projected to be 150 percent greater than last year”s earnings, what are Company K”s projected earnings this year?
1. (A) $13.5 million
2. (B) $15 million
3. (C) $18 million
4. (D) $27 million
5. (E) $30 million
Arithmetic Percents
If one quantity x is p percent greater than another quantity y, then 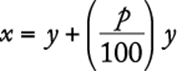 . Let y represent last year”s earnings and x represent this year”s earnings, which are projected to be 150 percent greater than last year”s earnings. Then,
. Let y represent last year”s earnings and x represent this year”s earnings, which are projected to be 150 percent greater than last year”s earnings. Then, 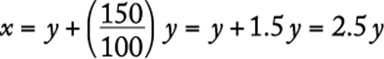 . Since last year”s earnings were $12 million, this year”s earnings are projected to be
. Since last year”s earnings were $12 million, this year”s earnings are projected to be ![]() .
.
The correct answer is E.
112. If ![]() and
and ![]() , then
, then 
1. (A) ![]()
2. (B) ![]()
3. (C) ![]()
4. (D) ![]()
5. (E) 5
Algebra First-degree equations; Simplifying algebraic expressions
Solving  and
and 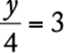 for x and y, respectively, gives
for x and y, respectively, gives 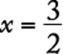 and
and ![]() . Then substituting these into the given expression gives
. Then substituting these into the given expression gives
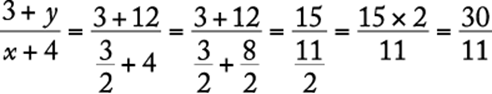
The correct answer is D.
113. ![]()
1. (A) 177
2. (B) 173(18)
3. (C) 176(18)
4. (D) ![]()
5. (E) ![]()
Arithmetic Exponents
Since ![]() and
and ![]() , then 173 may be factored out of each term. It follows that
, then 173 may be factored out of each term. It follows that ![]() .
.
The correct answer is B.
114. A certain clock marks every hour by striking a number of times equal to the hour, and the time required for a stroke is exactly equal to the time interval between strokes. At 6:00 the time lapse between the beginning of the first stroke and the end of the last stroke is 22 seconds. At 12:00, how many seconds elapse between the beginning of the first stroke and the end of the last stroke?
1. (A) 72
2. (B) 50
3. (C) 48
4. (D) 46
5. (E) 44
Arithmetic Operations on rational numbers
At 6:00 there are 6 strokes and 5 intervals between strokes. Thus, there are 11 equal time intervals in the 22 seconds between the beginning of the first stroke and the end of the last stroke.
Therefore, each time interval is 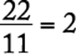 seconds long. At 12:00 there are 12 strokes and 11 intervals between strokes. Thus, there are 23 equal 2-second time intervals, or
seconds long. At 12:00 there are 12 strokes and 11 intervals between strokes. Thus, there are 23 equal 2-second time intervals, or ![]() seconds, between the beginning of the first stroke and the end of the last stroke.
seconds, between the beginning of the first stroke and the end of the last stroke.
The correct answer is D.
115. What is the greatest number of identical bouquets that can be made out of 21 white and 91 red tulips if no flowers are to be left out? (Two bouquets are identical whenever the number of red tulips in the two bouquets is equal and the number of white tulips in the two bouquets is equal.)
1. (A) 3
2. (B) 4
3. (C) 5
4. (D) 6
5. (E) 7
Arithmetic Properties of numbers
Since the question asks for the greatest number of bouquets that can be made using all of the flowers, the number of bouquets will need to be the greatest common factor of 21 and 91. Since ![]() and
and ![]() , the greatest common factor of 21 and 91 is 7. Therefore, 7 bouquets can be made, each with 3 white tulips and 13 red tulips.
, the greatest common factor of 21 and 91 is 7. Therefore, 7 bouquets can be made, each with 3 white tulips and 13 red tulips.
The correct answer is E.
116. In the xy-plane, the points (c,d), (c,−d), and (−c,−d) are three vertices of a certain square. If c < 0 and d > 0, which of the following points is in the same quadrant as the fourth vertex of the square?
1. (A) (−5,−3)
2. (B) (−5,3)
3. (C) (5,−3)
4. (D) (3,−5)
5. (E) (3,5)
Geometry Coordinate geometry
Because the points (c,d) and (c,−d) lie on the same vertical line (the line with equation x = c), one side of the square has length 2d and is vertical. Therefore, the side of the square opposite this side has length 2d, is vertical, and contains the vertex (−c,−d). From this it follows that the remaining vertex is (−c,d), because (−c,d) lies on the same vertical line as (−c,−d) (the line with equation x = −c) and these two vertices are a distance 2d apart. Because c < 0 and d > 0, the point (−c,d) has positive x-coordinate and positivey-coordinate. Thus, the point (−c,d) is in Quadrant I. Of the answer choices, only (3,5) is in Quadrant I.
The correct answer is E.
117. For all numbers s and t, the operation ![]() is defined by
is defined by ![]() . If
. If ![]() , then
, then ![]()
1. (A) 2
2. (B) 3
3. (C) 5
4. (D) 6
5. (E) 11
Algebra First-degree equations
The equivalent values established for this problem are ![]() and
and ![]() . So, substitute −2 for s and x for t in the given equation:
. So, substitute −2 for s and x for t in the given equation:
![]()
![]()
![]()
![]()
![]()
The correct answer is B.
118. Salesperson A”s compensation for any week is $360 plus 6 percent of the portion of A”s total sales above $1,000 for that week. Salesperson B”s compensation for any week is 8 percent of B”s total sales for that week. For what amount of total weekly sales would both salespeople earn the same compensation?
1. (A) $21,000
2. (B) $18,000
3. (C) $15,000
4. (D) $4,500
5. (E) $4,000
Algebra Applied problems; Simultaneous equations
Let x represent the total weekly sales amount at which both salespersons earn the same compensation. Then, the given information regarding when Salesperson A”s weekly pay equals Salesperson B”s weekly pay can be expressed as:
|
|
|
|
|
solve for x |
|
|
|
|
|
The correct answer is C.
119. If 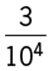 = x%, then x =
= x%, then x =
1. (A) 0.3
2. (B) 0.03
3. (C) 0.003
4. (D) 0.0003
5. (E) 0.00003
Arithmetic Percents
Given that ![]() , and writing x% as
, and writing x% as ![]() , it follows that
, it follows that ![]() . Multiplying both sides by 100 gives
. Multiplying both sides by 100 gives ![]()
The correct answer is B.
120. If a basketball team scores an average (arithmetic mean) of x points per game for n games and then scores y points in its next game, what is the team”s average score for the ![]() games?
games?
1. (A) ![]()
2. (B) ![]()
3. (C) ![]()
4. (D) 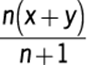
5. (E) ![]()
Arithmetic Statistics
Using the formula average 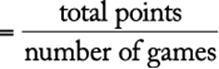 , the average number of points per game for the first n games can be expressed as
, the average number of points per game for the first n games can be expressed as 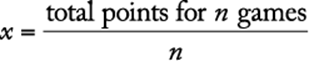 . Solving this equation shows that the total points for n games
. Solving this equation shows that the total points for n games ![]() . Then, the total points for
. Then, the total points for ![]() games can be expressed as
games can be expressed as ![]() , and the average number of points for
, and the average number of points for ![]() games
games 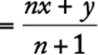 .
.
The correct answer is A.
121. If ![]() and
and ![]() , which of the following must be negative?
, which of the following must be negative?
1. (A) xyz
2. (B) xyz2
3. (C) xy2z
4. (D) xy2z2
5. (E) x2y2z2
Arithmetic Properties of numbers
Since ![]() and
and ![]() ,
, ![]() , and xy2z is the expression given in answer choice C. Alternatively, the chart below shows all possibilities for the algebraic signs of x, y, and z. Those satisfying
, and xy2z is the expression given in answer choice C. Alternatively, the chart below shows all possibilities for the algebraic signs of x, y, and z. Those satisfying ![]() are checked in the fourth column of the chart, and those satisfying
are checked in the fourth column of the chart, and those satisfying ![]() are checked in the fifth column of the chart.
are checked in the fifth column of the chart.
|
x |
y |
z |
|
|
|
+ |
+ |
+ |
|
|
|
+ |
+ |
− |
|
|
|
+ |
− |
+ |
|
|
|
+ |
− |
− |
||
|
− |
+ |
+ |
||
|
− |
+ |
− |
|
|
|
− |
− |
+ |
|
|
|
− |
− |
− |
|
The chart below shows only the possibilities that satisfy both ![]() and
and ![]() . Noting that the expression in answer choice E is the product of the squares of three nonzero numbers, which is always positive, extend the chart to include the algebraic sign of each of the other answer choices.
. Noting that the expression in answer choice E is the product of the squares of three nonzero numbers, which is always positive, extend the chart to include the algebraic sign of each of the other answer choices.
|
x |
y |
z |
xyz |
xyz2 |
xy2z |
xy2z2 |
|
+ |
+ |
− |
− |
+ |
− |
+ |
|
− |
− |
+ |
+ |
+ |
− |
− |
Only xy2z is negative in both cases.
The correct answer is C.
122. At a certain pizzeria, ![]() of the pizzas sold in one week were mushroom and
of the pizzas sold in one week were mushroom and ![]() of the remaining pizzas sold were pepperoni. If n of the pizzas sold were pepperoni, how many were mushroom?
of the remaining pizzas sold were pepperoni. If n of the pizzas sold were pepperoni, how many were mushroom?
1. (A) ![]()
2. (B) ![]()
3. (C) ![]()
4. (D) ![]()
5. (E) 3n
Algebra Simplifying algebraic expressions
Let t represent the total number of pizzas sold. Then ![]() represents the number of mushroom pizzas sold,
represents the number of mushroom pizzas sold, ![]() represents the number of remaining pizzas sold, and
represents the number of remaining pizzas sold, and 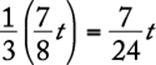 represents the number of pepperoni pizzas sold. Then
represents the number of pepperoni pizzas sold. Then 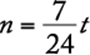 ,
, 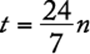 , and
, and 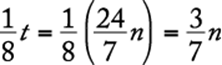 . Thus,
. Thus, ![]() mushroom pizzas were sold.
mushroom pizzas were sold.
The correct answer is B.
123. Two trains, X and Y, started simultaneously from opposite ends of a 100-mile route and traveled toward each other on parallel tracks. Train X, traveling at a constant rate, completed the 100-mile trip in 5 hours; Train Y, traveling at a constant rate, completed the 100-mile trip in 3 hours. How many miles had Train X traveled when it met Train Y?
1. (A) 37.5
2. (B) 40.0
3. (C) 60.0
4. (D) 62.5
5. (E) 77.5
Algebra Applied problems
To solve this problem, use the formula distance = rate × time and its two equivalent forms  and
and  . Train X traveled 100 miles in 5 hours so its rate was
. Train X traveled 100 miles in 5 hours so its rate was 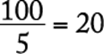 miles per hour. Train Y traveled 100 miles in 3 hours so its rate was
miles per hour. Train Y traveled 100 miles in 3 hours so its rate was ![]() miles per hour. If t represents the number of hours the trains took to meet, then when the trains met, Train X had traveled a distance of 20t miles and Train Y had traveled a distance of
miles per hour. If t represents the number of hours the trains took to meet, then when the trains met, Train X had traveled a distance of 20t miles and Train Y had traveled a distance of 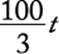 miles.
miles.
Since the trains started at opposite ends of the 100-mile route, the sum of the distances they had traveled when they met was 100 miles. Therefore,
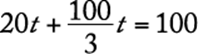
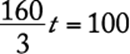
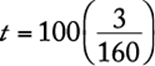
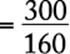
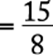
Thus, Train X had traveled 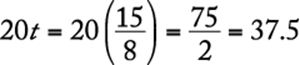 miles when it met Train Y.
miles when it met Train Y.
The correct answer is A.
124. What is the value of ![]() for
for ![]() ?
?
1. (A) − 0.72
2. (B) − 1.42
3. (C) − 1.98
4. (D) − 2.40
5. (E) − 2.89
Algebra Simplifying algebraic expressions
Work the problem by substituting ![]() .
.
![]()
![]()
![]()
![]()
![]()
The correct answer is D.
125. What is the remainder when 324 is divided by 5?
1. (A) 0
2. (B) 1
3. (C) 2
4. (D) 3
5. (E) 4
Arithmetic Properties of numbers
A pattern in the units digits of the numbers 3, 32 = 9, 33 = 27, 34 = 81, 35 = 243, etc., can be found by observing that the units digit of a product of two integers is the same as the units digit of the product of the units digit of the two integers. For example, the units digit of 35 = 3 × 34 = 3 × 81 is 3 since the units digit of 3 × 1 is 3, and the units digit of 36 = 3 × 35 = 3 × 243 is 9 since the units digit of 3 × 3 is 9. From this it follows that the units digit of the powers of 3 follow the pattern 3, 9, 7, 1, 3, 9, 7, 1, etc., with a units digit of 1 for 34, 38, 312, . . . , 324, . . . . Therefore, the units digit of 324 is 1. Thus, 324 is 1 more than a multiple of 10, and hence 324 is 1 more than a multiple of 5, and so the remainder when 324 is divided by 5 is 1.
The correct answer is B.
126. If the volume of a ball is 32,490 cubic millimeters, what is the volume of the ball in cubic centimeters? (1 millimeter = 0.1 centimeter)
1. (A) 0.3249
2. (B) 3.249
3. (C) 32.49
4. (D) 324.9
5. (E) 3,249
Arithmetic Measurement conversion
Since 1 mm = 0.1 cm, it follows that 1 mm3 = (0.1)3 cm3 = 0.001 cm3. Therefore, 32,490 mm3 = (32,490)(0.001) cm3 = 32.49 cm3.
The correct answer is C.
127. David used part of $100,000 to purchase a house. Of the remaining portion, he invested ![]() of it at 4 percent simple annual interest and
of it at 4 percent simple annual interest and ![]() of it at 6 percent simple annual interest. If after a year the income from the two investments totaled $320, what was the purchase price of the house?
of it at 6 percent simple annual interest. If after a year the income from the two investments totaled $320, what was the purchase price of the house?
1. (A) $96,000
2. (B) $94,000
3. (C) $88,000
4. (D) $75,000
5. (E) $40,000
Algebra Applied problems; Percents
Let x be the amount, in dollars, that David used to purchase the house. Then David invested (100,000 − x) dollars, ![]() at 4% simple annual interest and
at 4% simple annual interest and ![]() at 6% simple annual interest. After one year the total interest, in dollars, on this investment was
at 6% simple annual interest. After one year the total interest, in dollars, on this investment was ![]() (100,000 −x)(0.04) +
(100,000 −x)(0.04) + ![]() (100,000 − x)(0.06) = 320. Solve this equation to find the value of x.
(100,000 − x)(0.06) = 320. Solve this equation to find the value of x.
|
|
given |
|
(100,000 − x)(0.04) + 2(100,000 − x)(0.06) = 960 |
multiply both sides by 3 |
|
4,000 − 0.04x + 12,000 − 0.12x = 960 |
distributive property |
|
16,000 − 0.16x = 960 |
combine like terms |
|
16,000 − 960 = 0.16x |
add 0.16x − 960 to both sides |
|
100,000 − 6,000 = x |
divide both sides by 0.16 |
|
94,000 = x |
Therefore, the purchase price of the house was $94,000.
The correct answer is B.
128. The cost to rent a small bus for a trip is x dollars, which is to be shared equally among the people taking the trip. If 10 people take the trip rather than 16, how many more dollars, in terms of x, will it cost per person?
1. (A) ![]()
2. (B) ![]()
3. (C) ![]()
4. (D) ![]()
5. (E) ![]()
Algebra Applied problems
If 16 take the trip, the cost per person would be ![]() dollars. If 10 take the trip, the cost per person would be
dollars. If 10 take the trip, the cost per person would be ![]() dollars. (Note that the lowest common multiple of 10 and 16 is 80.)
dollars. (Note that the lowest common multiple of 10 and 16 is 80.)
Thus, if 10 take the trip, the increase in dollars per person would be 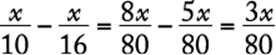 .
.
The correct answer is E.
129. If x is an integer and ![]() , which of the following CANNOT be a divisor of y?
, which of the following CANNOT be a divisor of y?
1. (A) 4
2. (B) 5
3. (C) 6
4. (D) 7
5. (E) 8
Arithmetic Properties of numbers
Although 3x is always divisible by 3, ![]() cannot be divisible by 3 since 2 is not divisible by 3. Thus,
cannot be divisible by 3 since 2 is not divisible by 3. Thus, ![]() cannot be divisible by any multiple of 3, including 6.
cannot be divisible by any multiple of 3, including 6.
The correct answer is C.
130. A certain electronic component is sold in boxes of 54 for $16.20 and in boxes of 27 for $13.20. A customer who needed only 54 components for a project had to buy 2 boxes of 27 because boxes of 54 were unavailable. Approximately how much more did the customer pay for each component due to the unavailability of the larger boxes?
1. (A) $0.33
2. (B) $0.19
3. (C) $0.11
4. (D) $0.06
5. (E) $0.03
Arithmetic Operations of rational numbers
The customer paid ![]() for the 2 boxes of 27 components. This is
for the 2 boxes of 27 components. This is ![]() more than the cost of a single box of 54 components. So, the extra cost per component is
more than the cost of a single box of 54 components. So, the extra cost per component is 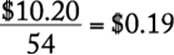 .
.
The correct answer is B.
131. As a salesperson, Phyllis can choose one of two methods of annual payment: either an annual salary of $35,000 with no commission or an annual salary of $10,000 plus a 20 percent commission on her total annual sales. What must her total annual sales be to give her the same annual pay with either method?
1. (A) $100,000
2. (B) $120,000
3. (C) $125,000
4. (D) $130,000
5. (E) $132,000
Algebra Applied problems
Letting s be Phyllis”s total annual sales needed to generate the same annual pay with either method, the given information can be expressed as ![]() . Solve this equation for s.
. Solve this equation for s.
![]()
![]()
![]()
The correct answer is C.
132. Last year Department Store X had a sales total for December that was 4 times the average (arithmetic mean) of the monthly sales totals for January through November. The sales total for December was what fraction of the sales total for the year?
1. (A) ![]()
2. (B) ![]()
3. (C) ![]()
4. (D) ![]()
5. (E) ![]()
Algebra; Arithmetic Applied problems; Statistics
Let A equal the average sales per month for the first 11 months. The given information about the total sales for the year can then be expressed as ![]() . Thus,
. Thus, ![]() , where F is the fraction of the sales total for the year that the sales total for December represents. Then
, where F is the fraction of the sales total for the year that the sales total for December represents. Then 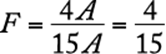 .
.
The correct answer is B.
133. Working alone, Printers X, Y, and Z can do a certain printing job, consisting of a large number of pages, in 12, 15, and 18 hours, respectively. What is the ratio of the time it takes Printer X to do the job, working alone at its rate, to the time it takes Printers Y and Z to do the job, working together at their individual rates?
1. (A) ![]()
2. (B) ![]()
3. (C) ![]()
4. (D) ![]()
5. (E) ![]()
Arithmetic Operations on rational numbers
Since Printer Y can do the job in 15 hours, it can do ![]() of the job in 1 hour. Since Printer Z can do the job in 18 hours, it can do
of the job in 1 hour. Since Printer Z can do the job in 18 hours, it can do ![]() of the job in 1 hour. Together, Printers Y and Z can do
of the job in 1 hour. Together, Printers Y and Z can do 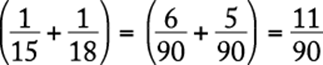 of the job in 1 hour, which means that it takes them
of the job in 1 hour, which means that it takes them ![]() hours to complete the job. Since Printer X completes the job in 12 hours, the ratio of the time required for X to do the job to the time required for Y and Z working together to do the job is
hours to complete the job. Since Printer X completes the job in 12 hours, the ratio of the time required for X to do the job to the time required for Y and Z working together to do the job is 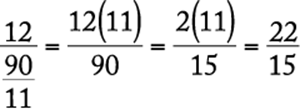 .
.
The correct answer is D.
134. In the sequence x0, x1, x2, . . . , xn, each term from x1 to xk is 3 greater than the previous term, and each term from ![]() to xn is 3 less than the previous term, where n and k are positive integers and
to xn is 3 less than the previous term, where n and k are positive integers and ![]() . If
. If ![]() and if
and if ![]() , what is the value of n?
, what is the value of n?
1. (A) 5
2. (B) 6
3. (C) 9
4. (D) 10
5. (E) 15
Algebra Sequences
Since ![]() and each term from x1 to xk is 3 greater than the previous term, then
and each term from x1 to xk is 3 greater than the previous term, then ![]() . Since
. Since ![]() , then
, then ![]() and
and ![]() . Since each term from
. Since each term from ![]() to xn is 3 less than the previous term, then
to xn is 3 less than the previous term, then ![]() . Substituting the known values for xk, xn, and k gives
. Substituting the known values for xk, xn, and k gives ![]() , from which it follows that
, from which it follows that ![]() and
and ![]() .
.
The correct answer is D.
135. If ![]() , then
, then 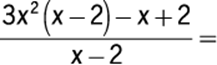
1. (A) ![]()
2. (B) ![]()
3. (C) 3x2
4. (D) ![]()
5. (E) ![]()
Algebra Simplifying algebraic expressions
When simplifying this expression, it is important to note that, as a first step, the numerator must be factored so that the numerator is the product of two or more expressions, one of which is ![]() . This can be accomplished by rewriting the last two terms of the numerator as
. This can be accomplished by rewriting the last two terms of the numerator as ![]() . Then
. Then
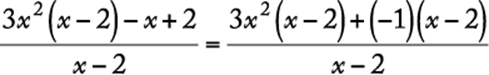
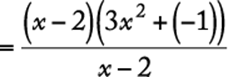
![]()
![]()
The correct answer is D.
136. In the figure shown above, line segment QR has length 12, and rectangle MPQT is a square. If the area of rectangular region MPRS is 540, what is the area of rectangular region TQRS?
1. (A) 144
2. (B) 216
3. (C) 324
4. (D) 360
5. (E) 396
Geometry; Algebra Area; Second-degree equations
Since MPQT is a square, let ![]() . Then
. Then ![]() . The area of MPRS can be expressed as
. The area of MPRS can be expressed as ![]() . Since the area of MPRS is given to be 540,
. Since the area of MPRS is given to be 540,
![]()
![]()
![]()
![]()
![]() or
or ![]()
Since x represents a length and must be positive, ![]() . The area of TQRS is then
. The area of TQRS is then ![]() . As an alternative to solving the quadratic equation, look for a pair of positive numbers such that their product is 540 and one is 12 greater than the other. The pair is 18 and 30, so
. As an alternative to solving the quadratic equation, look for a pair of positive numbers such that their product is 540 and one is 12 greater than the other. The pair is 18 and 30, so ![]() and the area of TQRS is then
and the area of TQRS is then ![]() .
.
The correct answer is B.
137. A train travels from New York City to Chicago, a distance of approximately 840 miles, at an average rate of 60 miles per hour and arrives in Chicago at 6:00 in the evening, Chicago time. At what hour in the morning, New York City time, did the train depart for Chicago? (Note: Chicago time is one hour earlier than New York City time.)
1. (A) 4:00
2. (B) 5:00
3. (C) 6:00
4. (D) 7:00
5. (E) 8:00
Arithmetic Operations on rational numbers
Using the formula 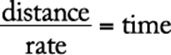 , it can be calculated that it took the train
, it can be calculated that it took the train 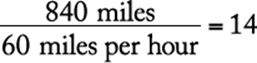 hours to travel from New York City to Chicago. The train arrived in Chicago at 6:00 in the evening. Since it had departed 14 hours before that, it had therefore departed at 4:00 a.m. Chicago time. Then, since it is given that Chicago time is one hour earlier than New York City time, it had departed at 5:00 a.m. New York City time.
hours to travel from New York City to Chicago. The train arrived in Chicago at 6:00 in the evening. Since it had departed 14 hours before that, it had therefore departed at 4:00 a.m. Chicago time. Then, since it is given that Chicago time is one hour earlier than New York City time, it had departed at 5:00 a.m. New York City time.
The correct answer is B.
138. Last year Manfred received 26 paychecks. Each of his first 6 paychecks was $750; each of his remaining paychecks was $30 more than each of his first 6 paychecks. To the nearest dollar, what was the average (arithmetic mean) amount of his paychecks for the year?
1. (A) $752
2. (B) $755
3. (C) $765
4. (D) $773
5. (E) $775
Arithmetic Statistics
In addition to the first 6 paychecks for $750 each, Manfred received ![]() paychecks for
paychecks for ![]() or $780 each. Applying the formula
or $780 each. Applying the formula  average, this information can be expressed in the following equation:
average, this information can be expressed in the following equation:
The correct answer is D.
139. Machines A and B always operate independently and at their respective constant rates. When working alone, Machine A can fill a production lot in 5 hours, and Machine B can fill the same lot in x hours. When the two machines operate simultaneously to fill the production lot, it takes them 2 hours to complete the job. What is the value of x?
1. (A) ![]()
2. (B) 3
3. (C) ![]()
4. (D) ![]()
5. (E) ![]()
Algebra Applied problems
Since Machine A can fill a production lot in 5 hours, it can fill ![]() of the lot in 1 hour. Since Machine B can fill the same production lot in x hours, it can fill
of the lot in 1 hour. Since Machine B can fill the same production lot in x hours, it can fill ![]() of the lot in 1 hour. The two machines operating simultaneously can fill
of the lot in 1 hour. The two machines operating simultaneously can fill 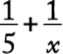 of the lot in 1 hour. Since it takes them 2 hours to complete the lot together, they can fill
of the lot in 1 hour. Since it takes them 2 hours to complete the lot together, they can fill ![]() of the lot in 1 hour and so
of the lot in 1 hour and so 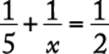 , which can be solved for x as follows:
, which can be solved for x as follows:
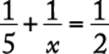
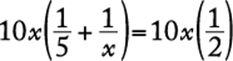
![]()
![]()
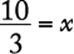
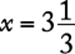
The correct answer is A.
140. A driver completed the first 20 miles of a 40-mile trip at an average speed of 50 miles per hour. At what average speed must the driver complete the remaining 20 miles to achieve an average speed of 60 miles per hour for the entire 40-mile trip? (Assume that the driver did not make any stops during the 40-mile trip.)
1. (A) 65 mph
2. (B) 68 mph
3. (C) 70 mph
4. (D) 75 mph
5. (E) 80 mph
Algebra Applied problems
Using ![]() , where D represents distance, r represents average speed, and t represents time, and its equivalent formula
, where D represents distance, r represents average speed, and t represents time, and its equivalent formula 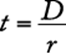 to make a chart like the one below is often helpful in solving this type of problem.
to make a chart like the one below is often helpful in solving this type of problem.
|
D |
r |
t |
|
|
1st 20 miles |
20 |
50 |
|
|
2nd 20 miles |
20 |
r |
|
|
Total trip |
40 |
60 |
|
The total time for the trip is the sum of the times for the first 20 miles and the second 20 miles, so
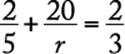
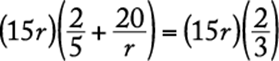
![]()
![]()
![]()
The correct answer is D.

141. The figure shown above consists of three identical circles that are tangent to each other. If the area of the shaded region is ![]() , what is the radius of each circle?
, what is the radius of each circle?
1. (A) 4
2. (B) 8
3. (C) 16
4. (D) 24
5. (E) 32
Geometry Circles; Triangles; Area
Let r represent the radius of each circle. Then the triangle shown dashed in the figure is equilateral with sides 2r units long. The interior of the triangle is composed of the shaded region and three circular sectors. The area of the shaded region can be found as the area of the triangle minus the sum of the areas of the three sectors. Since the triangle is equilateral, its side lengths are in the proportions as shown in the following diagram. The area of the interior of the triangle is 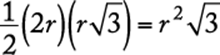 .
.
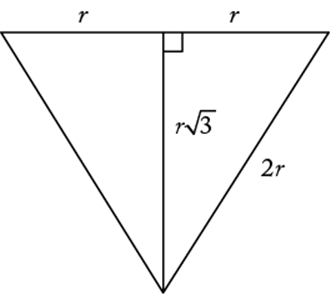
Each of the three sectors has a central angle of ![]() because the central angle is an angle of the equilateral triangle. Therefore, the area of each sector is
because the central angle is an angle of the equilateral triangle. Therefore, the area of each sector is 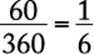 of the area of the circle. The sum of the areas of the three sectors is then
of the area of the circle. The sum of the areas of the three sectors is then 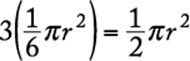 . Thus, the area of the shaded region is
. Thus, the area of the shaded region is 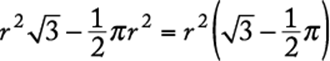 . But, this area is given as
. But, this area is given as 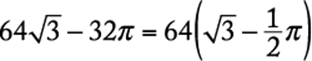 . Thus
. Thus ![]() , and
, and ![]() .
.
The correct answer is B.
142. A positive integer n is a perfect number provided that the sum of all the positive factors of n, including 1 and n, is equal to 2n. What is the sum of the reciprocals of all the positive factors of the perfect number 28?
1. (A) ![]()
2. (B) ![]()
3. (C) 2
4. (D) 3
5. (E) 4
Arithmetic Properties of numbers
The factors of 28 are 1, 2, 4, 7, 14, and 28. Therefore, the sum of the reciprocals of the factors of 28 is ![]() =
= ![]() =
= ![]() =
= ![]() = 2.
= 2.
The correct answer is C.
143. The infinite sequence a1, a2, . . . , an, . . . is such that a1 = 2, a2 = −3, a3 = 5, a4 = −1, and an = an− 4 for n > 4. What is the sum of the first 97 terms of the sequence?
1. (A) 72
2. (B) 74
3. (C) 75
4. (D) 78
5. (E) 80
Arithmetic Sequences and series
Because an = an − 4 for n > 4, it follows that the terms of the sequence repeat in groups of 4 terms:
|
Values for n |
Values for an |
|
1, 2, 3, 4 |
2, −3, 5, −1 |
|
5, 6, 7, 8 |
2, −3, 5, −1 |
|
9, 10, 11, 12 |
2, −3, 5, −1 |
|
13, 14, 15, 16 |
2, −3, 5, −1 |
Thus, since 97 = 24(4) + 1, the sum of the first 97 terms can be grouped into 24 groups of 4 terms each, with one remaining term, which allows the sum to be easily found:
(a1 + a2 + a3 + a4) + (a5 + a6 + a7 + a8) + . . . + (a93 + a94 + a95 + a96) + a97
= (2 − 3 + 5 − 1) + (2 − 3 + 5 − 1) + . . . + (2 − 3 + 5 − 1) + 2
= 24(2 − 3 + 5 − 1) + 2 = 24(3) + 2 = 74
The correct answer is B.
144. The sequence a1, a2, . . . , an, . . . is such that an = 2an − 1 − x for all positive integers n ≥ 2 and for a certain number x. If a5 = 99 and a3 = 27, what is the value of x?
1. (A) 3
2. (B) 9
3. (C) 18
4. (D) 36
5. (E) 45
Algebra Sequences and series
An expression for a5 that involves x can be obtained using a3 = 27 and applying the equation an = 2an − 1 − x twice, once for n = 4 and once for n = 5.
|
a4 = 2a3 − x |
using an = 2an − 1 − x for n = 4 |
|
= 2(27) − x |
using a3 = 27 |
|
a5 = 2a4 − x |
using an = 2an − 1 − x for n = 5 |
|
= 2[2(27) − x] − x |
using a4 = 2(27) − x |
|
= 4(27) − 3x |
combine like terms |
Therefore, using a5 = 99, we have
|
99 = 4(27) − 3x |
given |
|
3x = 4(27) − 99 |
adding (3x − 99) to both sides |
|
x = 4(9) − 33 |
dividing both sides by 3 |
|
x = 3 |
arithmetic |
The correct answer is A.
145. A window is in the shape of a regular hexagon with each side of length 80 centimeters. If a diagonal through the center of the hexagon is w centimeters long, then w =
1. (A) 80
2. (B) 120
3. (C) 150
4. (D) 160
5. (E) 240
Geometry Polygons
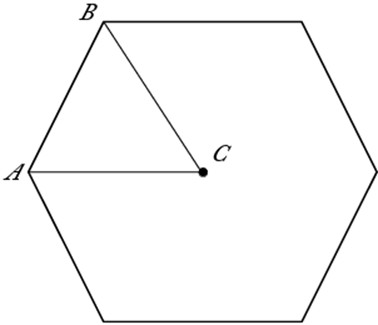
Let A and B be the endpoints of one of the sides of the hexagon and let C be the center of the hexagon. Then the degree measure of ![]() ACB is
ACB is ![]() = 60 and the sum of the degree measures of
= 60 and the sum of the degree measures of ![]() ABC and
ABC and ![]() BAC is 180 − 60 = 120. Also, since AC = BC, the degree measures of
BAC is 180 − 60 = 120. Also, since AC = BC, the degree measures of ![]() ABC and
ABC and ![]() BAC are equal. Therefore, the degree measure of each of
BAC are equal. Therefore, the degree measure of each of ![]() ABC and
ABC and ![]() BAC is 60. Thus, ΔABC is an equilateral triangle with side length AB = 80. It follows that the length of a diagonal through the center of the hexagon is 2(AC) = 2(80) = 160.
BAC is 60. Thus, ΔABC is an equilateral triangle with side length AB = 80. It follows that the length of a diagonal through the center of the hexagon is 2(AC) = 2(80) = 160.
The correct answer is D.
146. On a certain transatlantic crossing, 20 percent of a ship”s passengers held round-trip tickets and also took their cars aboard the ship. If 60 percent of the passengers with round-trip tickets did not take their cars aboard the ship, what percent of the ship”s passengers held round-trip tickets?
1. (A) 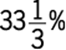
2. (B) 40%
3. (C) 50%
4. (D) 60%
5. (E) 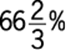
Arithmetic Percents
Since the number of passengers on the ship is immaterial, let the number of passengers on the ship be 100 for convenience. Let x be the number of passengers that held round-trip tickets. Then, since 20 percent of the passengers held a round-trip ticket and took their cars aboard the ship, ![]() passengers held round-trip tickets and took their cars aboard the ship. The remaining passengers with round-trip tickets did not take their cars aboard, and they represent 0.6x (that is, 60 percent of the passengers with round-trip tickets). Thus,
passengers held round-trip tickets and took their cars aboard the ship. The remaining passengers with round-trip tickets did not take their cars aboard, and they represent 0.6x (that is, 60 percent of the passengers with round-trip tickets). Thus, ![]() , from which it follows that
, from which it follows that ![]() , and so
, and so ![]() . The percent of passengers with round-trip tickets is, then,
. The percent of passengers with round-trip tickets is, then, 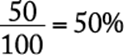 .
.
The correct answer is C.
147. If x and k are integers and ![]() , what is the value of k?
, what is the value of k?
1. (A) 5
2. (B) 7
3. (C) 10
4. (D) 12
5. (E) 14
Arithmetic Exponents
Rewrite the expression on the left so that it is a product of powers of 2 and 3.
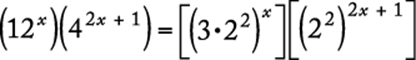
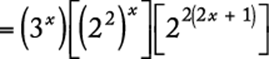
![]()
![]()
Then, since ![]() , it follows that
, it follows that ![]() , so
, so ![]() and
and ![]() . Substituting 2 for x gives
. Substituting 2 for x gives ![]() .
.
The correct answer is E.
148. For every even positive integer m, f(m) represents the product of all even integers from 2 to m, inclusive. For example, ![]() . What is the greatest prime factor of f(24)?
. What is the greatest prime factor of f(24)?
1. (A) 23
2. (B) 19
3. (C) 17
4. (D) 13
5. (E) 11
Arithmetic Properties of numbers
Rewriting ![]()
![]()
![]() shows that all of the prime numbers from 2 through 11 are factors of f(24). The next prime number is 13, but 13 is not a factor of f(24) because none of the even integers from 2 through 24 has 13 as a factor. Therefore, the largest prime factor of f(24) is 11.
shows that all of the prime numbers from 2 through 11 are factors of f(24). The next prime number is 13, but 13 is not a factor of f(24) because none of the even integers from 2 through 24 has 13 as a factor. Therefore, the largest prime factor of f(24) is 11.
The correct answer is E.
149. In pentagon PQRST, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . Which of the lengths 5, 10, and 15 could be the value of PT?
. Which of the lengths 5, 10, and 15 could be the value of PT?
1. (A) 5 only
2. (B) 15 only
3. (C) 5 and 10 only
4. (D) 10 and 15 only
5. (E) 5, 10, and 15
Geometry Polygons; Triangles
In the figure above, diagonals ![]() and
and ![]() have been drawn in to show
have been drawn in to show ![]() and
and ![]() . Because the length of any side of a triangle must be less than the sum of the lengths of the other two sides,
. Because the length of any side of a triangle must be less than the sum of the lengths of the other two sides, ![]() in
in ![]() , and
, and ![]() in
in ![]() . Since
. Since ![]() , then
, then ![]() , which then implies
, which then implies ![]() . Now,
. Now, ![]() in
in ![]() , and since
, and since ![]() ,
, ![]() . It follows that
. It follows that ![]() . Therefore, 15 cannot be the length of
. Therefore, 15 cannot be the length of ![]() since
since ![]() .
.
To show that 5 can be the length of ![]() , consider the figure above. For
, consider the figure above. For ![]() , the length of any side is less than the sum of the lengths of the other two sides as shown below.
, the length of any side is less than the sum of the lengths of the other two sides as shown below.
![]()
![]()
![]()
For ![]() , the length of any side is less than the sum of the lengths of the other two sides as shown below.
, the length of any side is less than the sum of the lengths of the other two sides as shown below.
![]()
![]()
![]()
For ![]() , the length of any side is less than the sum of the lengths of the other two sides as shown below.
, the length of any side is less than the sum of the lengths of the other two sides as shown below.
![]()
![]()
![]()
To show that 10 can be the length of ![]() , consider the figure above. For
, consider the figure above. For ![]() , the length of any side is less than the sum of the lengths of the other two sides as shown below.
, the length of any side is less than the sum of the lengths of the other two sides as shown below.
![]()
![]()
![]()
For ![]() , the length of any side is less than the sum of the lengths of the other two sides as shown below.
, the length of any side is less than the sum of the lengths of the other two sides as shown below.
![]()
![]()
![]()
For ![]() , the length of any side is less than the sum of the lengths of the other two sides as shown below.
, the length of any side is less than the sum of the lengths of the other two sides as shown below.
![]()
![]()
![]()
Therefore, 5 and 10 can be the length of ![]() , and 15 cannot be the length of
, and 15 cannot be the length of ![]() .
.
The correct answer is C.
3, k, 2, 8, m, 3
150. The arithmetic mean of the list of numbers above is 4. If k and m are integers and ![]() , what is the median of the list?
, what is the median of the list?
1. (A) 2
2. (B) 2.5
3. (C) 3
4. (D) 3.5
5. (E) 4
Arithmetic Statistics
Since the arithmetic mean  , then
, then  , and so
, and so  ,
, ![]() ,
, ![]() . Since
. Since ![]() , then either
, then either ![]() and
and ![]() or
or ![]() and
and ![]() . Because k and m are integers, either
. Because k and m are integers, either ![]() and
and ![]() or
or ![]() and
and ![]() .
.
6. Case (i): If ![]() , then
, then ![]() and the six integers in ascending order are k, 2, 3, 3, m, 8 or k, 2, 3, 3, 8, m. The two middle integers are both 3 so the median is
and the six integers in ascending order are k, 2, 3, 3, m, 8 or k, 2, 3, 3, 8, m. The two middle integers are both 3 so the median is 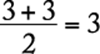 .
.
7. Case (ii): If ![]() , then
, then ![]() and the six integers in ascending order are 2, k, 3, 3, m, 8. The two middle integers are both 3 so the median is
and the six integers in ascending order are 2, k, 3, 3, m, 8. The two middle integers are both 3 so the median is 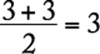 .
.
8. Case (iii): If ![]() , then
, then ![]() and the six integers in ascending order are 2, m, 3, 3, k, 8. The two middle integers are both 3 so the median is
and the six integers in ascending order are 2, m, 3, 3, k, 8. The two middle integers are both 3 so the median is 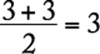 .
.
9. Case (iv): If ![]() , then
, then ![]() and the six integers in ascending order are m, 2, 3, 3, k, 8 or m, 2, 3, 3, 8, k. The two middle integers are both 3 so the median is
and the six integers in ascending order are m, 2, 3, 3, k, 8 or m, 2, 3, 3, 8, k. The two middle integers are both 3 so the median is 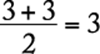 .
.
The correct answer is C.

151. If the variables X, Y, and Z take on only the values 10, 20, 30, 40, 50, 60, or 70 with frequencies indicated by the shaded regions above, for which of the frequency distributions is the mean equal to the median?
1. (A) X only
2. (B) Y only
3. (C) Z only
4. (D) X and Y
5. (E) X and Z
Arithmetic Statistics
The frequency distributions for both X and Z are symmetric about 40, and thus both X and Z have ![]() . Therefore, any answer choice that does not include both X and Z can be eliminated. This leaves only answer choice E.
. Therefore, any answer choice that does not include both X and Z can be eliminated. This leaves only answer choice E.
The correct answer is E.

152. When the figure above is cut along the solid lines, folded along the dashed lines, and taped along the solid lines, the result is a model of a geometric solid. This geometric solid consists of 2 pyramids, each with a square base that they share. What is the sum of the number of edges and the number of faces of this geometric solid?
1. (A) 10
2. (B) 18
3. (C) 20
4. (D) 24
5. (E) 25
Geometry Solids
A geometric solid consisting of 2 pyramids, each with a square base that they share, is shown in the figure above. From the figure it can be seen that the solid has 12 edges and 8 faces. Therefore, the sum of the number of edges and the number of faces of the solid is 12 + 8 = 20.
Alternatively, the solid has 7 + 5 = 12 edges because each edge in the solid is generated from either a dashed segment (there are 7 dashed segments) or from a pair of solid segments taped together (there are ![]() = 5 such pairs of solid segments), and the solid has 8 faces because there are 8 small triangles in the given figure. Therefore, the sum of the number of edges and the number of faces of the solid is 12 + 8 = 20.
= 5 such pairs of solid segments), and the solid has 8 faces because there are 8 small triangles in the given figure. Therefore, the sum of the number of edges and the number of faces of the solid is 12 + 8 = 20.
The correct answer is C.
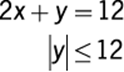
153. For how many ordered pairs (x,y) that are solutions of the system above are x and y both integers?
1. (A) 7
2. (B) 10
3. (C) 12
4. (D) 13
5. (E) 14
Algebra Absolute value
From ![]() , if y must be an integer, then y must be in the set
, if y must be an integer, then y must be in the set ![]() . Since
. Since ![]() , then
, then 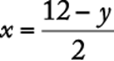 . If x must be an integer, then
. If x must be an integer, then ![]() must be divisible by 2; that is,
must be divisible by 2; that is, ![]() must be even. Since 12 is even,
must be even. Since 12 is even, ![]() is even if and only if y is even. This eliminates all odd integers from S, leaving only the even integers
is even if and only if y is even. This eliminates all odd integers from S, leaving only the even integers ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and 0. Thus, there are 13 possible integer y-values, each with a corresponding integer x-value and, therefore, there are 13 ordered pairs (x,y), where x and y are both integers, that solve the system.
, and 0. Thus, there are 13 possible integer y-values, each with a corresponding integer x-value and, therefore, there are 13 ordered pairs (x,y), where x and y are both integers, that solve the system.
The correct answer is D.
154. The points R, T, and U lie on a circle that has radius 4. If the length of arc RTU is ![]() , what is the length of line segment RU?
, what is the length of line segment RU?
1. (A) ![]()
2. (B) ![]()
3. (C) 3
4. (D) 4
5. (E) 6
Geometry Circles; Triangles; Circumference
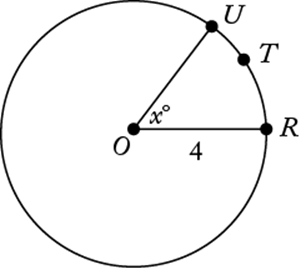
In the figure above, O is the center of the circle that contains R, T, and U and x is the degree measure of ![]() . Since the circumference of the circle is
. Since the circumference of the circle is ![]() and there are
and there are ![]() in the circle, the ratio of the length of arc RTU to the circumference of the circle is the same as the ratio of x to 360. Therefore,
in the circle, the ratio of the length of arc RTU to the circumference of the circle is the same as the ratio of x to 360. Therefore, 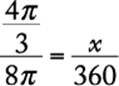 . Then
. Then 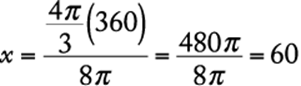 . This means that
. This means that ![]() is an isosceles triangle with side lengths
is an isosceles triangle with side lengths ![]() and vertex angle measuring
and vertex angle measuring ![]() . The base angles of
. The base angles of ![]() must have equal measures and the sum of their measures must be
must have equal measures and the sum of their measures must be ![]() . Therefore, each base angle measures
. Therefore, each base angle measures ![]() ,
, ![]() is equilateral, and
is equilateral, and ![]() .
.
The correct answer is D.
155. A certain university will select 1 of 7 candidates eligible to fill a position in the mathematics department and 2 of 10 candidates eligible to fill 2 identical positions in the computer science department. If none of the candidates is eligible for a position in both departments, how many different sets of 3 candidates are there to fill the 3 positions?
1. (A) 42
2. (B) 70
3. (C) 140
4. (D) 165
5. (E) 315
Arithmetic Elementary combinatorics
To fill the position in the math department, 1 candidate will be selected from a group of 7 eligible candidates, and so there are 7 sets of 1 candidate each to fill the position in the math department. To fill the positions in the computer science department, any one of the 10 eligible candidates can be chosen for the first position and any of the remaining 9 eligible candidates can be chosen for the second position, making a total of ![]() sets of 2 candidates to fill the computer science positions. But, this number includes the set in which Candidate A was chosen to fill the first position and Candidate B was chosen to fill the second position as well as the set in which Candidate B was chosen for the first position and Candidate A was chosen for the second position. These sets are not different essentially since the positions are identical and in both sets Candidates A and B are chosen to fill the 2 positions. Therefore, there are
sets of 2 candidates to fill the computer science positions. But, this number includes the set in which Candidate A was chosen to fill the first position and Candidate B was chosen to fill the second position as well as the set in which Candidate B was chosen for the first position and Candidate A was chosen for the second position. These sets are not different essentially since the positions are identical and in both sets Candidates A and B are chosen to fill the 2 positions. Therefore, there are  sets of 2 candidates to fill the computer science positions. Then, using the multiplication principle, there are
sets of 2 candidates to fill the computer science positions. Then, using the multiplication principle, there are ![]() different sets of 3 candidates to fill the 3 positions.
different sets of 3 candidates to fill the 3 positions.
The correct answer is E.
156. A survey of employers found that during 1993 employment costs rose 3.5 percent, where employment costs consist of salary costs and fringe-benefit costs. If salary costs rose 3 percent and fringe-benefit costs rose 5.5 percent during 1993, then fringe-benefit costs represented what percent of employment costs at the beginning of 1993?
1. (A) 16.5%
2. (B) 20%
3. (C) 35%
4. (D) 55%
5. (E) 65%
Algebra; Arithmetic First-degree equations; Percents
Let E represent employment costs, S represent salary costs, and F represent fringe-benefit costs. Then ![]() . An increase of 3 percent in salary costs and a 5.5 percent increase in fringe-benefit costs resulted in a 3.5 percent increase in employment costs. Therefore
. An increase of 3 percent in salary costs and a 5.5 percent increase in fringe-benefit costs resulted in a 3.5 percent increase in employment costs. Therefore ![]() . But,
. But, ![]() , so
, so ![]() . Combining like terms gives
. Combining like terms gives ![]() or
or ![]() . Then,
. Then, 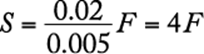 . Thus, since
. Thus, since ![]() , it follows that
, it follows that ![]() . Then, F as a percent of E is
. Then, F as a percent of E is 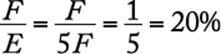 .
.
The correct answer is B.
157. The subsets of the set {w, x, y} are {w}, {x}, {y}, {w, x}, {w, y}, {x, y}, {w, x, y}, and { } (the empty subset). How many subsets of the set {w, x, y, z} contain w?
1. (A) Four
2. (B) Five
3. (C) Seven
4. (D) Eight
5. (E) Sixteen
Arithmetic Sets
As shown in the table, the subsets of {w, x, y, z} can be organized into two columns, those subsets of {w, x, y, z} that do not contain w (left column) and the corresponding subsets of {w, x, y, z} that contain w (right column), and each of these collections has the same number of sets. Therefore, there are 8 subsets of {w, x, y, z} that contain w.
|
subsets not containing w |
subsets containing w |
|
{ } |
{w} |
|
{x} |
{w, x} |
|
{y} |
{w, y} |
|
{z} |
{w, z} |
|
{x, y} |
{w, x, y} |
|
{x, z} |
{w, x, z} |
|
{y, z} |
{w, y, z} |
|
{x, y, z} |
{w, x, y, z} |
The correct answer is D.
158. There are 10 books on a shelf, of which 4 are paperbacks and 6 are hardbacks. How many possible selections of 5 books from the shelf contain at least one paperback and at least one hardback?
1. (A) 75
2. (B) 120
3. (C) 210
4. (D) 246
5. (E) 252
Arithmetic Elementary combinatorics
The number of selections of 5 books containing at least one paperback and at least one hardback is equal to T − N, where T is the total number of selections of 5 books and N is the number of selections that do not contain both a paperback and a hardback. The value of T is 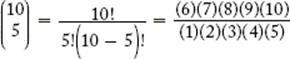 = (7)(2)(9)(2) = 252.
= (7)(2)(9)(2) = 252.
To find the value of N, first note that no selection of 5 books can contain all paperbacks, since there are only 4 paperback books. Thus, the value of N is equal to the number of selections of 5 books that contain all hardbacks, which is equal to 6 since there are 6 ways that a single hardback can be left out when choosing the 5 hardback books. It follows that the number of selections of 5 books containing at least one paperback and at least one hardback is T − N = 252 − 6 = 246.
The correct answer is D.
159. If x is to be chosen at random from the set {1, 2, 3, 4} and y is to be chosen at random from the set {5, 6, 7}, what is the probability that xy will be even?
1. (A) ![]()
2. (B) ![]()
3. (C) ![]()
4. (D) ![]()
5. (E) ![]()
Arithmetic; Algebra Probability; Concepts of sets
By the principle of multiplication, since there are 4 elements in the first set and 3 elements in the second set, there are ![]() possible products of xy, where x is chosen from the first set and y is chosen from the second set. These products will be even EXCEPT when both x and y are odd. Since there are 2 odd numbers in the first set and 2 odd numbers in the second set, there are
possible products of xy, where x is chosen from the first set and y is chosen from the second set. These products will be even EXCEPT when both x and y are odd. Since there are 2 odd numbers in the first set and 2 odd numbers in the second set, there are ![]() products of x and y that are odd. This means that the remaining
products of x and y that are odd. This means that the remaining ![]() products are even. Thus, the probability that xy is even is
products are even. Thus, the probability that xy is even is 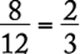 .
.
The correct answer is D.
160. The function f is defined for each positive three-digit integer n by f(n) = 2x 3y 5z, where x, y, and z are the hundreds, tens, and units digits of n, respectively. If m and v are three-digit positive integers such that f(m) = 9f(v), then m − v =
1. (A) 8
2. (B) 9
3. (C) 18
4. (D) 20
5. (E) 80
Algebra Place value
Let the hundreds, tens, and units digits of m be A, B, and C, respectively; and let the hundreds, tens, and units digits of v be a, b, and c, respectively. From f(m) = 9f(v) it follows that 2A3B5C = 9(2a3b5c) = 32(2a3b5c) = 2a3b+ 25c. Therefore, A = a, B = b + 2, and C =c. Now calculate m − v.
|
m − v = (100A + 10B + C) − (100a + 10b + c) |
place value property |
|
= (100a + 10(b + 2) + c) − (100a + 10b + c) |
obtained above |
|
= 10(b + 2) − 10b |
combine like terms |
|
= 10b + 20 − 10b |
distributive property |
|
= 20 |
combine like terms |
The correct answer is D.
161. If 1050 − 74 is written as an integer in base 10 notation, what is the sum of the digits in that integer?
1. (A) 424
2. (B) 433
3. (C) 440
4. (D) 449
5. (E) 467
Arithmetic Properties of numbers
|
102 − 74 |
= |
100 − 74 |
= |
26 |
|
103 − 74 |
= |
1,000 − 74 |
= |
926 |
|
104 − 74 |
= |
10,000 − 74 |
= |
9,926 |
|
105 − 74 |
= |
100,000 − 74 |
= |
99,926 |
|
106 − 74 |
= |
1,000,000 − 74 |
= |
999,926 |
From the table above it is clear that 1050 − 74 in base 10 notation will be 48 digits of 9 followed by the digits 2 and 6. Therefore, the sum of the digits of 1050 − 74 is equal to 48(9) + 2 + 6 = 440.
The correct answer is C.
162. A certain company that sells only cars and trucks reported that revenues from car sales in 1997 were down 11 percent from 1996 and revenues from truck sales in 1997 were up 7 percent from 1996. If total revenues from car sales and truck sales in 1997 were up 1 percent from 1996, what is the ratio of revenue from car sales in 1996 to revenue from truck sales in 1996?
1. (A) 1:2
2. (B) 4:5
3. (C) 1:1
4. (D) 3:2
5. (E) 5:3
Algebra; Arithmetic First-degree equations; Percents
Let C96 and C97 represent revenues from car sales in 1996 and 1997, respectively, and let T96 and T97 represent revenues from truck sales in 1996 and 1997, respectively. A decrease of 11 percent in revenue from car sales from 1996 to 1997 can be represented as ![]() , and a 7 percent increase in revenue from truck sales from 1996 to 1997 can be represented as
, and a 7 percent increase in revenue from truck sales from 1996 to 1997 can be represented as ![]() . An overall increase of 1 percent in revenue from car and truck sales from 1996 to 1997 can be represented as
. An overall increase of 1 percent in revenue from car and truck sales from 1996 to 1997 can be represented as ![]() . Then, by substitution of expressions for C97 and T97 that were derived above,
. Then, by substitution of expressions for C97 and T97 that were derived above, ![]() and so
and so ![]()
![]()
![]() . Then, combining like terms gives
. Then, combining like terms gives ![]() or
or ![]() . Thus
. Thus 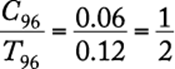 . The ratio of revenue from car sales in 1996 to revenue from truck sales in 1996 is 1:2.
. The ratio of revenue from car sales in 1996 to revenue from truck sales in 1996 is 1:2.
The correct answer is A.
163. 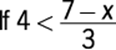 , which of the following must be true?
, which of the following must be true?
I. ![]()
II. ![]()
III. ![]() is positive.
is positive.
1. (A) II only
2. (B) III only
3. (C) I and II only
4. (D) II and III only
5. (E) I, II, and III
Algebra Inequalities
Given that 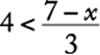 , it follows that
, it follows that ![]() . Then,
. Then, ![]() or, equivalently,
or, equivalently, ![]() .
.
6. I. If 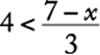 , then
, then ![]() . If
. If ![]() were true then, by combining
were true then, by combining ![]() and
and ![]() , it would follow that
, it would follow that ![]() , which cannot be true. Therefore, it is not the case that, if
, which cannot be true. Therefore, it is not the case that, if 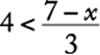 , then Statement I must be true. In fact, Statement I is never true.
, then Statement I must be true. In fact, Statement I is never true.
7. II. If 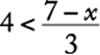 , then
, then ![]() , and it follows that
, and it follows that ![]() . Since
. Since ![]() , then
, then ![]() and
and ![]() . If
. If ![]() , then
, then ![]() and by substitution,
and by substitution, ![]() . Therefore, Statement II must be true for every value of x such that
. Therefore, Statement II must be true for every value of x such that ![]() . Therefore, Statement II must be true if
. Therefore, Statement II must be true if 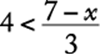 .
.
8. III. If 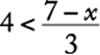 , then
, then ![]() and
and ![]() . But, if
. But, if ![]() , then it follows that
, then it follows that ![]() and so
and so ![]() is positive. Therefore Statement III must be true if
is positive. Therefore Statement III must be true if 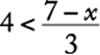 .
.
The correct answer is D.
164. A certain right triangle has sides of length x, y, and z, where ![]() . If the area of this triangular region is 1, which of the following indicates all of the possible values of y?
. If the area of this triangular region is 1, which of the following indicates all of the possible values of y?
1. (A) ![]()
2. (B) 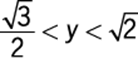
3. (C) 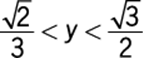
4. (D) 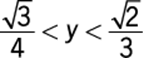
5. (E) 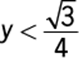
Geometry; Algebra Triangles; Area; Inequalities
Since x, y, and z are the side lengths of a right triangle and ![]() , it follows that x and y are the lengths of the legs of the triangle and so the area of the triangle is
, it follows that x and y are the lengths of the legs of the triangle and so the area of the triangle is ![]() . But, it is given that the area is 1 and so
. But, it is given that the area is 1 and so 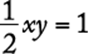 . Then,
. Then, ![]() and
and 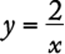 . Under the assumption that x, y, and z are all positive since they are the side lengths of a triangle,
. Under the assumption that x, y, and z are all positive since they are the side lengths of a triangle, ![]() implies
implies 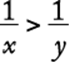 and then
and then 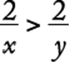 . But,
. But, 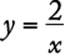 , so by substitution,
, so by substitution, 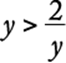 , which implies that
, which implies that ![]() since y is positive. Thus,
since y is positive. Thus, ![]() .
.
Alternatively, if ![]() and
and ![]() , then
, then ![]() . If
. If ![]() and
and ![]() , then
, then ![]() . But,
. But, ![]() so one of x or y must be less than
so one of x or y must be less than ![]() and the other must be greater than
and the other must be greater than ![]() . Since
. Since ![]() , it follows that
, it follows that ![]() and
and ![]() .
.
The correct answer is A.
165. A set of numbers has the property that for any number t in the set, ![]() is in the set. If −1 is in the set, which of the following must also be in the set?
is in the set. If −1 is in the set, which of the following must also be in the set?
I. −3
II. 1
III. 5
1. (A) I only
2. (B) II only
3. (C) I and II only
4. (D) II and III only
5. (E) I, II, and III
Arithmetic Properties of numbers
It is given that −1 is in the set and, if t is in the set, then ![]() is in the set.
is in the set.
6. I. Since {−1, 1, 3, 5, 7, 9, 11, . . .} contains −1 and satisfies the property that if t is in the set, then ![]() is in the set, it is not true that −3 must be in the set.
is in the set, it is not true that −3 must be in the set.
7. II. Since −1 is in the set, ![]() is in the set. Therefore, it must be true that 1 is in the set.
is in the set. Therefore, it must be true that 1 is in the set.
8. III. Since −1 is in the set, ![]() is in the set. Since 1 is in the set,
is in the set. Since 1 is in the set, ![]() is in the set. Since 3 is in the set,
is in the set. Since 3 is in the set, ![]() is in the set. Therefore, it must be true that 5 is in the set.
is in the set. Therefore, it must be true that 5 is in the set.
The correct answer is D.
166. A couple decides to have 4 children. If they succeed in having 4 children and each child is equally likely to be a boy or a girl, what is the probability that they will have exactly 2 girls and 2 boys?
1. (A) ![]()
2. (B) ![]()
3. (C) ![]()
4. (D) ![]()
5. (E) ![]()
Arithmetic Probability
Representing the birth order of the 4 children as a sequence of 4 letters, each of which is B for boy and G for girl, there are 2 possibilities (B or G) for the first letter, 2 for the second letter, 2 for the third letter, and 2 for the fourth letter, making a total of ![]() sequences. The table below categorizes some of these 16 sequences.
sequences. The table below categorizes some of these 16 sequences.
|
# of boys |
# of girls |
Sequences |
# of sequences |
|
0 |
4 |
GGGG |
1 |
|
1 |
3 |
BGGG, GBGG, GGBG, GGGB |
4 |
|
3 |
1 |
GBBB, BGBB, BBGB, BBBG |
4 |
|
4 |
0 |
BBBB |
1 |
The table accounts for ![]() sequences. The other 6 sequences will have 2Bs and 2Gs. Therefore the probability that the couple will have exactly 2 boys and 2 girls is
sequences. The other 6 sequences will have 2Bs and 2Gs. Therefore the probability that the couple will have exactly 2 boys and 2 girls is  .
.
For the mathematically inclined, if it is assumed that a couple has a fixed number of children, that the probability of having a girl each time is p, and that the sex of each child is independent of the sex of the other children, then the number of girls, x, born to a couple with n children is a random variable having the binomial probability distribution. The probability of having exactly x girls born to a couple with n children is given by the formula  . For the problem at hand, it is given that each child is equally likely to be a boy or a girl, and so
. For the problem at hand, it is given that each child is equally likely to be a boy or a girl, and so 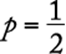 . Thus, the probability of having exactly 2 girls born to a couple with 4 children is
. Thus, the probability of having exactly 2 girls born to a couple with 4 children is 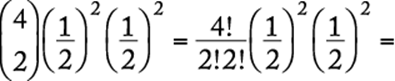
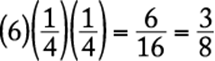 .
.
The correct answer is A.
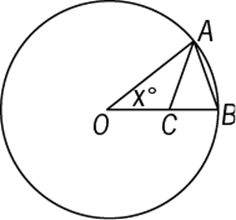
167. In the figure above, point O is the center of the circle and ![]() . What is the value of x?
. What is the value of x?
1. (A) 40
2. (B) 36
3. (C) 34
4. (D) 32
5. (E) 30
Geometry Angles
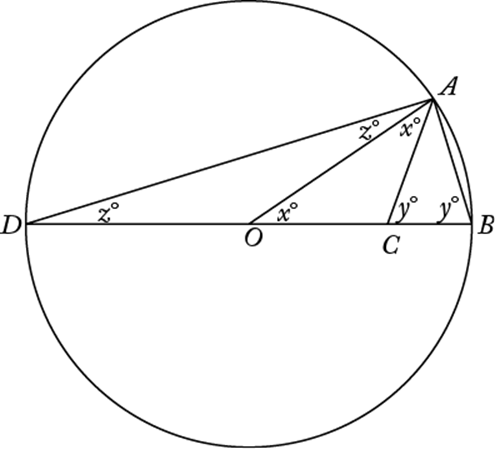
Consider the figure above, where ![]() is a diameter of the circle with center O and
is a diameter of the circle with center O and ![]() is a chord. Since
is a chord. Since ![]() ,
, ![]() is isosceles and so the base angles,
is isosceles and so the base angles, ![]() and
and ![]() , have the same degree measure. The measure of
, have the same degree measure. The measure of ![]() is given as
is given as ![]() , so the measure of
, so the measure of ![]() is
is ![]() . Since
. Since ![]() ,
, ![]() is isosceles and so the base angles,
is isosceles and so the base angles, ![]() and
and ![]() , have the same degree measure. The measure of each is marked as
, have the same degree measure. The measure of each is marked as ![]() . Likewise, since
. Likewise, since ![]() and
and ![]() are radii of the circle,
are radii of the circle, ![]() , and
, and ![]() is isosceles with base angles,
is isosceles with base angles, ![]() and
and ![]() , each measuring
, each measuring ![]() . Each of the following statements is true:
. Each of the following statements is true:
6. (i) The measure of ![]() is
is ![]() since the sum of the measures of the angles of
since the sum of the measures of the angles of ![]() is 180.
is 180.
7. (ii) ![]() is a right angle (because
is a right angle (because ![]() is a diameter of the circle) and so
is a diameter of the circle) and so ![]() , or, equivalently,
, or, equivalently, ![]() .
.
8. (iii) ![]() since the sum of the measures of the angles of right triangle
since the sum of the measures of the angles of right triangle ![]() is 180, or, equivalently,
is 180, or, equivalently, ![]() .
.
9. (iv) ![]() because the measure of exterior angle
because the measure of exterior angle ![]() to
to ![]() is the sum of the measures of the two opposite interior angles,
is the sum of the measures of the two opposite interior angles, ![]() and
and ![]() .
.
10.(v) ![]() because the measure of exterior angle
because the measure of exterior angle ![]() to
to ![]() is the sum of the measures of the two opposite interior angles,
is the sum of the measures of the two opposite interior angles, ![]() and
and ![]() .
.
Multiplying the final equation in (iii) by 2 gives ![]() . But,
. But, ![]() in (iv), so
in (iv), so ![]() . Finally, the sum of the measures of the angles of
. Finally, the sum of the measures of the angles of ![]() is 180 and so
is 180 and so ![]() . Then from (v),
. Then from (v), ![]() ,
, ![]() , and
, and ![]() .
.
The correct answer is B.
168. When 10 is divided by the positive integer n, the remainder is ![]() . Which of the following could be the value of n?
. Which of the following could be the value of n?
1. (A) 3
2. (B) 4
3. (C) 7
4. (D) 8
5. (E) 12
Algebra Properties of numbers
If q is the quotient and ![]() is the remainder when 10 is divided by the positive integer n, then
is the remainder when 10 is divided by the positive integer n, then ![]() . So,
. So, ![]() . This means that n must be a factor of 14 and so
. This means that n must be a factor of 14 and so ![]() ,
, ![]() ,
, ![]() , or
, or ![]() since n is a positive integer and the only positive integer factors of 14 are 1, 2, 7, and 14. The only positive integer factor of 14 given in the answer choices is 7.
since n is a positive integer and the only positive integer factors of 14 are 1, 2, 7, and 14. The only positive integer factor of 14 given in the answer choices is 7.
The correct answer is C.
169. An airline passenger is planning a trip that involves three connecting flights that leave from Airports A, B, and C, respectively. The first flight leaves Airport A every hour, beginning at 8:00 a.m., and arrives at Airport B ![]() hours later. The second flight leaves Airport B every 20 minutes, beginning at 8:00 a.m., and arrives at Airport C
hours later. The second flight leaves Airport B every 20 minutes, beginning at 8:00 a.m., and arrives at Airport C ![]() hours later. The third flight leaves Airport C every hour, beginning at 8:45 a.m. What is the least total amount of time the passenger must spend between flights if all flights keep to their schedules?
hours later. The third flight leaves Airport C every hour, beginning at 8:45 a.m. What is the least total amount of time the passenger must spend between flights if all flights keep to their schedules?
1. (A) 25 min
2. (B) 1 hr 5 min
3. (C) 1 hr 15 min
4. (D) 2 hr 20 min
5. (E) 3 hr 40 min
Arithmetic Operations on rational numbers
Since the flight schedules at each of Airports A, B, and C are the same hour after hour, assume that the passenger leaves Airport A at 8:00 and arrives at Airport B at 10:30. Since flights from Airport B leave at 20-minute intervals beginning on the hour, the passenger must wait 10 minutes at Airport B for the flight that leaves at 10:40 and arrives at Airport C ![]() hours or 1 hour 10 minutes later. Thus, the passenger arrives at Airport C at 11:50. Having arrived too late for the 11:45 flight from Airport C, the passenger must wait 55 minutes for the 12:45 flight. Thus, the least total amount of time the passenger must spend waiting between flights is
hours or 1 hour 10 minutes later. Thus, the passenger arrives at Airport C at 11:50. Having arrived too late for the 11:45 flight from Airport C, the passenger must wait 55 minutes for the 12:45 flight. Thus, the least total amount of time the passenger must spend waiting between flights is ![]() minutes, or 1 hour 5 minutes.
minutes, or 1 hour 5 minutes.
The correct answer is B.
170. If n is a positive integer and n2 is divisible by 72, then the largest positive integer that must divide n is
1. (A) 6
2. (B) 12
3. (C) 24
4. (D) 36
5. (E) 48
Arithmetic Properties of numbers
Since n2 is divisible by 72, ![]() for some positive integer k. Since
for some positive integer k. Since ![]() , then 72k must be a perfect square. Since
, then 72k must be a perfect square. Since ![]() , then
, then ![]() for some positive integer m in order for 72k to be a perfect square. Then,
for some positive integer m in order for 72k to be a perfect square. Then, ![]()
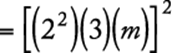 , and
, and ![]() . The positive integers that MUST divide n are 1, 2, 3, 4, 6, and 12. Therefore, the largest positive integer that must divide n is 12.
. The positive integers that MUST divide n are 1, 2, 3, 4, 6, and 12. Therefore, the largest positive integer that must divide n is 12.
The correct answer is B.
171. If n is a positive integer and ![]() , which of the following could NOT be a value of k?
, which of the following could NOT be a value of k?
1. (A) 1
2. (B) 4
3. (C) 7
4. (D) 25
5. (E) 79
Arithmetic Operations on rational numbers
For a number to equal 3n, the number must be a power of 3. Substitute the answer choices for k in the equation given, and determine which one does not yield a power of 3.
|
A |
|
power of 3 (31) |
|
B |
|
multiple of 3, but NOT a power of 3 |
|
C |
|
power of 3 (32) |
|
D |
|
power of 3 (33) |
|
E |
|
power of 3 (34) |
The correct answer is B.
172. A certain grocery purchased x pounds of produce for p dollars per pound. If y pounds of the produce had to be discarded due to spoilage and the grocery sold the rest for s dollars per pound, which of the following represents the gross profit on the sale of the produce?
1. (A) ![]()
2. (B) ![]()
3. (C) ![]()
4. (D) ![]()
5. (E) ![]()
Algebra Simplifying algebraic expressions; Applied problems
Since the grocery bought x pounds of produce for p dollars per pound, the total cost of the produce was xp dollars. Since y pounds of the produce was discarded, the grocery sold ![]() pounds of produce at the price of s dollars per pound, yielding a total revenue of
pounds of produce at the price of s dollars per pound, yielding a total revenue of ![]() dollars. Then, the grocery”s gross profit on the sale of the produce is its total revenue minus its total cost or
dollars. Then, the grocery”s gross profit on the sale of the produce is its total revenue minus its total cost or ![]() dollars.
dollars.
The correct answer is A.
173. If x, y, and z are positive integers such that x is a factor of y, and x is a multiple of z, which of the following is NOT necessarily an integer?
1. (A) ![]()
2. (B) ![]()
3. (C) ![]()
4. (D) ![]()
5. (E) ![]()
Arithmetic Properties of numbers
Since the positive integer x is a factor of y, then ![]() for some positive integer k. Since x is a multiple of the positive integer z, then
for some positive integer k. Since x is a multiple of the positive integer z, then ![]() for some positive integer m.
for some positive integer m.
Substitute these expressions for x and/or y into each answer choice to find the one expression that is NOT necessarily an integer.
6. A 
![]() , which MUST be an integer
, which MUST be an integer
7. B  , which NEED NOT be an integer
, which NEED NOT be an integer
Because only one of the five expressions need not be an integer, the expressions given in C, D, and E need not be tested. However, for completeness,
8. C 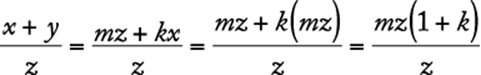
![]() , which MUST be an integer
, which MUST be an integer
9. D 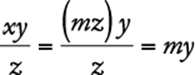 , which MUST be an integer
, which MUST be an integer
10.E 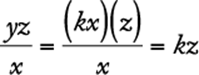 , which MUST be an integer
, which MUST be an integer
The correct answer is B.
174. Running at their respective constant rates, Machine X takes 2 days longer to produce w widgets than Machine Y. At these rates, if the two machines together produce ![]() widgets in 3 days, how many days would it take Machine X alone to produce 2w widgets?
widgets in 3 days, how many days would it take Machine X alone to produce 2w widgets?
1. (A) 4
2. (B) 6
3. (C) 8
4. (D) 10
5. (E) 12
Algebra; Applied problems
If x, where ![]() , represents the number of days Machine X takes to produce w widgets, then Machine Y takes
, represents the number of days Machine X takes to produce w widgets, then Machine Y takes ![]() days to produce w widgets. It follows that Machines X and Y can produce
days to produce w widgets. It follows that Machines X and Y can produce ![]() and
and ![]() widgets, respectively, in 1 day and together they can produce
widgets, respectively, in 1 day and together they can produce ![]() widgets in 1 day. Since it is given that, together, they can produce
widgets in 1 day. Since it is given that, together, they can produce ![]() widgets in 3 days, it follows that, together, they can produce
widgets in 3 days, it follows that, together, they can produce 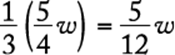 widgets in 1 day. Thus,
widgets in 1 day. Thus,
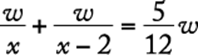
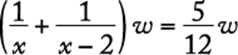
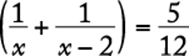
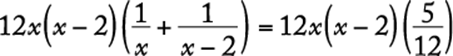
![]()
![]()
![]()
![]()
![]()
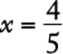 or 6
or 6
Therefore, since ![]() , it follows that
, it follows that ![]() . Machine X takes 6 days to produce w widgets and
. Machine X takes 6 days to produce w widgets and ![]() days to produce 2w widgets.
days to produce 2w widgets.
The correct answer is E.
175. A square wooden plaque has a square brass inlay in the center, leaving a wooden strip of uniform width around the brass square. If the ratio of the brass area to the wooden area is 25 to 39, which of the following could be the width, in inches, of the wooden strip?
1. I. 1
2. II. 3
3. III. 4
4. (A) I only
5. (B) II only
6. (C) I and II only
7. (D) I and III only
8. (E) I, II, and III
Geometry Area
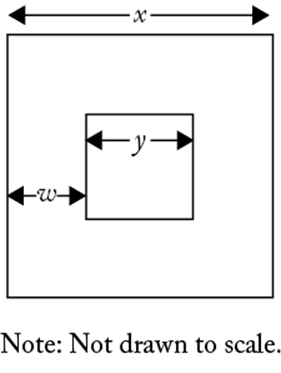
Let x represent the side length of the entire plaque, let y represent the side length of the brass inlay, and w represent the uniform width of the wooden strip around the brass inlay, as shown in the figure above. Since the ratio of the area of the brass inlay to the area of the wooden strip is 25 to 39, the ratio of the area of the brass inlay to the area of the entire plaque is 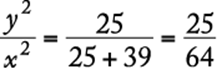 . Then,
. Then, 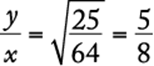 and
and 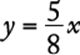 . Also,
. Also, ![]() and
and 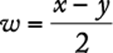 . Substituting
. Substituting ![]() for y into this expression for wgives
for y into this expression for wgives 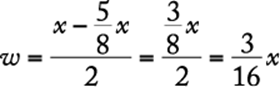 . Thus,
. Thus,
9. I. If the plaque were ![]() inches on a side, then the width of the wooden strip would be 1 inch, and so 1 inch is a possible width for the wooden strip.
inches on a side, then the width of the wooden strip would be 1 inch, and so 1 inch is a possible width for the wooden strip.
10.II. If the plaque were 16 inches on a side, then the width of the wooden strip would be 3 inches, and so 3 inches is a possible width for the wooden strip.
11.III. If the plaque were ![]() inches on a side, then the width of the wooden strip would be 4 inches, and so 4 inches is a possible width for the wooden strip.
inches on a side, then the width of the wooden strip would be 4 inches, and so 4 inches is a possible width for the wooden strip.
The correct answer is E.
176. 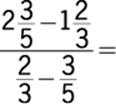
1. (A) 16
2. (B) 14
3. (C) 3
4. (D) 1
5. (E) −1
Arithmetic Operations on rational numbers
Work the problem:
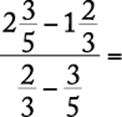
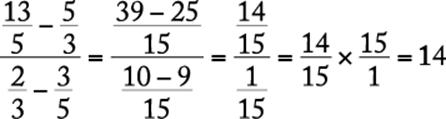
The correct answer is B.