Math Workout for the GRE, 3rd Edition (2013)

Chapter 8. The Rest of the Story

TYING UP LOOSE ENDS

So here it is, the last chapter about quantitative topics on the GRE. Most of the material we review in this chapter will probably appear less frequently on the GRE, and most of it deals with data analysis. There are a lot of formulas in this chapter that you’d do well to memorize, because it will save you a considerable amount of time when you sit down to take the test. Let’s begin.

FUNCTIONS

Sometimes the GRE will make up a mathematical operator. You will see some weird shape, which you’ve never seen in a math problem, and be asked to solve a problem using this weird shape. This is simply the GRE trying to confuse you.

These questions are asking about functions. A function is simply a set of directions. For instance, think of the word “chop” in a recipe. The word chop is actually telling you to do many things: take out a cutting board, rinse the vegetable or fruit to be chopped, take out a knife, place the vegetable on the cutting board, et cetera et cetera. If a recipe says “Chop 3 carrots,” then you must do all those things that chopping entails, but using carrots. If the recipe says “Chop 2 stalks of celery,” then you must do all of those chopping things, but with celery.

A function is the same way. It is a set of rules, and the GRE will ask you to perform those rules on a certain number. If the GRE invents some function, for instance that ♦x = 4x + 2, and then asks what ♦5 is, then figure out what rules you need to follow. Our original function was ♦x, but notice how with ♦5, we replaced the x that was after the ♦ with a 5? Well, let’s do the same thing with the equation we’re given for ♦x: Replace each x with a 5. We then get that ♦5 = 4(5) + 2 = 20 + 2 = 22.

Let’s try a practice problem. Look for what numbers we’ll need to place in our original function, and where each number will go.

Question 10 of 20

If x∼y is defined as the sum of all of the prime integers between x and y, which of the following is equal to 17 ?

Indicate all such values.

1∼10

4∼10

6∼12

14∼18

Here’s How to Crack It

Here we have a completely made-up mathematical operator. This question says that whenever you see a ∼, you must find the sum of all the prime integers between those two numbers. Rather than write out all the primes and figure out which numbers we could pick to get 17, let’s PITA. As we Plug In each answer choice, we’re going to have to find the sum of all the prime integers between those two numbers. So 1∼10 is the sum of all the prime integers between 1 and 10, which is 2 + 3 + 5 + 7 = 17, so (A) is an answer. 4∼10 = 5 + 7 = 12, so cross off (B). 6∼12 = 7 + 11 = 18, so cross off (C). For the last answer, the only prime integer between 14 and 18 is 17, and since the sum of 17 and nothing is 17, (D) is also an answer. The answers are therefore (A) and (D).

You may also see function questions of the form f(x) = x² + 5. In that case, if they ask for f(3), then wherever there used to be an x in our original function, we’ll put a 3: f(3) = 3² + 5 = 9 + 5 = 14.

Whenever you see something unfamiliar on a GRE question, look to see if the question itself tells you what to do, and follow those directions.

FACTORIALS!

The term n! is referred to as “n factorial,” and whenever a factorial shows up on the GRE it pertains to the number of ways a number of elements can be chosen, or arranged. We’ll discuss this further when we get to the section on permutations and combinations, a little later. But for now:

The term n! (read as “n factorial”) represents the product of all integers from n to 1, inclusive. For example, 5! = 5 × 4 × 3 × 2 × 1, or 120.

Factorial questions can look like they require more work than they really do. This is because you can usually cancel a lot of numbers and make a huge sequence of multiplications into something much more manageable. Here’s an example:

Question 16 of 20

Quantity A is greater.

Quantity B is greater.

The two quantities are equal.

The relationship cannot be determined from the information given.

Trigger: Factorials
with division.

Response: Expand
factorial and reduce.

Here’s How to Crack It

When evaluating Quantity A, it might look like you’re about to spend 10 minutes multiplying all those numbers on your calculator. Break the fraction down first, though, and you’ll see that all but one of the numbers cancels out.

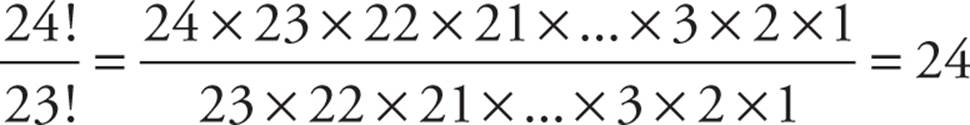
As you can see, you can cancel out everything from the 23 on, and you’re left with 24. Quantity B also equals 24 (4 × 3 × 2 × 1), so the answer is (C).

Sometimes, however, a GRE question will involve adding or subtracting factorials. In that case, we’re going to have to factor.

Question 10 of 20

What is the value of the expression ?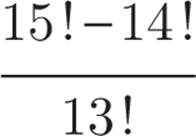

Trigger: Factorials with
addition or subtraction.

Response: Factor out
common factorials.

Here’s How to Crack It

15! is too large to enter into the calculator, so we’re going to have to factor out what 15! and 14! have in common. Since 15! is the same as 15 × 14 × 13 × 12 × 11 × 10 … and 14! is 14 × 13 × 12 × 11 …, we can rewrite 15! as 15(14!). Both 15(14!) and 14! contain 14!, so we can rewrite the fraction as 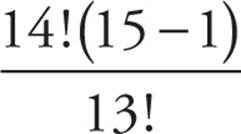. Note that if we distributed the 14! to each term within the parentheses, we’d have back our original numerator: 15! − 14! We can simplify the 15 − 1 inside the parentheses, giving us 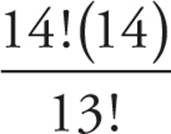. Now it’s time to cancel out the two factorials, as we did with Question 16. 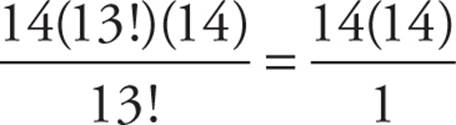= 196.

Factorials Quick Quiz

Question 1 of 4

=

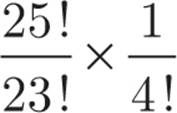Question 2 of 4

Each of the following is equivalent to 6! EXCEPT

3! × 5!

4! × 30

6² × 20

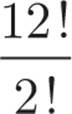
Question 3 of 4

Quantity A is greater.

Quantity B is greater.

The two quantities are equal.

The relationship cannot be determined from the information given.

Question 4 of 4

=

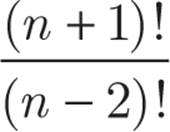0

n!

n³ − n

n³ − 4n

(2n)!

Explanations for Factorials and Arrangements Quick Quiz

1. The first term, 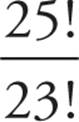, is equivalent to 25 × 24, and the second term equals 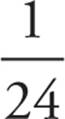. Therefore, the final term is 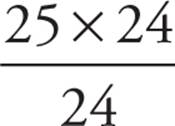, or 25.

2. All of the answer choices are equivalent to 6!, or 720, except (E), because 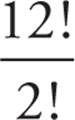is the same as 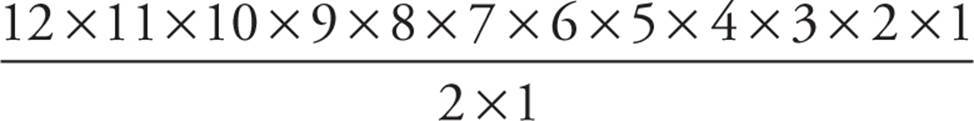. Because 12 × 11 × 10 is already 1,320, it’s possible to see that this is far bigger than 720 without even bothering with your calculator. The answer is (E).

3. Since there are no variables in this question, we can eliminate answer (D). We’ve got factorials combined with subtraction, which means we’re going to have to factor. 17! is the same as 17 × 16 × 15 × 14!. We can therefore rewrite Quantity A as 17 × 16 × 15 × 14! − 14!. Since we have 14! in both terms, we can factor out 14!, giving us 14! (17 × 16 × 15 − 1). Now it’s time for a bit of calculator work, which gives us 14!(4,080 − 1) = 14!(4,079). Both quantities have 14!, so let’s focus on the other parts. Since 4,079 is larger than 4,078, 14!(4,079) is larger than 4,078 × 14!, and the answer is (A).

4. Rather than mess with the algebra here, just Plug In a value of n (and make sure it’s greater than 2). If n = 5, then 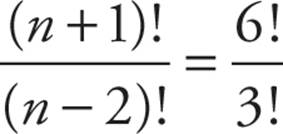, or 120 (target answer). When you plug 5 into the answer choices, n³ − n = 5³ − 5 = 125 − 5, or 120. The answer is (C).

PROBABILITY

In probability questions, something that you want to happen is a “favorable outcome,” and all of the things that could happen are “possible outcomes.” So for these types of questions, your job is to figure out the chance that a favorable outcome—an outcome you want to happen—will occur.

The probability of a favorable outcome is found by dividing the number of possible favorable outcomes by the total number of possible outcomes.

· If a favorable outcome is impossible, then the probability that it will happen is 0.

· If a favorable outcome is a certainty, then the probability that it will happen is 1.

· The probability that something will happen plus the probability that it will not happen is equal to 1.

· If more than two outcomes are possible, the sum of the probabilities of all outcomes is equal to 1.

Trigger: The word
“probability.”

Response: For each
event, find the number
of outcomes you want to
happen, and divide by
the total number of
outcomes.

Question 19 of 20

Quantity A is greater.

Quantity B is greater.

The two quantities are equal.

The relationship cannot be determined from the information given.

Here’s How to Crack It

There is only 1 jack of diamonds in a deck of 52 cards, so the probability of selecting it is 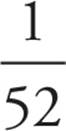. Rhode Island is only 1 of 50 American states, so the probability that it will be selected at random is 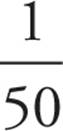. Because the denominator in Quantity A is greater, the fraction must be smaller. Therefore, the answer is (B).

Multiple Probabilities

If you’re asked to find the probability that two specific events will occur one after the other, first find the individual probabilities that each event will occur, and then multiply them. There are two different scenarios on problems like these; sometimes the odds of an individual event are different from another event, and sometimes they aren’t.

Probability of A and B = Probability of A × Probability of B

For example, if a problem involves flipping a coin, the probability that it will come up heads will always be . It will never change, because there will always be heads on one side of the coin and tails on the other. Let’s go through a typical problem you might see on the GRE.

Question 13 of 20

If a six-sided die with faces numbered one through six is rolled three times, what is the probability that 5 faces upward for all three rolls?

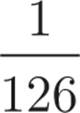
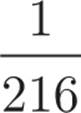
Here’s How to Crack It

There is only one 5 on the six-sided die, so the chance of rolling a 5 is . When you roll the die a second or third time, you still have a chance of rolling a 5, so the chance remains . Therefore, the chance of rolling three 5’s in a row is 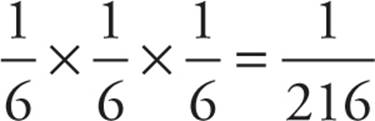The answer is (E).

Removing Items Changes the Probability

So far, our total, the denominator of our fraction, has always stayed constant. However, there will be some questions in which we remove items as we go. These problems often contain the phrase without replacement, because items are taken without replacing them. In that case, the total will change. At each point, we’ll figure out the next probability by assuming that what the problem wants to happen has happened.

For instance, imagine there are 3 red marbles and 1 green marble in a bag. What’s the probability of selecting 2 red marbles in a row? When we first reach into the bag, we’ll have a chance of pulling out a red marble: There are 3 red marbles, out of a total of 4 marbles. But what about when we reach in again? We’ll have to assume that we pulled out that first red marble. (Otherwise, who cares if we pull out a second red marble? We wanted two red marbles in a row, not a something else and then a red marble.) That means we have only 2 red marbles left, out of a total of 3 marbles, and our chance to pull that second red marble is . Now we can combine our two probabilities by multiplying them together: .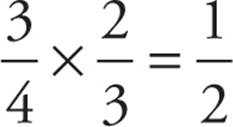

Let’s try a harder problem that uses a changing total.

Question 15 of 20

A shopping bag contains 5 green peppers and 4 red peppers. A grocer removes three of the peppers from the bag at random.

Quantity A is greater.

Quantity B is greater.

The two quantities are equal.

The relationship cannot be determined from the information given.

Here’s How to Crack It

This question is different because multiple peppers are removed, so the odds change after each pepper leaves the bag. Work with Quantity A first: When the grocer reaches in the first time, he has a chance of selecting a green pepper. The second time, there are only 4 green peppers out of a total of 8, so the chance of getting a second green pepper is . The third time, there are only 7 peppers left and 4 of them are red. The chance of getting a red is , and the composite probability is .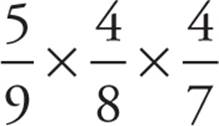

Before you multiply, look at Quantity B. The probabilities are (green), (first red), and (second red), so the composite probability is 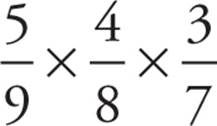. When comparing the two quantities, the denominators are the same but the numerator in Quantity B is smaller. Therefore, Quantity B itself must be smaller, and the answer must be (A).

At Least Probabilities

Some questions will not ask for the probability of a single event, but instead ask for the probability that “at least” a certain number of events will happen. For instance, let’s go back to the bag of marbles. Say there are 4 red marbles and 5 green marbles, and you’re asked the likelihood of reaching in, taking out 3 marbles, and getting at least 1 red marble.

We could find that out by figuring out the probability of getting 1 red marble and then 2 green marbles, and adding that to the probability of getting a green, a red, and a green, plus the probability of getting a green, a green, and a red. But we could get more than just one red, right? We’d also have to find the chance of RRG, RGR, and GRR, and then the probability of getting RRR, and add all of those different ways of getting at least one red marble together.

But there’s an easier way. Think of it this way: If there’s a 30% chance of rain, what’s the chance it won’t rain? 70%. Since any two mutually exclusive probabilities always add up to 100%, we can sometimes find the probability that something won’t happen rather than find the probability it will happen. Once we do, we’ll subtract it from 1, because 100% = 1.

Going back to our marble example, if you were asked “Did you pull at least 1 red marble from the bag?” and you answered “No,” then what marbles did you pull? If you didn’t pull at least 1 red marble, then you pulled all green marbles. The probability of pulling all green marbles is 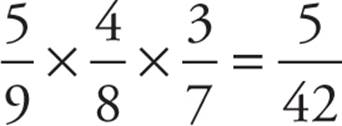. But we don’t want to pull all green marbles; we want the opposite of that. Therefore the probability of getting at least one red marble is .

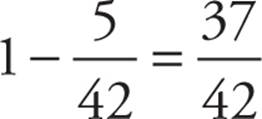Trigger: Probability
question asks “at least.”

Response: Find the
probability event won’t
happen, and subtract
from 1.

Probability Quick Quiz

Question 1 of 5

Of the 50 U.S. states, 23 border a major body of salt water.

Quantity A is greater.

Quantity B is greater.

The two quantities are equal.

The relationship cannot be determined from the information given.

Question 2 of 5

If the letters A, R, S, and T are arranged in a row, what is the probability that a proper English word is formed?

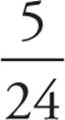
Question 3 of 5

Fred has three dimes, two nickels, and four quarters in his pocket. If he selects two coins, at random and without replacement, what is the probability that he selects two dimes?

Question 4 of 5

Harry throws two fair, six-sided dice both with faces numbered one through six..

Quantity A is greater.

Quantity B is greater.

The two quantities are equal.

The relationship cannot be determined from the information given.

Question 5 of 5

The probability of event J occuring is 0.63 while the probability that both events J and K occur is 0.42. What is the probability that event K will occur?

Give your answer as a fraction.

Explanations for Probability Quick Quiz

1. There are 50 different states; these are the possible outcomes. There are 23 states with a saltwater border, and these are the desired outcomes for Quantity A. Therefore, the probability that a randomly selected state will have a saltwater border is 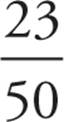. If 23 have saltwater borders, then 27 states do not. This is the desired outcome for Quantity B. The number of possible outcomes remains the same, so the probability for Quantity B is 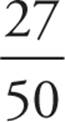. This fraction is larger, so the answer is (B).

2. There are 24 (or 4!) ways to arrange the four letters, and of these 5 form proper English words (arts, rats, star, tars, and tsar). The probability is 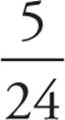. The answer is (C).

3. There are 9 coins in Fred’s pocket, 3 of which are dimes, so the probability that he will get a dime the first time is . The second time, there are only 2 dimes out of 8 coins, so the probability drops to . The composite probability is 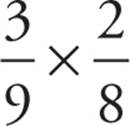, or 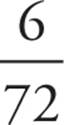. This reduces to , so the answer is (A).

4. When two fair, six-sided dice are thrown, there are 36 possible rolls. Of these, 5 will sum to 8 (2 and 6, 3 and 5, 4 and 4, 5 and 3, and 6 and 2) and 6 will sum to 7 (1 and 6, 2 and 5, 3 and 4, 4 and 3, 5 and 2, and 6 and 1). Because there are more ways to roll 7, Quantity B is greater and the answer is (B).

5. Remember that the probability of two events happening is probability of A × probability of B. Since we know that probability of J × probability of K = 0.42, and we know the probability of J is 0.63, we know that 0.63 × probability of K = 0.42. Dividing both sides by 0.63 gives us that the probability of K = .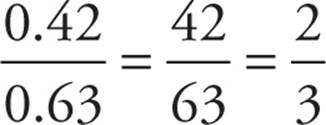

As we near the homestretch, here are two more topics that could appear on the GRE. These topics occur very rarely, and when they do appear you’ll see at most one question about them per section. Therefore, it pays to reference them here, at the end of the chapter.

GROUPS

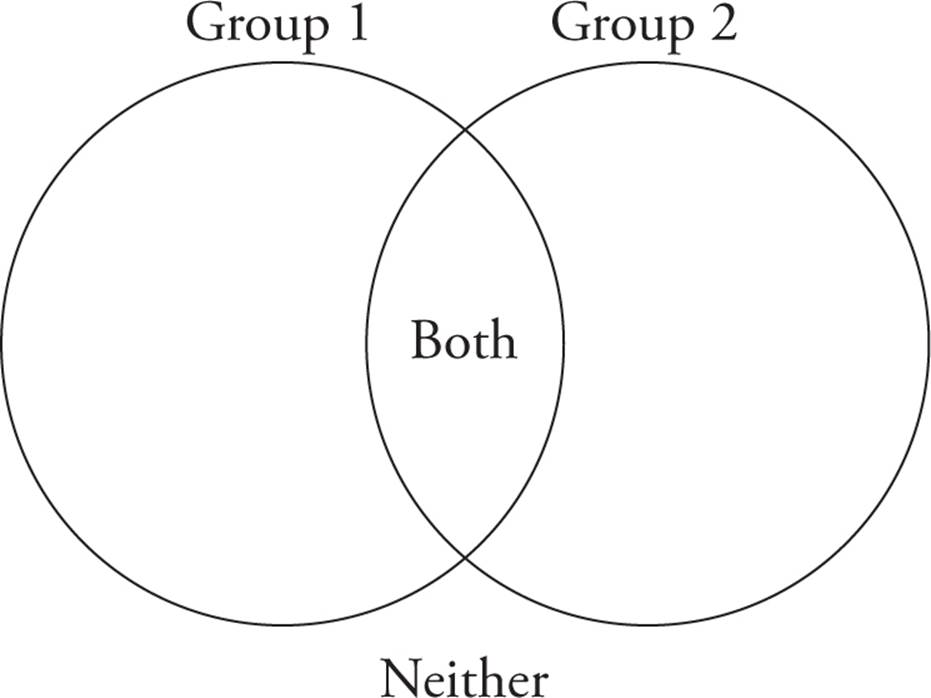
There are two basic types of group questions: those that involve overlap between two groups, and those that involve groups in which there is no overlap. The group questions with overlap can be represented visually using the classic Venn diagram below, but you may find it easier, and more straightforward, to use an equation.

Group Formula:
Total = [Group 1] + [Group 2] − [Both] + [Neither]

The first thing you’ll have to do with this sort of question is to recognize that you need to use the Group Formula. What are your clues? If there are any elements that overlap between two of the groups, then we will need to use the Group Formula. We may not have any elements that are in neither group (Neither = 0), but if we have any overlapping elements, then those elements are being counted twice: Once because they belong to Group 1, and again because they belong to Group 2. To eliminate one of the times those Both elements are being counted, we subtract the Both. Note that Group 1 includes everything in Group 1, including those that are in Both. The same applies to Group 2.

Trigger: Group problem
with overlap.

Response: Write down
Group Formula.

Let’s try a problem using the Group Formula:

Question 8 of 20

Of the 213 people who responded to a genealogical poll, 82 said they have French ancestors and 113 said they have Italian ancestors. If 51 of the respondents said they have neither French nor Italian heritage, how many have both?

33

52

69

101

124

Here’s How to Crack It

Assign the groups (Group 1 is French, Group 2 is Italian), and plug the numbers you know into the formula: 82 + 113 − B + 51 = 213. Because 246 − B = 213, B must equal 33. The answer is (A).

Either/Or Group Problems

The Group Formula is great, but it only works on problems in which there is some overlap between two groups. The GRE will also sometimes ask group questions in which there is no overlap between groups. These questions involve elements that are in either group A or B, and in either group X or Y. Since nothing is in both groups A and B, or in both groups X or Y, we’ll instead use a simple chart, which looks like this:

Trigger: Group question
with no “Both Group A and
B” elements.

Response: Draw Group
Table:

These questions often involve elements that have two different qualities. For instance, cupcakes that are either vanilla or chocolate, and either frosted or unfrosted. Notice that there’s no overlap within each group: A cupcake can’t be both vanilla and chocolate, and it can’t be both frosted and unfrosted. We could have vanilla frosted cupcakes, vanilla unfrosted cupcakes, chocolate frosted cupcakes, or chocolate unfrosted cupcakes.

Here’s an either/or question example.

Question 10 of 20

Out of the 12,000 students and faculty at a certain university, there are 5 times as many students as there are faculty. There are 200 more female faculty members than there are male faculty members. If the university contains a combined total of 6,425 male students and faculty, how many female students are there?

Here’s How to Crack It

Since you can be either a student or faculty and either male or female, and there’s no overlap in the question, we can draw our Group Table. It should look like this:

Now let’s take the question apart in bite-sized pieces. The first thing we find out is that there are 5 times as many students as faculty. If we say there are f total members of the faculty, then 5f = s. Now that we know there’s a total of 12,000 faculty and students, 12,000 = f + s. Substituting in our earlier equation, we get 12,000 = f + 5f. Since 12,000 = 6f, f = 2,000. Since there are 2,000 faculty members, there are 10,000 students.

Now we can use the next piece of information: There are 200 more female faculty members than there are male faculty members. There are 2,000 total, so m + w = 2,000. We know that w = 200 + m, which we can plug into our earlier equation to get m + 200 + m = 2,000, so m = 900. If there are 900 male faculty, there are (2,000 − 900) 1,100 female faculty.

Okay, we’ve got one more piece to use: There’s a total of 6,425 males. There’s a total of 12,000 students and faculty, which means there are 12,000 − 6,425 = 5,575 females. Filling that into our chart, we get:

Now we can easily fill in the rest of the table with simple subtraction: The 6,450 − 900 = 5,550 males, and the number of female students is 5,575 − 1,100 = 4,475. The answer to the question is 4,475. (You don’t need to know the number of male students to answer the question, but for the sake of completeness, 6,425 − 900 = 5,525 male students.)

STANDARD DEVIATION

Standard deviation means almost exactly what it looks like it means: deviation from the “standard,” or mean, value of a set of numbers. A normal distribution of data means that most of the numbers in the data are close to the mean while fewer values spread out toward the extremes. The bigger the deviation from the norm, the wider the spectrum of numbers involved.

The Bell Curve

A normal distribution is best displayed in the form of a regular bell curve, which looks like this:

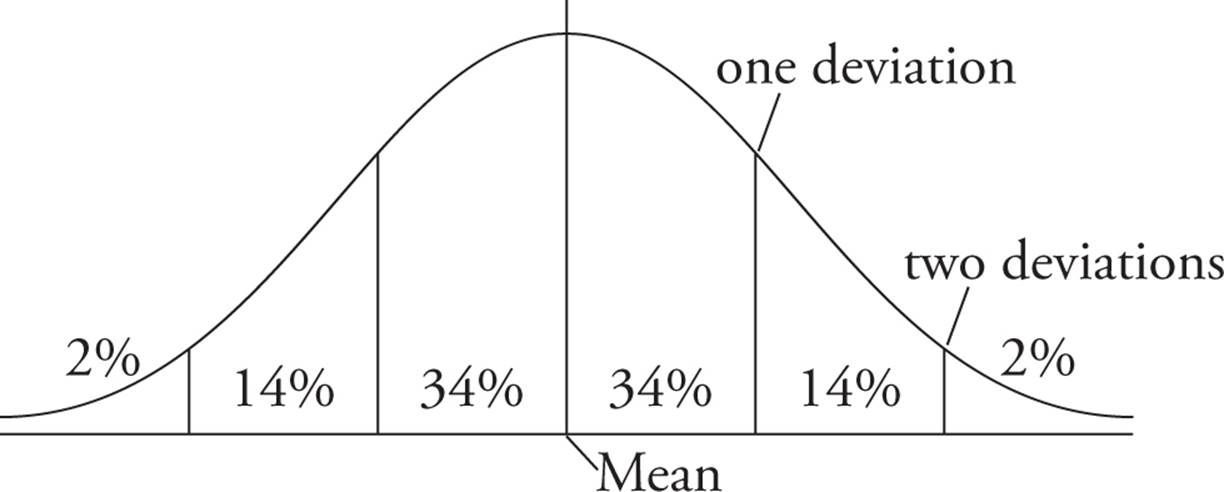
The mean is the middle number, right at the 50% mark. The GRE will either just present you with the mean straight up, or it will be one quick calculation away. The rest of the lines on the curve represent standard breakpoints at 34%, 14%, and 2% of the data values. These mean that, within a normal distribution, 68% of the values (34% on the left, 34% on the right) are within one standard deviation from the mean.

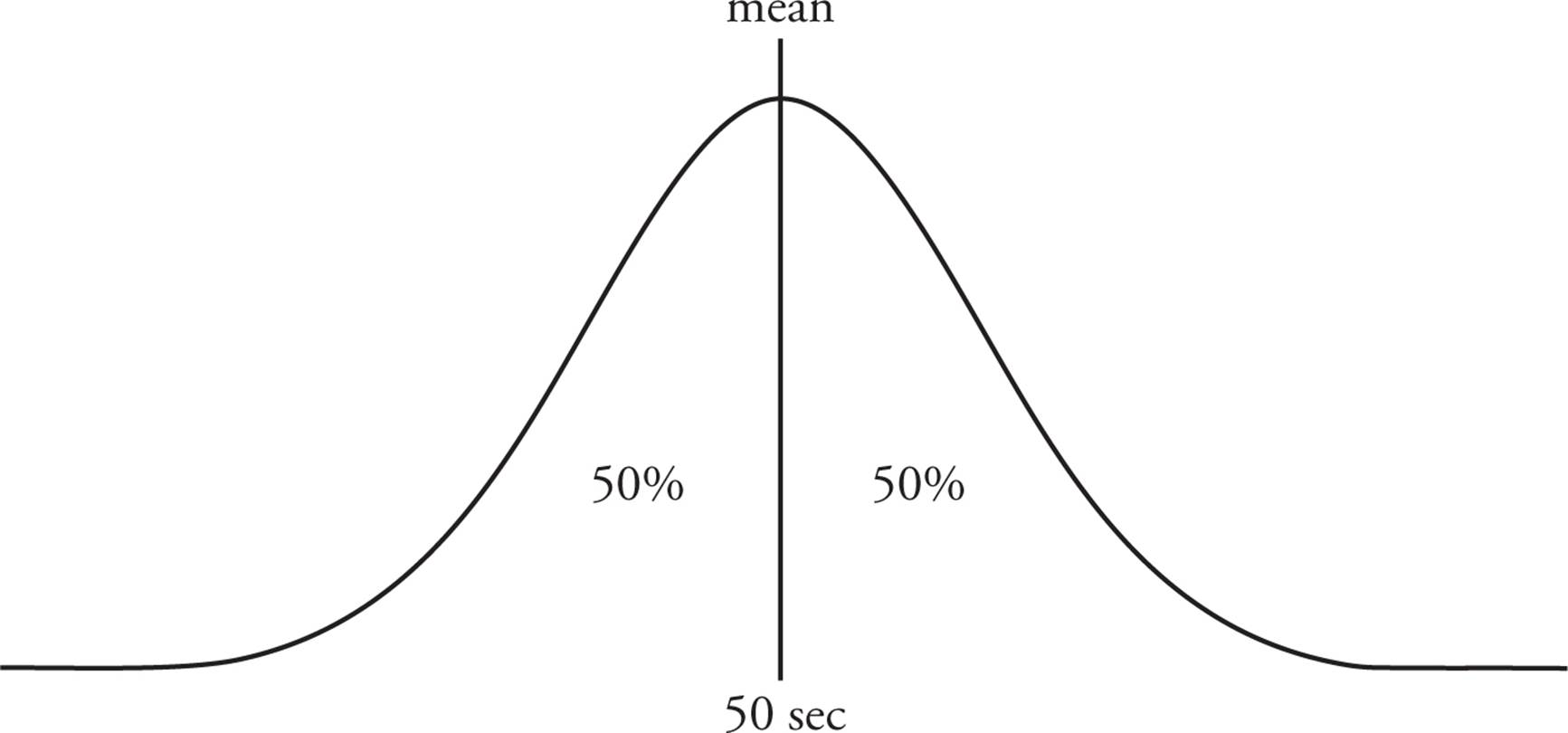
To explain the normal distribution, let’s use a sample data set. Say we asked 1,000 people to see how long they could hold their breath. After measuring all those people, and watching all those faces turn purple, we calculated that the average (arithmetic mean) number of seconds that people could hold their breath was 50. We then handed our data to a statistician friend, who calculated that our data followed a normal distribution and the standard deviation was 15 seconds.

Since the mean time was 50 seconds, half of the people were able to hold their breath for less than 50 seconds and half the people were able to hold their breath for longer. Our data looks something like this:

Trigger: Question
contains the words
“normal distribution” or
“standard deviation.”

Response: Draw a bell
curve and label the mean
and the 34-14-2 points for
each standard deviation.

Most people were able to hold their breath close to 50 seconds, and as we get farther away from 50 seconds the number of people drops off substantially in both directions. That’s what’s important about a normal distribution. The data points are distributed in this nice, predictable bell curve shape.

Here’s where our standard deviation and 34-14-2 pattern comes into play. Since our standard deviation is 15 seconds, that means that 34% of people held their breath between 50 and 65 seconds. Those people were 1 standard deviation or less from the mean. When we move another standard deviation (another 15 seconds) away, we find that only 14% of people could hold their breath for anywhere between 65 and 80 seconds. Only 2% of people (all of whom have excellent lungs and do plenty of cardio) could hold their breath for more than 80 seconds.

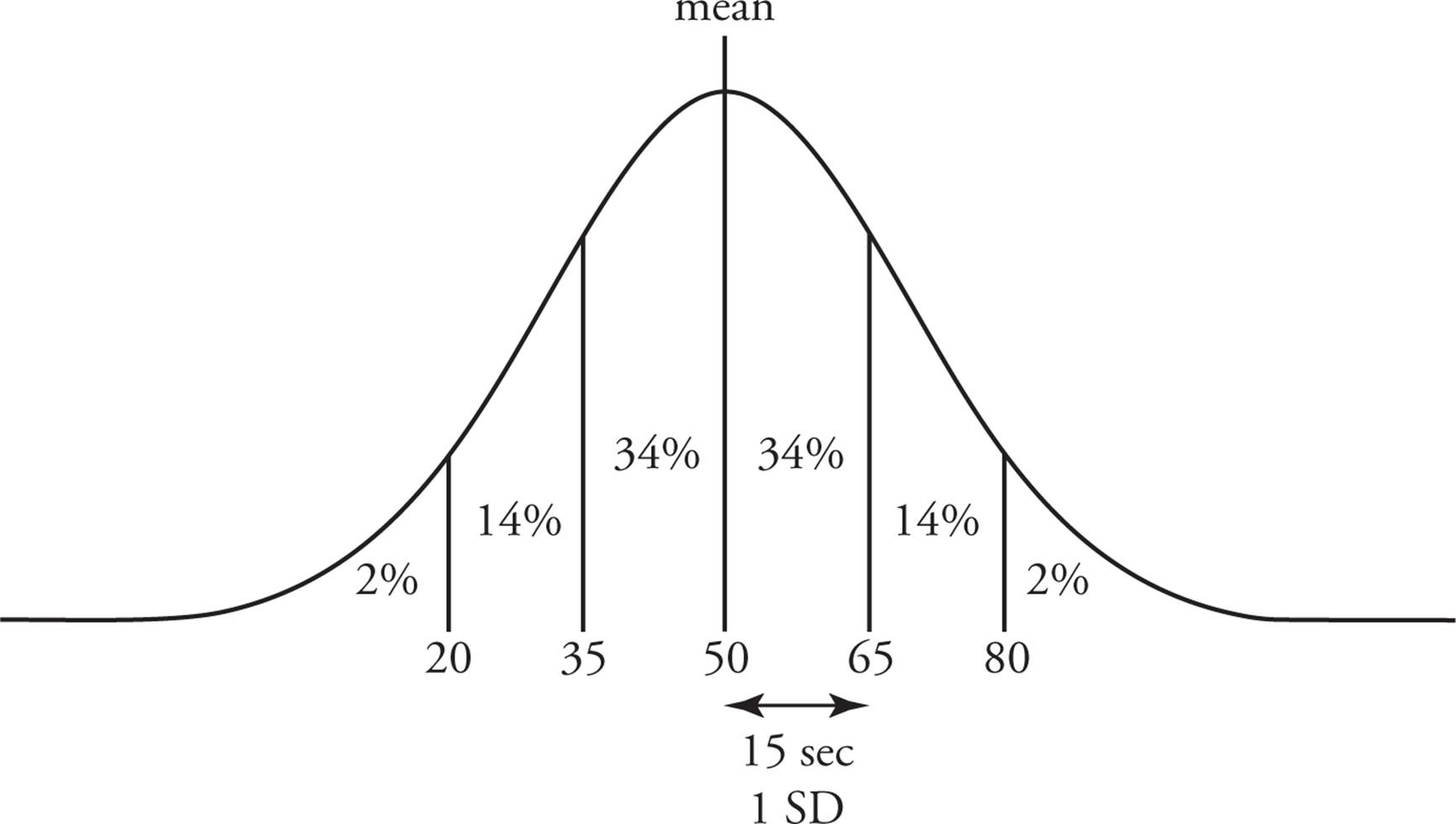
The same holds true in the other direction. 34% of people surveyed were able to hold their breath for anywhere between 35 and 50 seconds. Those people were 1 standard deviation or less from the mean. As we move another standard deviation of 15 seconds away, we find that only 14% of people could hold their breath for between 20 and 35 seconds. Finally, we have the bottom 2% of people. These people are 2 standard deviations or more below the mean, which is another way of saying that they are the absolute worst at holding their breath.

You will never have to calculate the standard deviation directly from the data on the GRE, but you will have to understand how it works.

· The bigger the standard deviation, the more spread apart the numbers. Imagine an unkept field. If we went out and measured the height of the grass in that field, we’d probably get a standard deviation of about 20 centimeters or so: We’d have some really tall grass, but also some young, short grass. Due to those variations in height, we’d have a large standard deviation. The height of grass wouldn’t always be too close to the mean. Now imagine we took a lawnmower to that field. The lawnmower wouldn’t cut every blade of grass to the exact same height, but it would make every blade fairly close to the same height. Our standard deviation would shrink from 20 cm to 1 cm. Sure, some grass is a little taller than our mean height and some is a little shorter, but overall the heights of the blades of grass are very close to being the same. There aren’t many variations in height, so we have a small standard deviation. Lots of tall grass, short grass, and medium grass meant a large standard deviation, but when all of our grass was close to the same height we had a small standard deviation.

· The more standard deviations away from the mean, the “stranger” you are. Say that the average pop song is three minutes long, with a standard deviation of 30 seconds. A song that is 3:30 isn’t that weird, because it’s only 1 standard deviation away from the mean. A song that’s 3:45 is a little more unusual, because it’s 1.5 standard deviations from the mean. A song that’s 4:30 long is really weird, because that’s 3 standard deviations away from the mean. For a pop song, it’s really unusual to be that long. Compare that to the opera. The average opera is 90 minutes long, with a standard deviation of 25 minutes. A two-hour (120 minute) long opera, therefore, isn’t that weird: It’s a little more than 1 standard deviation away from the mean. But how about a five-minute opera? That’s around 3.5 standard deviations below the mean. For an opera, that’s freakishly short.

That’s all you need to know about standard deviation. Sometimes, in fact, the GRE will even give you 34-14-2 pattern and a drawing of the bell curve, but you should still memorize 34-14-2 and remember that the bigger the standard deviation, the more spread apart the numbers, and that the more standard deviations away from the mean, the “stranger” you are.

Question 16 of 20

The average age among members of a retirement community is 61, and the standard deviation is 2.5 years. Under a normal distribution, what percent of the community members are younger than 56 years old?

2%

16%

32%

34%

50%

Here’s How to Crack It

If the average age is 61 and the standard deviation is 2.5 years, then a person who is 56 years old is 2 deviations from the mean (2 × 2.5 is 5, and 61 − 5 = 56). This means that only the bottom 2% of the group are less than 56 years old. The answer is (A).

Your scratch paper should look like this:

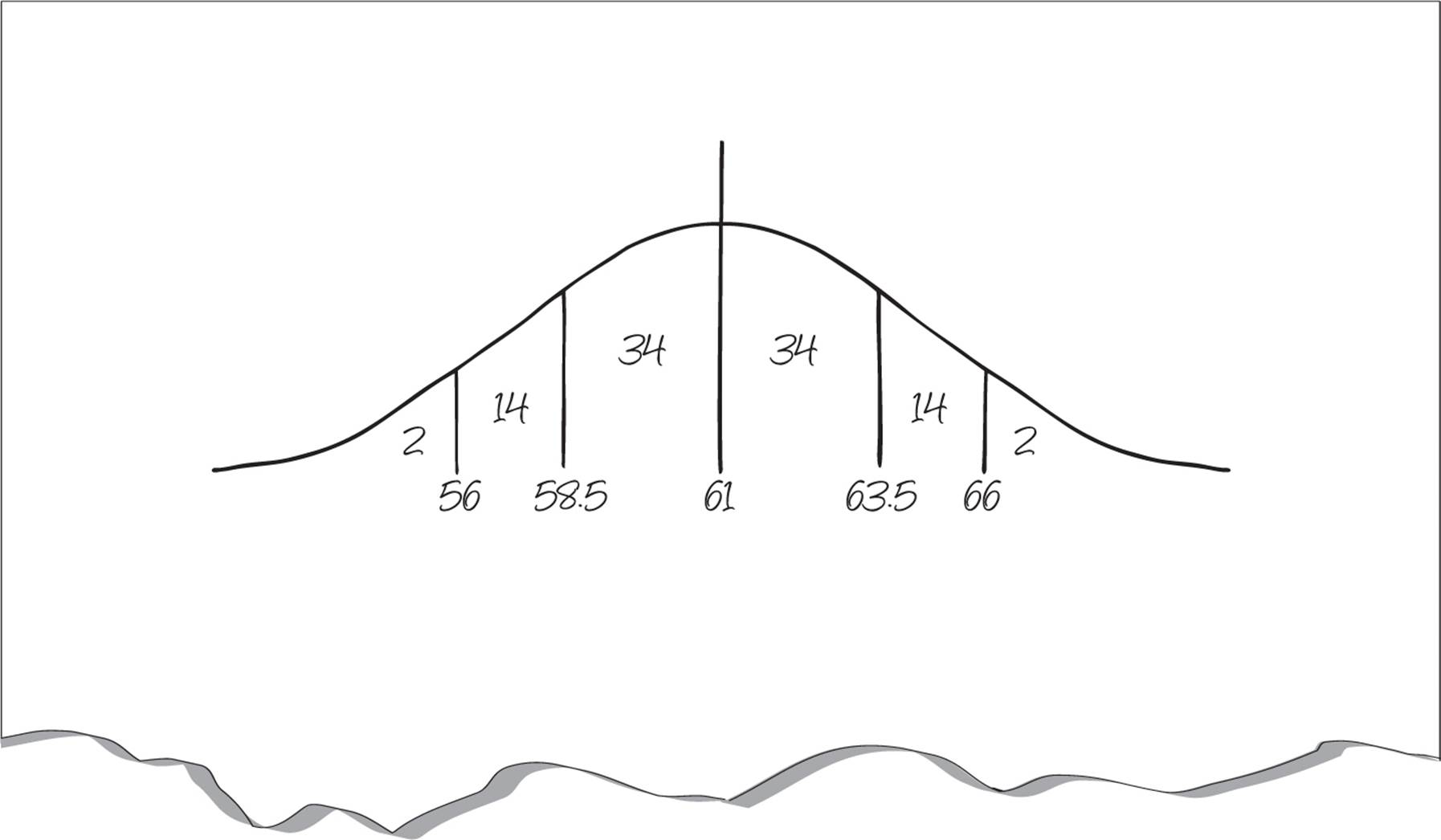
ARRANGEMENTS AND COMBINATIONS

We’ve got one last topic to cover. It doesn’t come up often, so if you’re not completely comfortable with Plugging In, PITA, and all those other topics, you should go back and review those first.

Comfortable so far? Okay, so let’s talk about arrangements and combinations. Arrangements and combinations questions typically ask about the number of different ways of either arranging things or grouping things. For these questions, we’ll pretend that we’re arranging or grouping our items piece by piece, item by item, element by element.

Each time we have to choose something, we’ll figure out how many options we have. Then we’ll pretend we chose one, and now have to choose the next thing. Once we’ve figured out how many choices we had at each point, we’ll multiply those numbers together.

Let’s do an easy example first. Pretend you have three pictures, one of Groucho, one of Harpo, and one of Chico, that you need to place on a shelf. To find the number of different ways to arrange those pictures, you could simply write out all the different possibilities. We could have Groucho, Harpo, and then Chico, or we could have Groucho, Chico, then Harpo. We could also have Harpo, Groucho, Chico, or Harpo, Chico, Groucho, or Chico, Harpo, Groucho, or Chico, Groucho, Harpo. That’s six different ways of arranging those pictures.

So let’s look at how we listed our original set of three pictures, and do some math. We have three different choices we have to make: Who is going in the first spot on the wall, who is going in the second, and who is going into the third. Because we have three choices to make, we’ll draw three slots (short horizontal lines to put numbers in) on our scratch paper, like so:

Trigger: The phrases
“arrangements,”
“permutations,”
“combinations,” “different
ways,” “many ways,” or
“different groups” appear
in the problem.

Response: Draw a
horizontal line for each
choice we have to make.

The first thing we had to decide was whether to put Groucho, Harpo, or Chico first. We had three different options of whom to place in that first spot, so we’ll put three in the first slot on our scratch paper:

Notice that once we choose Groucho to go first, we have only two options left: Does Harpo go next, or does Chico? The same is true whether we put Harpo or Chico first; we have only two options for that second slot. Put a 2 on that second spot.

Once we’ve put Groucho in the first spot, and Harpo in the second, we’ve got to put Chico last, right? Or, say we put Harpo in the first spot and Chico in the second: In that case, Groucho’s got to be last. Since, no matter whom we place in the first two spots, we’ve only got one option (whoever is left) for the last spot, put a 1 in the last slot.

Now multiply those numbers together. 3 × 2 × 1 = 6. Six different ways, exactly how we calculated when we listed everything out earlier.

Each time we had a choice to make, we looked at how many options we had for that choice. As we moved through our choices, we had fewer options, because we pretended that the previous choices had been made.

Try the next problem.

Question 8 of 20

Eight horses compete in a race. The first horse to finish wins a blue ribbon, the second wins a red ribbon, and the third wins a yellow ribbon. In how many ways can the ribbons be awarded?

Here’s How to Crack It

The end of the problem states in how many ways, which means this is an arrangement question. We’ve got 3 ribbons to give away, so draw 3 slots on your scratch paper. For that blue ribbon, we could give it to whichever of those 8 horses comes in first, which means we’ve got 8 options for our first slot. Once we’ve given one of the horses a blue ribbon, there are only 7 horses left to win the red ribbon, so put a 7 in the second slot. Now there are 6 horses left to win the yellow ribbon, so put 6 in the third slot. We now have 8 × 7 × 6 = 336 different ways of awarding those ribbons.

If a problem contains restrictions on what we can choose at certain points, we’ll start with those restricted positions first, and then deal with everything else. It’s as though you were seating guests around a table. If you knew that two people just really, really, hated each other, then the first thing you’d do is make sure they sat on opposite ends of the table. Once that’s taken care of, you’d then place the rest of your friends in the remaining seats.

Question 13 of 20

Boone is making a playlist of 5 songs, but only 2 are suitable to be last. How many different playlists could Boone make?

24

48

60

120

3,125

Here’s How to Crack It

The problem asks for how many different lists, so this is another arrangement question. We’ve got 5 songs we need to put in order, so draw 5 slots on your scratch paper. Here, however, we’re limited into what can go in the last spot in our list: It’s got to be one of 2 possible songs. So we’ll start by putting 2 in the last slot.

Now we can deal with the other slots. Since we have no other restrictions, let’s continue by going back to the first slot. Since we put one of our songs in that last spot, we have only 4 songs left to put in the first slot:

The second slot therefore has only 3 songs possible, because we’ve already placed songs in the first and last slots. Continuing to fill out the slots, we get:

Multiplying 4 × 3 × 2 × 1 × 2 gives us 48, answer (B).

The questions we’ve done so far are all arrangement questions, because the order in which our elements are placed matters. Putting our Chico picture before our Harpo picture would be different from putting Harpo before Chico. Switching the first and second place ribbons of two of the horses would mean a different outcome of the race. Switching the middle songs of Boone’s playlist would mean a different play-list than we had originally. Arrangement questions are questions in which order matters.

What about when order doesn’t matter? Those are called combination questions, and they often contain words such as “groups,” “teams,” or (obviously), “combinations.” If you had to choose two books to loan, at the same time, to a friend, it wouldn’t matter if you loaned your friend Pale Fire and The Tin Drum as opposed to loaning her The Tin Drum and Pale Fire. Either way, she’s borrowing the same two books.

Since order doesn’t matter on combination questions, we’re going to add one extra step at the end. We need to get rid of the repeat groupings, so we’ll divide our answer by the factorial of our number of slots. An easier way to think of it is that we’ll count down to 1 underneath our slots.

Trigger: The words
“team,” “groups,”
“combinations,” or order
doesn’t matter.

Response: At the end of
the problem, divide the
answer by the factorial of
the number of slots.

Question 2 of 20

A group of 4 is to be chosen from among 9 total employees.

Quantity A is greater.

Quantity B is greater.

The two quantities are equal.

The relationship cannot be determined from the information given.

Here’s How to Crack It

Since we have a group of 4, we’ll draw 4 slots on our paper. We could choose one of the 9 people for the first slot, leaving 8 for the second slot, 7 for the third, and 6 for the fourth, giving us 9 × 8 × 7 × 6. However, we’re choosing groups of people, which means that the order we choose each group doesn’t matter. As long as it’s got the same people in it, who cares in what order those people were chosen?

Our last step, therefore, is to divide by 4! We’ll show this by counting down from 4 underneath each slot, making each number a fraction. We now have 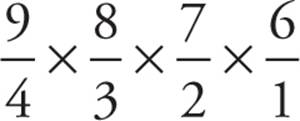, which we can simplify to 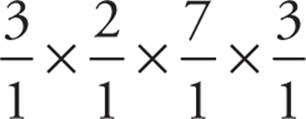= 126. Since Quantity A is larger than Quantity B, the answer is (A).

By the way, did you notice how the denominator of our fraction canceled out completely? That will always happen with combinations. Think of it this way: There will never be a fractional number of ways to select groups of people. If the denominators of the fractions don’t all cancel out to 1, you may have either made an arithmetic mistake, or missed a chance to cancel out.

To review, if order matters (“arrangements,” “schedules,” et cetera), then it’s an arrangement. Draw a slot for each time you need to make a choice, and then fill in each slot with the total number of options for each choice.

If order doesn’t matter (“groups,” “pairs,” “teams,” et cetera), then it’s a combination. Start the problem as you would an arrangement problem, but then divide by the factorial of the number of slots you have.

Permutations and Combinations Quick Quiz

Question 1 of 5

At a certain ice cream shop, a sundae contains two different scoops of ice cream. If the shop sells 20 varieties of ice cream, how many different sundaes are possible?

40

190

200

380

400

Question 2 of 5

A delivery driver must make 8 stops over the course of the night.

Quantity A is greater.

Quantity B is greater.

The two quantities are equal.

The relationship cannot be determined from the information given.

Question 3 of 5

A website requires a password made up of 2 one-digit numbers followed by 3 of the 26 letters. How many different passwords are possible if repetition of numbers and letters is allowed?

98

17,576

117,000

1,404,000

1,757,600

Question 4 of 5

A chef has lamb, carrots, potatoes, celery, and peppers. From these, she chooses three different ingredients for a stew. She will serve the stew with bread, salad, or dumplings. How many different meals could the chef serve?

Question 5 of 5

Ten runners compete in a race. The first 6 to finish receive a $100 prize. In addition, the first 3 to finish receive medals: gold for first, silver for second, and bronze for third.

Quantity A is greater.

Quantity B is greater.

The two quantities are equal.

The relationship cannot be determined from the information given.

Explanations for Permutations and Combinations Quick Quiz

1. Since each sundae contains two scoops of ice cream, draw two slots on your scratch paper: __ __. There are a total of 20 different flavors, so we have 20 options for our first slot: 20 __. The problem states that the sundae must have two different types of ice cream, so we can’t have the same flavor in the second spot as in the first. Therefore, there are only 19 different options left for our second choice: 20 19. Before we multiply, we have to ask ourselves if order matters. Would a sundae with a scoop of chocolate and a scoop of vanilla be different than a sundae with a scoop of vanilla and a scoop of chocolate? Nope. Order doesn’t matter, so this is a combination. Therefore, we’re going to divide by a factorial of 2 underneath our slots, giving us 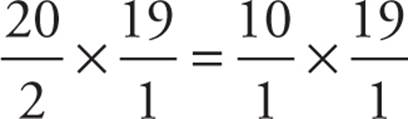= 190, answer (B).

2. As the driver decides his route, he’s going to have 8 choices to make: Which stop to make first, which to make second, and so on. Draw 8 slots on your scratch paper: __ __ __ __ __ __ __ __. For his first stop, he has 8 options of where to stop, so put an 8 in the first slot. Once he’s made that stop, he has only 7 options left for the second stop, so put 7 in the second slot. Continuing to fill in the slots, we have 8 7 6 5 4 3 2 1. Does order matter? Definitely. If the driver stops at House A before House B, that’s a different route than if he stops at House B before House A. This an arrangement. Since order matters, we can multiply together 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1, using the calculator and scratch paper, giving us 40,320. Since the quantities are equal, the answer is (C).

3. The password has 5 total numbers or letters, so we’ll have to make 5 choices. Draw 5 slots on your scratch paper: __ __ __ __ __. The first thing we’ll have to choose is a one-digit number. Since there are 10 one-digit numbers, from 0 to 9, we have 10 options for our first slot. We also need to place a one-digit number in the second spot. However, since the problem states that repetition is allowed, we have 10 options for our second slot as well. In other words, if we choose 4 as the first character of our password, we’re allowed to choose any one-digit number, including 4, as the second character. So far, we’ve got 10 10 __ __ __. Now we get into the alphabet. Our first letter could be any of the 26 letters, so put 26 in the third slot. The second letter could also be any of the 26 letters, since repetition is allowed, so put 26 in the fourth slot. The last character of our password also needs to be a letter, with repetition allowed, so put 26 in the last spot. Our slots are now 10 10 26 26 26. Does order matter? Having 12ABC as a password is different than having 21CBA, so order definitely matters. Multiply together the numbers in our slots: 10 × 10 × 26 × 26 × 26 = 1,757,600, answer choice (E).

4. This is a slightly more difficult problem, because we’ve got two overall decisions to make: which stew to serve and with what to serve it. Just choosing the stew itself will take some math. The chef has 3 options of what to put in the stew, so we have 3 slots: __ __ __. There are 5 ingredients, so we have 5 options for the first slot. Since we must use 3 different ingredients, we have only 4 options left for the second slot, 3 options for the third slot, and our slots are 5 4 3. Does order matter? Putting lamb, celery, and potatoes in the stew is the same as putting potatoes, celery, and lamb, so order doesn’t matter, so this portion of the problem is a combination. Therefore, we have to divide by the factorial of 3 underneath our slots, giving us 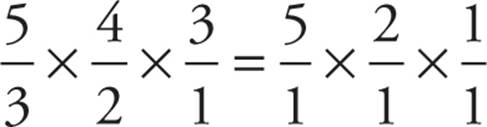= 10 different stews. Now we have to decide our different meals. We’ll have to choose a stew and a side, so we have two slots: __ __. For our first slot, we have the option of any of those 10 delicious stews we calculated earlier. For our second slot, we can choose 1 of those 3 sides. The slots are 10 3. Does order matter? Definitely, because we’ve got two different types of items here: We can’t serve dumplings as a stew, and we can’t serve a stew in place of bread. 10 × 3 = 30 different meals.

5. Let’s focus on Quantity A first. We’re giving away 6 prizes, so we have 6 slots: __ __ __ __ __ __. For the first slot, we can give the prize to any of the 10 runners in the race. Once we’ve given away that prize, we only have 9 runners left who can receive a prize, and so on, giving us 10 9 8 7 6 5. Does order matter? Well, if I come in first and get $100, is that any different than coming in sixth and getting $100? No, since I’m getting $100 either way. Since order doesn’t matter, this is a combination question, and we’ll have to divide by the factorial of 6 underneath our slots: 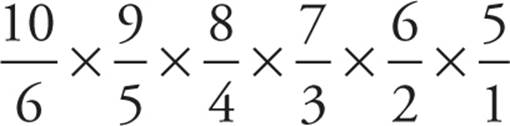. Before you multiply, see which denominators cancel out with which numerators, and we have 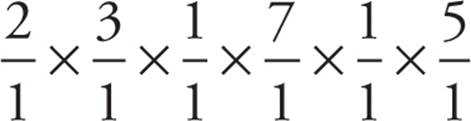= 210 different ways of handing out the six $100 prizes.

Now let’s work on Quantity B. We have 3 medals to give away, so we’ve got 3 slots: __ __ __. The gold medal could go to any of the 10 runners, so put 10 in the first slot. The silver medal can go to any of the remaining 9 runners, and the bronze can go to any of the remaining 8 runners, so the slots are 10 9 8. Does order matter? If two runners, Dave and Rob, compete and Dave wins the gold medal and Rob wins the bronze, is that the same as Rob winning the gold and Dave winning the bronze? Nope, so order matters. This is a permutation and we have to multiply together the slots: 10 × 9 × 8 = 720. Quantity B is larger than Quantity A, so the answer is (B).

Congratulations! You’ve made it through the most arcane topics that the GRE tests. If you can handle yourself here, you’re in great shape for the quantitative section. Though these topics are tested infrequently, knowing this stuff could mean the difference between a good score and a great one.

Be sure to keep practicing; you’re almost ready to take the test and get on with your life!

The Rest of the Story Drill

Question 1 of 15

All but 4 of the counselors on staff at a certain summer camp have sailing certification, first aid certification, or both. Twice as many counselors have neither certification as have both certifications, and 7 counselors have sailing certification. If there are a total of 22 counselors on staff, then how many of the counselors have first aid certification?

Question 2 of 15

What is the value of ?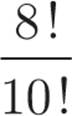

9!

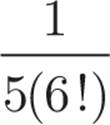
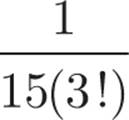
Question 3 of 15

If set X = {12, 16, 20}, then which of the following sets has a standard deviation greater than that of set X ?

{2, 4, 6}

{4, 5, 6}

{13, 16, 19}

{20, 32, 44}

{95, 100, 105}

Question 4 of 15

Ryan’s bakery has 212 cakes to sell. 131 cakes are chocolate and the rest are vanilla while 104 cakes have mocha frosting, and the rest have coconut frosting. If 37 of the chocolate cakes have mocha frosting, how many of the vanilla cakes have coconut frosting?

14

67

81

104

108

Question 5 of 15

If a value for the integer x is randomly selected and −10 < x < 10, what is the probability that x is even?

Question 6 of 15

Which of the following is the least value of x for which is an integer greater than 1 ?

2

3

6

7

12

Question 7 of 15

The purchaser of a certain car must choose 2 of 5 special options and 5 of 6 interior features. How many different combinations of options and features are available to the purchaser?

10

16

18

30

60

Question 8 of 15

Laura has decided to display 5 of her glass animal figurines on a shelf. If she has 6 circus animals and 5 farm animals from which to choose, and she wants a farm animal in the middle of the display, then how many arrangements of the figurines are possible?

30

150

3,024

25,200

30,240

Question 9 of 15

Two six-sided dice with sides numbered 1 through 6 are rolled. If the two resulting numbers are multiplied, what is the probability that their product will be even?

Question 10 of 15

Sandy is designing an internet banner advertisement and has decided to use one background, one font, two different accent images, and four different colors. If Sandy has 5 backgrounds, 4 fonts, 6 accent images, and 12 colors from which to choose, then how many different banners can she make?

Question 11 of 15

The Outdoor Adventure Camp offers 1-week sessions. During the first week, 44 campers go fishing, 33 go orienteering, and 37 do neither activity. The same number of campers goes orienteering in week 2 as in week 1, and 15 campers in week 2 do both activities. If 49 of the 120 campers who attend week 2 do neither activity, and twice as many campers attend week 1 as go fishing in week 2, then how many total campers attended these 2 weeks?

196

226

234

360

662

Question 12 of 15

During this year’s fundraiser, students who sell at least 75 subscriptions will win a prize. The fourth-grade students sold an average of 47 magazine subscriptions per student, and the sales have a standard deviation of 14. If the sales of subscriptions are normally distributed, then what percent of the fourth-grade students will receive a prize?

0.02

0.25

2

25

It cannot be determined from the information given

Question 13 of 15

A college admissions committee must select candidates for a certain program from among high school applicants and transfer applicants. The committee has already chosen 132 female candidates in a 3 to 1 ratio of high school students to transfer students, and will maintain this ratio in the selection of male candidates. If the final class size must be between 325 and 350 students, then which of the following is an acceptable number of male high school applicants for the committee to choose?

Indicate all such values.

99

144

156

162

168

180

Question 14 of 15

Robin and Terry want to invite 5 of their friends to their wedding. Robin has 7 friends, Terry has 6, and Robin and Terry have no friends in common. If at least 1 of Robin’s friends and at least 1 of Terry’s friends must be invited, how many different groups of friends could Robin and Terry invite to their wedding?

462

924

1,260

2,520

151,200

Question 15 of 15

Tony’s political science final exam consists exclusively of 8 true/false questions. If Tony guesses on every question, what is the probability that he gets exactly 7 questions right?

EXPLANATIONS FOR THE REST OF THE STORY DRILL

1. 13

First, write down the group formula, Total = Group₁ + Group₂ + Neither − Both, and fill in what you know. If sailing certification is Group₁ and first aid certification is Group₂, then 22 = 7 + Group₂ + 4 − 2. So, 22 = Group₂ + 9, and you can solve for Group₂ = 13.

2. E

8! = 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1, and 10! = 10 × 9 × 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1. When dividing 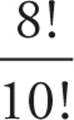, everything but 10 × 9 in the denominator cancels out, and you have 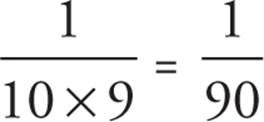. For choice (A), 4 × 3 × 2 × 1 cancels out of the top and bottom, leaving . Choice (B) is 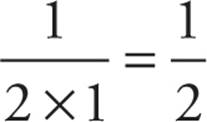. Estimate that choice (C) is greater than 1, and you need an answer less than 1. Choice (D) is 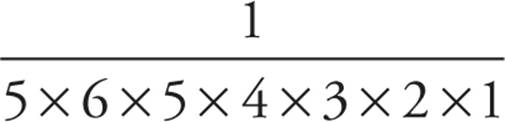. Estimate that the denominator is greater than 90. Choice (E) is .

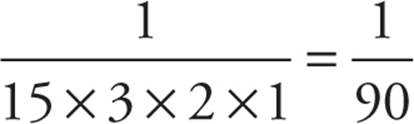3. D

Don’t calculate anything on this one. Instead, just remember that standard deviation is a measure of how much numbers in a set vary, or deviate, from the average, or standard. Since all of the sets contain three equally spaced numbers, the middle number in each case is the average. The other two numbers in the correct answer, choice (D), differ most from their average.

4. A

Take this problem one step at a time, using a grid layout. 131 cakes are chocolate, so 81 must be vanilla. 104 have mocha frosting, so 108 have coconut frosting. 37 chocolate cakes have mocha frosting, so there are 94 chocolate cakes with coconut frosting, leaving 14 vanilla cakes with coconut frosting.

5. D

There are 19 integers in the range between −10 and 10. Of those, 9 are even. The probability of selecting an even number is .

6. D

It’s an algebra question with numbers for answer choices, so set up your scratch paper to Plug In the answers. Start with choice (C): if x = 6, then 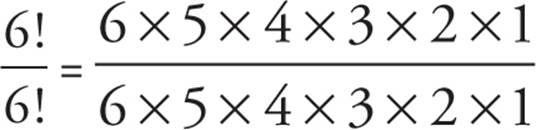= 1; choice (C) is too small, so eliminate choices (A), (B), and (C). Now do the same thing for x = 7; all the numbers will cancel out of the denominator, and you’ll be left with 7 in the numerator, so the whole expression equals 7. Choice (D) is correct. Choice (E) yields an integer as well, but isn’t the least value among the choices to do so.

7. E

The purchaser has 5 options to choose from for his first choice of special options and 4 left to choose from for his second choice. 5 × 4 = 20, but because the order of choice doesn’t matter, divide that 20 by the factorial of 2 to get 10 special option groupings. Do the same thing for the interior features: 6 × 5 × 4 × 3 × 2 = 720. Divide 720 by (5 × 4 × 3 × 2 × 1) because the order of choice doesn’t matter. Multiplying the 10 special options by the 6 interior features yields 60 possible option groupings.

8. D

There are 5 spaces to fill with a restriction on the middle space, so start with the restricted space. The middle space must be a farm animal, and there are 5 potential figurines for that spot, so 5 goes in that space. The remaining spaces are unrestricted, so there are 10 figurines (6 circus and 4 remaining farm animals) left from which to choose. Slot your first of four remaining spaces with 10, then 9, 8, 7 for the remaining spaces as each one fills. 10 × 9 × 5 × 8 × 7 = 25,200, making choice (D) the best answer. Choice (E) is a trap answer if you don’t account for the restricted space.

9. D

The only outcome that would not result in an even product is two odd numbers, because even × (even or odd) = even. Subtracting the probability of two odd rolls from 1 will give the probability that the product is even because P(odd product) + P(even product) = 1. The probability that a roll will be odd is , or . The probability that both will be odd is 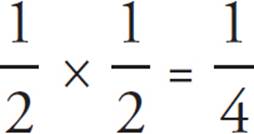. The probability that the product will be even is 1 − .

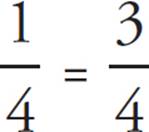10. 148,500

This is a tricky combination question because you have to treat each category as its own combination, and then multiply the results. Find the number of ways you can choose 1 out of 5 backgrounds, 1 out of 4 fonts, 2 out of 6 images, and 4 out of 12 colors, and then multiply those results together. So, 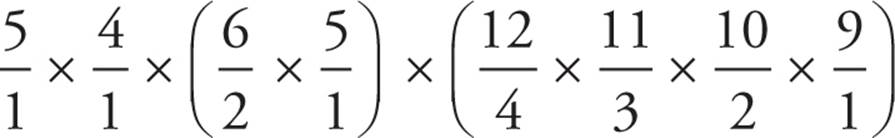= 148,500.

11. B

The question mentions neither and both, so be sure to write out the group formula, Total = Group₁ + Group₂ + Neither − Both, for each week. Let fishing be Group₁ and orienteering be Group₂, and fill in what you know: for week 1, you have Total = 44 + 33 + 37 − Both; for week 2, you have 120 = Group₁ + 33 + 49 − 15. Solve for Group₁ in the latter equation, and 53 people went fishing in week 2. Twice that many, or 106, attended week 1 overall, and over the 2 weeks the camp was attended by a total of 106 + 120 = 226 people.

12. C

When you see the words standard deviation or normally distributed, draw your bell curve and fill in the percentages: 34, 14, and 2. The average of 47 and a standard deviation of 14 means 75 is 2 standard deviations above the mean, so 2 percent of the students will receive a prize.

13. C and D

Since you have two traits (female/male and high school/transfer), use the group chart to organize your information. First find the acceptable range of the total number of male applicants to be 193−218: 325 total minimum − 132 female = 193, and 350 total maximum − 132 female = 218. Since the question asks for the number of male high school applicants, plug the choices into your chart to solve for the number of male transfer students using the ratio. Then solve for the total number of male applicants to check if it is within the 193−218 range. In Choice (C), the number of male high school applicants is 156, divided by 3 since the male applicants are in a 3 to 1 ratio, and you get 52 male transfer applicants. 156 + 52 = 208 total male applicants, which is within the acceptable range. In Choice (D), the number of male high school applicants in now 162. Divide 162 by 3 to get 54 for the number of male transfer applicants. 162 + 54 = 216, which is also within the acceptable range. Choices (B), (E), and (F) are all either too big or too small. Choice (A) is a trap answer in that it is the number of female applicants, and Choice (G) is also incorrect since it represents the lower range of the total number of male applicants.

14. C

In this question, the order in which the friends are invited does not matter, so you’re dealing with a combination. With a total of 13 friends between them and 5 slots to fill, Robin and Terry could invite 13 × 12 × 11 × 10 × 9 divided by the factorial of 5 = 1,287 groups of 5 friends to their wedding. There are 7 × 6 × 5 × 4 × 3 divided by the factorial of 5 = 21 groups that consist of only Robin’s friends, and 7 × 6 × 5 × 4 × 3 × 2 divided by the factorial of 5 = 6 groups that consist of only Terry’s friends. Subtract these two numbers from 1,287, and find that there are 1,260 possible groups that contain at least one of Robin’s friends and at least one of Terry’s. Therefore, choice (C) is the correct answer.

15. A

To find the probability of exactly seven correct choices, think about all of the possible combinations of eight answers with one wrong (W) and seven right (R) choices. For example, Tony could get WRRRRRRR, RWRRRRRR, and so on. There are 8 different arrangements of one wrong and seven correct answers. The probability of choosing a correct answer for one question is , and the probability of choosing a wrong answer is the same. Thus, the total number of possible outcomes is 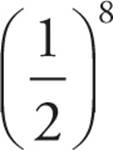. The probability of seven correct is the number of outcomes with seven correct divided by the total number of outcomes. The probability of exactly seven correct: 8 × .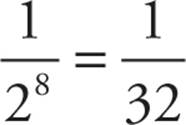