The Handy Math Answer Book, Second Edition (2012)

MATH IN ENGINEERING

BASICS OF ENGINEERING

What is engineering?

Engineering is a discipline that deals with the “art” or science of applying scientific knowledge to solve practical problems, usually in the areas of commerce and industry. Scientists ask the “why” of a question, then research the answer; in contrast, engineers want to know how to solve the problem and then how to implement the solution. But it’s not always easy to separate the two. Often a scientist has to use engineering basics (such as building special equipment for research), and engineers often have to do scientific research.

The word engineer (as well as engine) developed from the Latin root ingeniosus (“skilled”); in some languages, such as Arabic, the word for engineering also means “geometry.” The various branches of engineering include aerospace, agriculture, architectural, biomedical, computer, civil, chemical, electrical, environmental, mechanical, petroleum, and material science.

What types of mathematics are used in engineering?

Mathematics is definitely a necessity in engineering, especially the fields of algebra, geometry, calculus, and statistics. Certain divisions of engineering rely on variations of mathematics, including combinations of arithmetic, algebra, geometry, calculus, differential equations, probability and statistics, complex analysis, and others. For example, civil and structural engineers use a great deal of linear algebra and work with matrices. Mechanical engineers use logs and exponents, calculus, differential equations, and probability and statistics. And a chemical engineer uses such mathematics as algebra and geometry, logs and exponents, integral calculus, and differential equations.

What are some details of Jean Baptiste Fourier’s life?

The accomplishments of French mathematician and physicist Baron Jean Baptiste Joseph Fourier (1768–1830) prove that not all famous mathematicians did just math. Fourier was a teacher, became involved in the messy French Revolution, and was arrested for his views and imprisoned in 1794. For a time, he even feared the guillotine, but political changes resulted in Fourier being freed. By 1798 Fourier joined Napoleon’s army in its invasion of Egypt as a scientific adviser. After Napoleon lost the Battle of the Nile to Nelson and was confined to Malta, Fourier continued his work in Egypt, establishing educational facilities there and carrying out archeological explorations. Back in France with Napoleon in 1801, he supervised the draining of the swamps of Bourgoin and the construction of a highway from Grenoble to Turin. He also spent time writing Description of Egypt, a book that Napoleon edited, and included some historical rewrites (by the second edition of the book, Napoleon himself would be completely edited out of the text).

As if he wasn’t busy enough, during this time Fourier wrote his now-famous 1807 paper, On the Propagation of Heat in Solid Bodies, a mathematical work on the theory of heat that presented one of his major contributions: the Fourier series. But it was an uphill battle to get approval from his peers. In 1811 he submitted his 1807 ideas for a mathematics prize, along with additional work on the cooling of infinite solids and on terrestrial and radiant heat. Only one other entry was received, making Fourier’s work the obvious winner. Finally, by 1822, he published his 1811 essay, making the techniques of Fourier analysis available to everyone. To this day, the functions that he worked out have a multitude of applications in engineering, science, and mathematics.

What are interpolation and extrapolation?

Interpolation in mathematics involves finding a value (or outcome) of a function between already known values; in other words, it is a method of estimating the values in between sampled data points. Extrapolation in mathematics is estimating the value of a problem beyond the range covered by the existing data. Both methods are used a great deal in engineering.

What are the Fourier series and Fourier transforms?

The idea for the Fourier series and Fourier transforms was developed by French mathematician and physicist Baron Jean Baptiste Joseph Fourier (1768–1830). (For more about Fourier’s life and times, see above.)

A Fourier series was developed as an alternate method of expressing a function by the expansion of the function. It is actually a specific type of infinite mathematical series that involves trigonometric functions. More simply put, it is essentially an infinite sum of sine and cosine waves. The Fourier series is used in applied mathematics; the study of Fourier series is considered a branch of what is called Fourier analysis. In engineering and physics, it is used to split up periodic (or continuous) functions into a group of simpler terms; and in electronics, it is used to express the periodic functions seen in waveforms of communication signals.

When Napoleon Bonaparte led his army into Egypt, French mathematician and physicist Baron Jean Baptiste Joseph Fourier joined him and was a scientific adviser. Fourier also worked for Napoleon when he was involved in draining the Bourgoin swamps and building a new highway.

The Fourier transform is a mathematical operation that essentially changes a signal into its constituent frequencies. For example, think of the Fourier transform as a “translator” that, as the name implies, “transforms” the signal. If one plots the electrical signal from a loudspeaker playing music, one sees a wavy (or sine) line, also referred to as the frequency. These waves can be big, small, close together, or farther apart. The collection of notes one hears from the speakers is the Fourier transform of the signal going into the loudspeaker. A type of Fourier transform is the fast Fourier transforms, or FFTs. They can be used for computer applications, with the speed and efficiency of the algorithm used to do the transform being “fast.”

What is a finite element analysis?

A finite element analysis (also known as FEA or finite element method) is a powerful tool to solve problems in engineering, especially for heat transfer, fluid mechanics, and mechanical system problems. The FEA consists of a computer model of a material or design that is stressed; the outcome is then analyzed for specific results. In reality, the computer is conducting a numerical analysis technique used for solving differential equations, and relating it to stress in the engineering problem.

This technique was first developed in 1943 by Richard Courant (1888–1972), who used a form of FEA to find approximate solutions to vibrational systems. Early in the 1970s, only companies that owned expensive mainframe computers were using FEA, including the aeronautic, automotive, defense, and nuclear industries. Since the mid-1990s, however, use of FEA has grown with the advent of faster and cheaper computers with more memory. The results are more accurate, too, allowing various industries to analyze new product designs and refine existing products.

Why is finite element analysis important to many industries?

Finite element analysis (FEA) is important to various industries—especially those that need to predict failure of a structure, object, or material when under unknown stresses—because it allows designers to understand all of the theoretical stresses within the structure. This cuts manufacturing costs that would occur if a sample of the structure was actually built and tested.

FEA uses a complex system of points (nodes), making up a grid called a mesh. The mesh is programmed to contain all the material, properties, and other factors that constitute the structure and determine how it will react to certain load conditions, such as thermal, gravitational, pressure, or point loads. The nodes are then assigned a density throughout the material, all depending on the stress levels anticipated in a certain area. In general, points with more stress (such as corners of a building or contact points on a car frame) will usually have a higher node density than those with little or no stress. As researchers examine the results of the FEA, they learn how the structure responds to the various stresses. In this way, a prototype of the structure won’t have to be built until the majority of the theoretical “kinks” are worked out of the system.

What types of analyses interest engineers?

There are several types of analyses that interest engineers, all of which involve mathematical modeling. Structural analysis deals with linear and nonlinear models and stresses on a material. The linear models assume the material does not plastically deform (the remaining deformation after the load causing it is removed); nonlinear models stress the material past its elastic capabilities. The stresses in the material then vary with the amount of deformation. Vibrational analysis deals with possible resonance and subsequent failure. It is used to test a material that may experience random vibrations, impacts, or shocks. Fatigue analysis is used to determine the life of a material or structure. It shows the effects of occasional (periodic) or cyclic loading on a structure or object, pointing out where cracks or fractures are most likely to occur. Engineers measure heat transfer to determine a material or structure’s conductivity or thermal fluid dynamics. In this way, researchers understand how a material will respond to various hot and cold conditions—or even how it diffuses heat and cold—over time.

What is dimensional analysis?

Simply put, dimensional analysis is a way of manipulating unit measures using algebra to determine the proper units for a quantity that is being computed. For example, the units of length over time represent velocity in feet per second; acceleration is velocity over time. Thus, acceleration will then have units of feet per second per second, or feet per second squared.

What is the least squares method?

This mathematical procedure, called either the least squares method or the method of least squares, finds the best-fitting curve for a given set of points by minimizing the sum of the squares of all deviations from the curve. It is often used in engineering for fluid flow, certain elasticity problems, and diffusion and convection in materials.

Why is Laplace transform important in engineering?

Laplace transform is a way to solve linear differential equations and translate them into simple algebraic problems that are easier to solve. It was developed by French mathematician and theoretician Marquis Pierre-Simon de Laplace (1749–1827). Although it carries his name, the Laplace transform seems to have been first used by Denis Poisson (1781–1840) in 1815. Today, it is used extensively in electrical engineering problems.

How are modeling and simulation used in engineering?

Modeling and simulation have become an essential part of engineering on both a small and large scale. Because building any sized structure takes time and money, engineers often develop a mathematical model, a set of equations that describe what may happen to a structure if it is built the way it is represented by the model. Using a computer (or graphic) representation gives the engineers a three-dimensional view.

For example, before the International Space Station was built, engineers used mathematical modeling to simulate what the entire station would eventually look like in three dimensions. In this way, the engineers learned how the ISS would orbit the Earth, how solar energy could be used to run the ISS, and even how to allow the various international spacecraft to dock with the station. The computer was the only way to solve such problems without real-life testing. It quickly and easily solved a plethora of mathematical equations, especially using such mathematics as calculus and differential equations.

One application for modeling is for engineers studying water flow to design stronger, more durable bridge pilings.

Another more down-to-earth example is hydraulic modeling. Engineers need to know how the water will flow around and push on bridge pilings, how to control drainage in cities and along coastline, and even how water flows through a city’s culvert system. For example, the United States Geological Survey (USGS) often develops one-, two-, or three-dimensional computer models of bridges over certain major rivers. With such models they can understand such conditions as how the water surface elevations change (especially crucial for estuaries along the coast that are affected by the tides), the runoff from other creeks and drainage areas that flow into the river, and the velocity distribution of the river—for low and high flow events (flood conditions)—and how these conditions will affect the bridge. Such details can also help other engineers who deal with structures found around the river, such as dams, levees, and even how erosion and deposition of sediments affect the river’s floodplain.

Who was Oliver Heaviside?

English electrical engineer Oliver Heaviside (1850–1925) was a self-taught genius who made several contributions to the field of electricity and even atmospheric studies. In 1902 Heaviside predicted that there was a conducting layer in the atmosphere that allowed radio waves to follow the Earth’s curvature—a layer now named after him.

In electrical engineering, Heaviside was best known for operational calculus, a tool for solving linear differential equations with constant coefficients. It was usually applied to brief or fleeting (called transient) phenomena and was very similar to Laplace transform in its calculations. Although Laplace had developed his ideas almost a century before, Heaviside knew nothing of them, because they were not well-known during his time.

But Heaviside’s operational calculus did have its problems, as well as its critics. It was severely limited because of its lack of mathematical theory. This not only limited its applications, but also created many uncertainties and ambiguities in the equations and solutions. Today, operational calculus has been replaced by Laplace transform, especially in fields such as electrical engineering.

What is fluid mechanics?

Fluids are substances that flow, including gases and liquids. Fluid mechanics, or hydraulics, is the study of the physical behavior of these gases and liquids and their role in engineering systems. This includes the mathematics of the forces in and motion of substances, turbulence, wave propagation, and so on.

Most fluid mechanics problems in engineering are mathematically modeled using differential equations. These models can also be applied to other engineering areas, such as electromagnetism and the mechanics of solids (because solids still “move,” albeit slowly). Other fluid mechanical studies include the compressibility of substances. In most cases, liquids are considered to be incompressible and gases are considered to be compressible. But there are exceptions in some everyday engineering applications, and they can easily be explored using mathematical modeling.

Engineers also use special mathematical equations to determine certain characteristics of fluid flow, such as whether the flow is slow and smooth (laminar) or turbulent. For example, the ratio of inertia forces to viscous forces within a fluid can be expressed by what is called the Reynold’s number; laminar fluid flow can be described by the Navier-Stokes equations. For no viscosity (or an ideal flow called inviscid flow), the Bernoulli equation can be used. Finally, when the flow is zero (or static), the fluid is governed by the laws and equations of fluid statics.

How old is the study of fluid mechanics?

According to many historians, fluid mechanics may be the oldest subfield in physics and engineering. In particular, ancient civilizations needed to control water flow for agricultural development, drinking-water supplies, and transportation. Thus, the development of fluid mechanics, which is the study of the motion and behavior of fluids, led to even more (and complex) improvements. For example, agricultural requirements led to irrigation waterways, dams, weirs, pumps, and even crude forms of “sprinkler systems”; the need for a potable (drinkable) water supply led to better wells, fountains, and water storage systems; and water transportation innovations included improved sails and rigs, as well as methods to build and waterproof sailing vessels.

To understand the way lava flows from a volcano, mathematicians apply their knowledge of fluid mechanics.

But early fluid mechanical studies did not end there. Over time, they extended into almost every realm of science and engineering. For example, mechanical engineering uses fluid mechanics because of the need to know about fluids used in combustion (ships and automobiles), lubrication (from the smaller inner workings of a wheel to larger mechanisms such as locks along a canal), and energy systems (hydroelectric power). Civil engineering utilizes fluid mechanical studies to interpret how fluid systems traveled over structures (aqueducts and pipes carrying drinking or waste water). Electrical engineers use fluid flow to analyze how to cool electronic devices with either air or water. Even early (and current) aeronautical engineers needed to know how air flowed over an airplane wing, providing the much-needed lift that allows a plane to become airborne.

How are studies of fluid mechanics used today?

The list of engineering uses of fluid mechanics in the modern world seems endless— and no wonder, since it is one of the most widely applied areas of mathematics and engineering. Some of today’s uses of fluid mechanics in various fields include: understanding the movement of molten (liquid) rock, or lava, in volcanic eruptions; studying the flow of air over objects to help design airplanes, the space shuttle, and even spacecraft that fly through the atmospheres of other planets; air flow studies in the automobile industry to design cars with more aerodynamic profiles; analyzing the ups and downs of the stock market; examining natural hazards, such as snow conditions that result in an avalanche; interpreting turbulent flow in sewer and water pipes, and in river channels; studying complicated flow of weather patterns in the atmosphere; researching the effects of gravity (and other) waves in space; and using fluid mechanics applications to study the deep oceans and coastal shorelines, including waves and currents.

CIVIL ENGINEERING
AND MATHEMATICS

How do civil engineers use mathematics?

Although most civil engineers actually spend only a small portion of their time doing calculations, mathematics is essential to this field. For example, civil engineers may use math to carry out the technical calculations in order to plan a construction project. They may use math to model and simulate the possible behavior of a structure before it is actually built. They also use math to understand the necessary chemistry (the strength of a material) and/or physical components (how strong parts need to be) of a construction project.

How do surveyors use mathematics?

Surveyors use mathematics—especially geometry and trigonometry—because they need to measure angles and distances on the ground. They then interpret the data, accurately plotting such information as boundaries and locations of structures on a map. These maps are then used for personal or legal means, such as a survey of a person’s lot showing ownership boundaries in order to obtain a mortgage. The traditional method of surveying is called plane surveying, which does not take into consideration the curvature of the Earth because, for most small projects, this curvature doesn’t really matter. When it does, especially for projects measuring greater distances, the method used is called geodetic surveying.

Geometry and trigonometry are essential mathematical disciplines that surveyors must understand to measure property boundaries accurately.

How do surveyors make measurements?

Most of a surveyor’s measurements are gathered with a theodolite, an instrument that acts as a telescope, ruler, and protractor. The theodolite is set up over a known spot, such as a previously surveyed corner of a lot; its telescope then sights a specific spot, such as another corner of a lot, and the distance is measured (most modern theodolites use lasers to measure distance), supplemented by angular measurements in both the horizontal and vertical planes. The surveyor then uses trigonometry to analyze the data, converting it to a more usable form, usually in x, y, and z coordinates. For example, depending on the desired outcome, the vertical angle and slope distances can be converted from polar measurements to show differences in elevations and horizontal distances. The horizontal distances and angles can also be converted from polar measurements to rectangular coordinates. (For more about coordinates, see “Geometry and Trigonometry.”)

How is linear algebra used to determine the stability of structures?

Structural engineers use linear algebra a great deal, mainly because there are numerous equations with many unknowns associated with the analysis of a structure in equilibrium. Most of the time, these equations are linear, even when bending (material deformation) is involved. Linear algebra can also be used for other structural concerns, because it deals with the study of vectors, vector spaces, linear transformations, and systems of linear equations. Of course, linear algebra is not only used to understand structures; almost every subfield in engineering uses these types of mathematical calculations. (For more about linear algebra and linear equations, see “Algebra.”)

How is math used to calculate the pressure behind a dam?

There are many engineering considerations and calculations needed when building a dam, the most important being the water pressure behind the structure. Engineers know that as the elevation of water behind a dam increases, the height and density of the water causes higher pressures at the bottom of the dam. Thinking in mathematical terms, the horizontal force acting on the dam is the integral of the water pressure over the area of the dam that is in contact with the water. The force exerted by the water pushes horizontally on the dam face, and this is resisted by the force of static friction between the dam and the bedrock foundation on which it rests. The water also tries to rotate the dam about a line running along the base of the dam; the torque resulting from the weight of the dam acts in the opposite sense.

Hoover Dam, an impressive structure on the Colorado River, could only have been made possible by engineers designing it in such a way that the walls were thick enough to withstand massive water pressure.

For example, take the water pressure on a dam, such as the Hoover Dam on the Colorado River between Arizona and Nevada. Before building that dam, engineers needed to know the pressure not only along the entire structure, but also—and especially—at its base. In general, the pressure exerted by water equals the density times the depth, in which the density of water is 62.4 pounds per cubic foot. For Hoover Dam, this gives a pressure of 37,440 pounds per square foot, or 18.72 tons per square foot; the pressure calculated at half the height of the dam is 9.36 tons per square foot. This is why the base width of the dam is 1,660 feet (201.2 meters)—it is thicker to compensate for the increase in pressure at the bottom of the dam—while the width of the crest of the dam is only 45 feet (13.7 meters).

How is mathematics used to enable buildings to withstand earthquakes?

It is not usually the quake that kills people, but the collapse of structures. In particular, the horizontal shaking during a quake is mostly responsible for causing building or road damage and collapse. Most structures are designed to carry heavy loads, so they are strong in the vertical direction. Designing structures to withstand the horizontal earthquake shaking can save buildings and lives.

There may be other ways to mitigate the amount of structural collapse during quakes that include a healthy dose of simple and complex mathematics. One expensive way would be to design all buildings to withstand the largest ground shaking an area could expect. This could be done using mathematics familiar to designers and engineers; the math involved analyzes how large quake frequency waves travel through and area. Yet another, more practical, solution might be to design buildings to withstand the specific types of shaking expected in a region (this could be based on the rock underneath; earthquake waves travel differently in sand and rock). Again, mathematics could be used to determine the frequency at which each building vibrates (or the number of times a building sways per second) versus the potential type of quakes that roll through the area.

MATHEMATICS AND ARCHITECTURE

What is architecture?

Simply put, architecture is the design of structures, mainly buildings, by architects. But the definition does not end there. An architect not only builds the structures, he or she also takes into consideration the form, symmetry, spaces, and beauty of the building. In order to do this, mathematics is needed to work out such building factors as angles, distances, shapes, and sizes.

How has math been used historically in architecture?

Historically, there has been a great connection between architecture and mathematics. Ancient mathematicians were architects and vice versa, using their skills to build pyramids, temples, aqueducts, cathedrals, and a range of other architectural structures we find beautiful and awesome today. For example, in ancient Greece and Rome, architects were required to also be mathematicians. During medieval times, most buildings and structures carried some symbolic reference to the church; the mathematical end of architecture was almost forgotten during this time. By the European Renaissance around 1400, a new kind of architecture developed that emphasized mass and interior space to produce aesthetically pleasing “pictures” similar to those found in paintings and sculptures. This led to an entirely new way of looking at architecture and altered its connection to mathematics.

The Akashi-Kaikyo Bridge in Japan is the world’s longest suspension bridge, stretching almost 13,000 feet across the Akashi Strait near Kobe. Careful engineering was needed to make the bridge stable not only on routine days, but also in case of days when there are earthquakes in the geologically active region.

Who was Vitruvius?

Marcus Vitruvius Pollio (c. first century B.C.E.) was a Roman writer, architect, and engineer. He was the author of De Architectura libri decem, known today as The Ten Books of Architecture. This Latin treatise, dedicated to Octavian, the heir and adopted son of Julius caesar, was written around 27 B.C.E. (For more about Octavian, see “Mathematics throughout History.”)

What is the world’s longest suspension bridge?

Ten years after construction began, Japan’s Akashi-Kaikyo Bridge—also known as the Pearl Bridge—was finally opened on April 5, 1998. At this writing, it still holds the title as the longest suspension bridge in the world, stretching 12,828 feet (3,910 meters) across the Akashi Strait to link the city of Kobe with Awaji-shima Island. Its main span length (or center section, which is the way “world’s longest” status is determined) reaches 6,532 feet (1,991 meters) between support columns. The span length is almost a quarter mile longer than the previous record holder, the StoreBaelt (Great Belt East Bridge) in Denmark, which also opened in 1998.

But this bridge may eventually lose its longest status if the Italian government can keep on track with building the estimated 1.3 billion Euro bridge called the Strait of Messina Bridge, stretching between mainland Italy and Sicily. The idea for such a bridge has been around since Roman times. Fast-forward to modern times, and the idea for the bridge was backed by the government in 2001; with money tight, it was scrapped in 2006. As of this writing, it has been revived again; if it is built, it will be the longest suspension bridge in the world, spanning over the strait that connects the Ionian Sea in the south to the Tyrrhenian Sea to the north. It will be quite an engineering feat, with the main span reaching just over 10,827 feet (3,300 meters), which is almost double the main span of the Akashi-Kaikyo.

Interestingly enough, Japan and Italy are known to be tectonically active, with both receiving their fair share of volcanic eruptions and earthquakes, as well as, in Japan, tsunamis (seismic waves that form in the oceans and can be tens of feet high; for more about tsunamis, see “Math in the Natural Sciences”).

Possibly the first works published about architecture, the books entailed a compilation of architectural ideas of Vitruvius’s day and covered the following ten subjects: principles of architecture; history of architecture and architectural materials; Ionic temples; Doric and Corinthian temples; public buildings, theaters, music, baths, and harbors; town and country houses; interior decoration; water supply; dials and clocks; and mechanical engineering with military applications. Specifically, the topics included such forward-thinking ideas as the manufacture of building materials and dyes (material science), machines for heating water for public baths (chemical engineering), amplification in amphitheaters (acoustical engineering), and the design of roads and bridges (civil engineering).

De architectura was wildly successful, and Vitruvius’s architectural advice was followed for centuries. But because Vitruvius’s books were passed down through the ages, they were copied by various people, especially throughout the Middle Ages. Many medieval engineers added information to the texts, treating the books as handbooks, not documents to be preserved. In the end, historians have had to winnow away the added sections to find the true writings of Vitruvius.

What is the golden ratio?

The golden ratio (also known as extreme and mean ratio, golden section, golden mean, or divine proportion) is a number that has many interesting properties; it is associated with the balance between symmetry and asymmetry used in art and design. Two quantities are said to be in the golden ratio if the “whole is to the larger as the larger is to the smaller.” Euclid expressed it as, “A straight line is said to have been cut in extreme and mean ratio when, as the whole line is to the greater segment, so is the greater to the less.” This is seen in the accompanying illustration, in which for two segments “a” and “b,” the entire line is to the “a” segment as “a” is to the “b” segment.

The symbol for the golden ratio is φ (the Greek letter “phi,” or a circle with a vertical slash through it); it is equal to about 1.6103398 and is considered an irrational number. The calculation to reach the golden ratio is as follows:

This equals the quadratic equation:

which results in:

What is the historical significance of the golden ratio?

It is thought that over the centuries many architects and painters used it in their works. Some historians believe that the Great Pyramid of Cheops contains the golden ratio. The ancient Greeks knew about the golden ratio from their works in geometry, but they never truly believed it was as important as numbers such as pi (π). Many works of art in the Renaissance are thought to have used the golden ratio within paintings and sculptures, although it may have been subconsciously incorporated into their compositions. In 1509 Luca Pacioli published the work Divina Proportione, which explored the mathematics of the golden ratio, along with its use in architectural design.

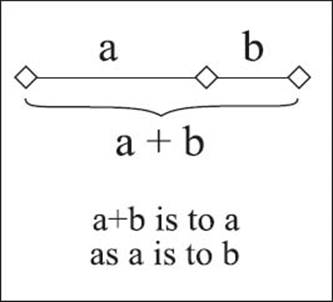
The idea of the golden ratio is illustrated here by the relationships between a, b, and a + b.

Of course, humans aren’t the only ones who “practice” the golden ratio. It is also seen in nature as the result of the dynamics of some systems. For example, the spacing of sunflower seeds—and even the shape of the chambered nautilus shell—are all often claimed to be related to the golden ratio.

Cutting a nautilus shell in half reveals chambers that follow the rules of the golden ratio. It is a beautiful example of how math can be found all around us in nature.

In what way do some historians link mathematics to the pyramids?

The pyramids in Egypt were built as royal tombs for the pharaohs—first along the edges of cliffs as low rectangular structures called mastabas, then as tall, four-sided pyramids. The three structures most of us associate with pyramids were built at Giza, near Cairo, about 2500 B.C.E. The largest of these, the great pyramid of the pharaoh Cheops, measures 481 feet (147 meters) high. But there are no intricate pathways in this pyramid; it is merely a pile of limestone blocks weighing between 3 and 15 tons.

Why did the Egyptians choose the pyramid form? Historians know that the Egyptian Sun god, with its rays reaching for the Sun, was represented by pyramid-shaped stones, or ben-bens. And because the Egyptians worshipped the Sun as their chief god, the pyramids are thought to be huge renditions of the ben-bens. After a pharaoh died, the pyramids would be symbolic of the pharaoh ascending the Sun’s rays to join his Sun god.

Some historians also believe that the pyramids may have had some (still hidden) numerical significance. In particular, some believe the ratio of the pyramid’s perimeter to its height times two, or P/(2 × H), gives a close approximation to the value of pi (π); another claim is that the slopes of the pyramids’ sides were also expressions of pi.

What was the original use of Stonehenge?

One of the most famous ancient stone complexes is England’s Stonehenge, an impressive engineering and mathematical feat. Several groups of local inhabitants constructed this collection of large and small stones grouped in four concentric circles—two of which are created by paired upright stones bearing huge capstones—between 2950 and 1600 B.C.E. Based on how the stones line up with various astronomical events, historians believe the entire structure represents a huge (literally monumental) calendar. For example, various stones align with the Moon (the full moon’s extreme positions on the horizon are marked at Stonehenge) and with the Sun (including the summer solstice). It is also thought that the complex served as a place in which ancient rites and rituals were performed on significant days of the year. And it was all built without the help of computers.

The famous ancient structure of Stonehenge in England is now believed to have been designed to measure astronomical events as part of a religious tradition.

What are the modern connections between architecture and mathematics?

The foundations of modern architecture began with mathematics. Mathematical planning goes into creating almost every working, free-standing structure, from the smallest monument to the tallest buildings and bridges. For example, in order to build a structure, the area where the building will be erected must be measured to see if it will fit (measurements and surveys); then the building plans need to be drawn up in scale drawings made proportionally smaller to the structure’s real size (for more information, see below); and the amount of building material must be estimated (mathematics to figure out the budget). Finally, the actual structure must be built to specifications so the building will stand without collapsing (geometry and measurement).

What famous structures were built using mathematics?

Actually, all famous structures needed mathematics, especially in the initial phases of design and construction. Some of the more famous—and exceptionally challenging— buildings include the Chrysler Building in New York (a steel frame skyscraper built around 1930 that was the tallest building in the world before the Empire State Building); the Empire State Building in New York (a steel-framed, stone-clad commercial office skyscraper built in 1931 that rises 1,252 feet [381 meters] high); the Eiffel Tower in Paris, France (designed by architect Gustave Eiffel and built between 1887 and 1889 as a 985-foot-[300-meter-] tall exposition iron observation tower); and the Sears Tower in Chicago (built between 1974 to 1976, it is a steel-frame with glass structure standing at 1,450 feet [442 meters] tall and is, to date, the tallest building in the United States). Places such as the Monterey Aquarium (built around 1980 with reinforced concrete and made compatible with surrounding waterfront structures) also needed mathematics in order to be constructed. Of course, when one gets down to it, all types of construction require some math knowledge for them to be built, even a modest piece of cabinetry.

Gustave Eiffel used mathematical concepts to design his famous Eiffel Tower in France between 1887 and 1889.

What are scale drawings?

Scale drawings are drawings or illustrations that are proportional in scale to the real structures they represent. In order for a new building to be designed, an architect must convert his or her ideas to drawings. But since the drawings can’t be as large as the building, the architect uses scale drawings to depict the structure. These miniature versions of the actual structure show the sizes, shapes, and arrangements of rooms, along with structural parts, windows, doors, closets, and other important details of construction. The scale drawings of these buildings must be in exact proportion to the actual structure, with various scales used for this purpose. For example, 1/8 inch might be used to represent one foot; thus, an eight-foot-long building feature would be drawn as an inch long on paper. One of the most common scales used by architects is ¼ inch = 1 foot. (These measurements can also be translated into the metric scale.)

Scale drawings are also used in other engineering fields, such as surveying. For example, distances measured in the field can be translated to a smaller scale (such as a drawing) in order to accurately depict what was measured. The ratio between the real distance and the drawn distance is called the drawing scale. If the measurement is 200 feet in the field, and on paper the desired line is 8 inches long, then 8 inches on the paper would equal 200 feet on the ground, and 1 inch would be equal to 25 feet on the ground. This is translated as a diagram with a scale of 1” = 25’ (1 inch equals 25 feet), or 1:25. There is another way of approaching such an illustration: If the longest distance measured in the field was 300 feet and the desired drawing scale is 1 inch = 25 feet, then the minimum length of paper needed would be 12 inches, or 300/25.

The patterns on a butterfly’s wings demonstrate the concept of symmetry in nature.

How are the principles of ratio, proportion, and symmetry applied to architecture?

The definition of a ratio is a comparison by division of two quantities expressed as the same unit measurement. For example, a building that is 200 feet wide and 100 feet tall has a ratio of 2:1 (200:100) between its width and height; it is also seen as the fraction ½. Such a relationship was understood as far back as ancient Greece and Rome, when people used mathematics to give structure and aesthetics to buildings. This is especially important in architecture, in which building design is based on complex mathematical ratios.

Proportion is an equation stating that two ratios are equal. Every proportion has four terms, with the first and fourth terms being the extremes; the second and third terms are called the means. In each proportion, the product of the means equals the product of the extremes. The Greeks and Romans often used proportions in their buildings and other structural designs. (The Roman architect Vitruvius was also instrumental in praising the virtues of proportion and symmetry in architecture; for more about Vitruvius, see above.) During the Renaissance, architects applied proportion (and other mathematical formulas) to produce aesthetically pleasing buildings— beauty that still holds true today.

Although there are other types of symmetry, the most common is line symmetry, in which a line divides an object, line, or other structure into two equal halves (an example in nature would be the wings of a butterfly). If a line of symmetry is drawn, each point on one side of the line has a corresponding point on the opposite side of the line. If you connect these two points, the line is perpendicular to the line of symmetry. There is a more mathematical way of defining symmetry: Two points are symmetric about a line if the line is the perpendicular bisector of the segment joining the two points. Symmetry was used by ancient (and modern) architects to maintain visual and sometimes structural balance of a building or structure.

ELECTRICAL ENGINEERING
AND MATERIALS SCIENCE

How is mathematics important to electrical engineering?

There are many branches of mathematics that are important to electrical engineering. For example, abstract math is used in communication and signal processing. Complex differential equations—solving equations involving derivatives—are used in circuit theory and systems design; also in circuit theory, engineers need to know algebra and trigonometry. Engineers who deal with electromagnetism need to know calculus, especially Maxwell’s equations. (For more about Maxwell, see “Math in the Physical Sciences.”)

How are imaginary numbers used in electrical engineering?

Imaginary numbers are used in electrical engineering because complex numbers are an integral part of electrical problems. In fact, there are often more imaginary numbers in electrical engineering problems than there are real numbers. This is because a complex number is a pair of numbers in which one number is real, the other imaginary (or a real number multiplied by the value i, defined as the square root of -1; for more information about imaginary numbers, see “Math Basics”).

For instance, we know electricity flows through an electrical circuit component such as a light bulb. The bulb actually resists the flow of some electricity by doing work—or shining—thus, the current is real and measured by a current meter. But if the current can’t flow through a device, the current becomes imaginary. For example, a capacitor is two pieces of metal that do not touch; therefore, if one adds a voltage, no real current can flow through it.

How is mathematics used to
determine resistor values in an electrical network?

Electrical engineers who deal with systems and circuit theory need to know the terms and functions of the basic circuit element—resistor, capacitor, and inductor—in terms of current-voltage associations determined by impedance (obstruction). Complex numbers, calculus, and Laplace transforms (see above) are all mathematical concepts used to understand circuit theory.

The best way to understand the basics are through the following simple equations:

Resistor—Voltage = current (I) times resistance (R), or V = IR.

Capacitor—Voltage = the square root of -1 (j, often called i, or an imaginary number) times frequency (w) times the capacitance (C)—all times the current (I), or V = (jwC)I;

Inductor—Voltage = the current divided by the square root of -1 (j), times frequency (w), times inductance (L), or V = I/(jwL).

Is math used to describe the strength of materials?

Materials science is also a major part of engineering, and includes a great deal of mathematics. For example, engineers need to know how materials stand up to stress and strain from the pressure of either a structure or overlying materials. A basic understanding of how structures respond to the action of forces and how these forces affect the performance of various building materials, such as wood, steel, concrete, and so on, is essential.

Are advances in technology fundamental to our understanding of materials?

Yes, advances in technology are truly fundamental to our understanding of materials, and vice versa. For example, transistors and superconductors were developed by understanding the mathematics of the materials that make up these objects. Math and materials science together have also advanced technology used in infrastructure (such as highways and overpasses), aerospace (such as satellites and shuttles), and micro-electronics (such as those found in automobiles). Today, the need to describe material behavior resulting from physical interactions is forcing scientists to develop new mathematics. In fact, materials science has evolved to the point in which researchers from physics, engineering, and applied mathematics are working together on common problems.

CHEMICAL ENGINEERING

How is mathematics used in chemical engineering?

Mathematics is used a great deal in chemical engineering, especially since chemical engineers design materials and the processes by which those materials are made. To solve chemical problems, many types of mathematics are used, not least of which is calculus (including partial differential equations). Even simple calculations, such as working on chemical formulas and equations, involve mathematics. (For more information about chemical formulas and equations, see “Math in the Physical Sciences.”)

Traditionally, chemical engineers worked in the petroleum and large-scale chemical industries. More recently, they have spread out to the pharmaceutical, foodstuff, polymer and material, microelectronics, and biotechnology industries. Using mathematics, they are involved in such studies as thermodynamics, chemical reaction processes, and process dynamics, design, and control. They help to develop new chemical products and processes, test processing equipment and instrumentation, gather data, and monitor quality.

Chemical engineers also build mathematical models and analyze the results, mostly to help understand the performance of a process. In fact, the “solution” to a math problem is often in the understanding of the behavior of the process described by the mathematics, rather than the specific numerical result.

What are some examples of mathematical models used by chemical engineers?

There are numerous examples of how mathematical models are used by chemical engineers—too many to mention them all here. One good example is modeling crystal growth: Liquids—from water to molten metals—become crystalline solids as they are cooled. Engineers can mathematically design software that helps in the manufacture of superior crystalline growth, especially for electronics and other industries. These improved crystal forms advance the quality of electronic hardware, including computers, and help engineers design better alloys for a wide range of applications.

How is math used to understand chemical reactions?

One of the simplest examples of mathematics used in understanding chemical reactions is based on two chemicals, A and B (they can be molecules or ions). If A and B encounter one another, they can rearrange themselves into molecules or ions of two other substances: in this example, C and D. The reaction that takes place can give off or absorb energy, making the molecules move faster or slower. Although this is a simple example of what can happen in a chemical reaction, it can still be analyzed using mathematical modeling. For example, given starting amounts of A, B, C, and D molecules at time t = 0, what would the molecules be like at time t₁ (or after a specific amount of time)? These and more complex chemical engineering questions can be answered using mathematical modeling.

INDUSTRIAL AND
AERONAUTICAL ENGINEERING

How are statistics used in industrial engineering?

Industrial engineers study the efficient use of personnel, materials, and machines in factories, stores, repair shops, and offices. They prepare layouts of machinery and equipment, plan the flow of work, make statistical studies, and analyze production costs. In particular, they rely heavily on a branch of mathematics called statistics and probability. (For more about statistics and probability, see “Applied Mathematics.”)

How is math used in statistical process control?

Statistical process control (SPC) involves using statistical techniques to measure and analyze the variations within a process. With SPC, industrial engineers monitor, control, and, ideally, improve a process through statistical analysis. The four basic steps include measuring the process, eliminating variables within the process to make it consistent, monitoring the process, and, finally, improving the process to make the (usually better) intended product. But it is not the answer to everything. All the SPC does is ensure that the product is being manufactured and designed as intended. Thus, SPC does not tell whether the design is good or bad, just if it’s made according to plan.

What is reliability?

Industrial engineers use another type of statistical technique called reliability, a system that always produces the same results and that hopefully meets or exceeds its specifications. A product is analyzed using the reliability function (or survivor function): the probability of a unit in a system that does not fail in a certain specified time interval. If the unit does fail in a system, it means the end of the unit’s ability to perform the required function. This is determined by the failure distribution function, or the probability of an item failing in a specific time interval.

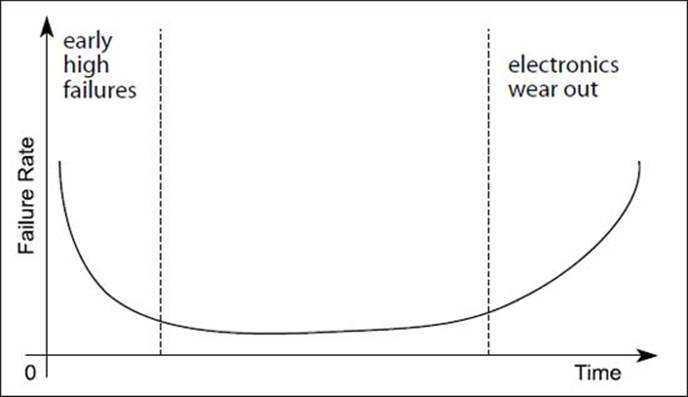
Calculations involving the common failure rates of various mechanical devices often results in a graph with a bathtub-shaped curve.

What is statistical quality control?

Quality control has been around for a while in a crude sense. When a certain product was manufactured, and consumers chose that product, the makers would try to improve the quality of the product or lower its price. The improvement of the quality did not stop with the product, but also included the process for making the product. But the use of mathematics was minor in early quality control. It was not until the 1920s that statistics was applied to industry and quality control, mainly because of the development of sampling theory. (For more about sampling, see “Applied Mathematics.”)

Modern statistical quality control refers to using statistical techniques for measuring and improving the quality of processes; it is often broken down into statistical process control (SPC, see above) and statistical quality control (SQC). Both terms are usually used interchangeably, although SQC has a broader focus than SPc. To compare, SPC is the application of statistical techniques to control a process, reducing variation so that performance remains within specific limits; SQC is the application of statistical techniques to control quality and includes acceptance sampling (inspection of a sample from a lot to decide whether to accept that lot) as well as SPC.

What is the bathtub curve?

Industrial engineers usually know about the bathtub curve, especially in reference to an operating or failing unit. In other words, if enough units from a given population are observed operating and failing over time, it is relatively easy to compute week-by-week (or month-by-month or year-by-year) estimates of the failure rate. The results of the calculated population failure rates over time produces a graph. Because the shape of this failure rate curve resembles the end-to-end section of an antique bathtub, it is widely known as the “bathtub curve.” This type of analysis is usually used in industrial settings. For example, it can describe the expected failure rate of certain electronics over time: initially high; then dropping to 0 failures for most of the system’s lifetime; then rising again to the other end of the “tub” as the electronics “tire out.”

What is an aerospace engineer?

Aerospace engineers are directly involved with putting objects—from airplanes and the space shuttle to deep-space craft—into the sky and beyond. Using sundry mathematical models and techniques, they install, construct, maintain, and test systems used to launch, diagnose, or track aircraft and space vehicles. They may calibrate test equipment and determine causes of equipment malfunctions. Using computers and communications systems, aerospace engineers often record and interpret test data.

What is orbital mechanics?

Orbital mechanics, also called flight mechanics, is the study of the motions of artificial satellites and space vehicles moving under the influence of forces such as gravity, atmospheric drag, thrust, and so on. It is a modern spin-off of celestial mechanics, or the study of the motions of planetary and celestial bodies. One of the main scientists who built the foundations of orbital mechanics was mathematician Isaac Newton (1642–1727), who put forth his laws of motion and formulated the law of universal gravitation. (For more about Newton, see “History of Mathematics” and “Mathematical Analysis”; for more about Newton’s laws, see “Mathematics in the Physical Sciences.”) Today’s aerospace engineers apply orbital mechanics to such problems as rocket and spacecraft trajectories, reentry and landing of space vehicles, rendezvous computations (such spacecraft to the International Space Station), and lunar and interplanetary trajectories for unmanned vehicles.

Without knowing the mathematics involved in orbital mechanics, the International Space Station would plunge back into the Earth instead of circling it in a stable orbit.

How do engineers determine the escape velocity of a rocket?

A ball thrown into the air will rise and then return, thanks to the Earth’s gravity. If the ball is given a larger initial velocity, it will rise even higher and then return. With even more velocity, the ball will reach a certain escape velocity, in which the ball “escapes” the gravitational pull of the planet. If the ball is launched with an initial velocity greater than the escape velocity, it will rise and not return. In this case, physicists say that the ball was given enough kinetic energy to overcome all of the negative gravitational potential energy—or, it launches into space. Thus, if m is the mass of the ball, M is the mass of the Earth, G is the gravitational constant, v is the velocity, and R is the radius of the Earth, then the potential energy is equal to GmM/R. The kinetic energy of the launched ball is equal to mv2/2. That means the escape velocity is equal to:

This is independent of the mass of the ball. To see how this works to an aerospace engineer, just replace the word “ball” with “space vehicle.”

How is mathematics used in the SETI program?

Although as of this writing the SETI (Search for Extraterrestrial Intelligence) program has had funding problems, its use of mathematics in seeking intelligent life on other planets has always been fascinating. Large computers at several facilities, including the University of California at Berkeley, analyze data from various radio telescopes in real time (including at Arecibo in Puerto Rico), seeking out data that could be indicative of an alien civilization. Because of the large number of personal computers currently in use around the globe, SETI researchers have enlisted help from the public to seek out new civilizations. A program can be downloaded to private computers and used to run data in the background while the computer user works on other programs; the results are then automatically transmitted to SETI researchers.

Overall, a computer program looks at a large slice of the electromagnetic spectrum—a band 100 MHz (megahertz) centered around 1420 MHz. (It does this by performing a variety of digital signal processing operations on radio frequency data, translating the information using a special algorithm.) This part of the spectrum is where scientists predict an “advanced civilization” would most likely be sending out a signal, concentrating the message’s power in one narrow frequency range, and if the signal strength gets higher that might be evidence of an extrasolar civilization.