The Handy Math Answer Book, Second Edition (2012)

THE HISTORY OF MATHEMATICS

WHAT IS MATHEMATICS?

What is the origin of the word “mathematics”?

According to most sources, the word mathematics is derived from the Latin mathmaticus and from the Greek mathematikos, meaning mathematical. (Other forms include mathema, meaning “learning,” and manthanein, meaning “to learn”.)

In simple terms, what is mathematics?

Mathematics is often referred to as the science of quantity. The two traditional branches of mathematics have been arithmetic and geometry, using the quantities of numbers and shapes. And although arithmetic and geometry are still of major importance, modern mathematics expands the field into more complex branches by using a greater variety of quantities.

Who were the first humans to use simple forms of mathematics?

No one really knows who first used simple forms of mathematics. It is thought that the earliest peoples used something resembling mathematics by knowing the concepts of one, two, or many. Perhaps they even counted using items in nature, such as 1 represented by the Sun or Moon; 2, their eyes or wings of a bird; clover for 3; or legs of a fox for 4.

Archeologists have also found evidence of a crude form of mathematics in the tallying systems in certain ancient populations. These include notches in wooden sticks or bones, and piles or lines of shells, sticks, or pebbles. This is an indication that certain prehistoric peoples had at least a simple, visual ways of adding and subtracting things, but they did not yet have a numbering system such as we have today.

EARLY COUNTING AND NUMBERS

What are some examples of how early peoples counted?

There were several different ways that early civilizations recorded the numbers of things. Some of the earliest archeological evidence of counting dates from about 35000 to 20000 B.C.E., in which several bones bear regularly-spaced notches. Most of these marked bones have been found in Western Europe, including the Czech Republic and France. The purpose of the notches is unclear, but most scientists believe they do represent some method of counting. The marks may represent an early hunter’s number of kills; a way of keeping track of inventory (such as sheep or weapons); or a way to track the movement of the Sun, Moon, or stars across the sky as a kind of crude calendar.

Not as far back in time, shepherds in certain parts of West Africa counted their flock by using shells and various colored straps. As each sheep passed, the shepherd threaded a corresponding shell onto a white strap, until nine shells were reached. As the tenth sheep went by, he would remove the white shells and put one on a blue strap, representing ten. When 10 shells, representing 100 sheep, were on the blue strap, a shell would then be placed on a red strap, a color that represented what we would call the next decimal up. This would continue until the entire flock was counted. This is also a good example of the use of base 10. (For more information about bases, see “Math Basics.”)

Certain cultures also used gestures, such as pointing out parts of the body, to represent numbers. For example, in the former British New Guinea, the Bugilai culture used the following gestures to represent numbers: 1, left hand little finger; 2, next finger; 3, middle finger; 4, index finger; 5, thumb; 6, wrist; 7, elbow; 8, shoulder; 9, left breast; 10, right breast.

An Egyptian calendar on papyrus. Ancient cultures such as that in Egypt developed mathematics for practical purposes, such as for calculating time for planting and harvesting crops.

Another method of counting was accomplished with string or rope. For example, in the early 16th century, the Incas used a complex form of string knots for accounting and sundry other reasons, such as calendars or messages. These recording strings were called quipus, with units represented by knots on the strings. Special officers of the king called quipucamayocs, or “keepers of the knots,” were responsible for making and reading the quipus.

Why did the need for mathematics arise?

The reasons humans developed mathematics are the same reasons we use math in our own modern lives: People needed to count items, keep track of the seasons, understand when to plant. Math may even have developed for religious reasons, such as recording or predicting natural and/or celestial phenomena. For example, in ancient Egypt, flooding of the Nile River would wash away all landmarks and markers. In order to keep track of people’s lands after the floods, a way to measure the Earth had to be invented. The Greeks took many of the Egyptian measurement ideas even further, creating mathematical methods such as algebra and trigonometry.

How did certain ancient cultures count large numbers?

It is not surprising that one of the earliest ways to count was the most obvious: using the hands. And because these “counting machines” were based on five digits on each hand, most invented numbering systems used base 10. Today, we call these base numbers—or base of a number system—the numbers that determine place values. (For more information on base numbers, see “Math Basics.”)

However, not every group chose 10. Some cultures chose the number 12 (or base 12); the Mayans, Aztecs, Basques, and Celts chose base 20, adding the ten digits of the feet. Still others, such as the Sumerians and Babylonians, used base 60 for reasons not yet well understood.

The numbering systems based on 10 (or 12, 20, or 60) started when people needed to represent large numbers using the smallest set of symbols. In order to do this, one particular set would be given a special role. A regular sequence of numbers would then be related to the chosen set. One can think of this as steps to various floors of a building, in which the steps are the various numbers—the steps to the first floor the “first order units”; the steps to the second floor the “second order units”; and so on. In today’s most common unit (base 10), the first order units are the numbers 1 through 9, the second order units are 10 through 19, and so on.

What is the connection between counting and mathematics?

Although early counting is usually not considered to be mathematics, mathematics began with counting. Ancient peoples apparently used counting to keep track of sundry items, such as animals or lunar and solar movements. But it was only when agriculture, business, and industry began that the true development of mathematics became a necessity.

What were the two fundamental ideas in the development of numerical symbols?

A numeral is a standard symbol for a number; numerical symbols in various cultures represent numbers. For example, XXII is the numerical symbol—also called a Roman numeral—that corresponds to 22—also a numerical symbol—in the standard Hindu-Arabic numerals. In the Mayan system, a combination of two symbols, a dot (.) and a dash (-), were used to define numbers.

There were two basic principles in the development of numerical symbols: First, a certain standard sign for the unit is repeated over and over, with each sign representing the number of units. For example, III is considered 3 in Roman numerals (see the Greek and Roman mathematics section for more about Roman numerals). In the other principle, each number has its own distinct symbol. For example, “7” is the symbol that represents seven units in the standard Hindu-Arabic numerals. (See below for an explanation of Hindu-Arabic numbers; for more information, see “Math Basics.”)

What are the names of the various base systems?

The base 10 system is often referred to as the decimal system. The base 60 system is called the sexagesimal system. (This should not be confused with the sexadecimal system—also called the hexadecimal system—or the digital system based on powers of 16.) A sexagesimal counting table is used to convert numbers using the 60 system into decimals, such as minutes and seconds.

The following table lists the common bases and corresponding number systems:

MESOPOTAMIAN NUMBERS AND MATHEMATICS

What was the Sumerians’ oral counting system?

The Sumerians—whose origins are debated, but who eventually settled in Mesopotamia—used base 60 in their oral counting method. Because it required the memorization of so many signs, the Sumerians also used base 10 like steps of a ladder between the various orders of magnitude. For example, the numbers followed the sequence 1, 60, 60², 60³, and so on. Each one of the iterations had a specific name, making the numbering system extremely complex.

Who were the Mesopotamians?

The definition of who the Mesopotamians were is not easy because there are many historians who disagree on how to distinguish Mesopotamians from other cultures and ethnic groups. In most texts, the label “Mesopotamians” refers to most of the unrelated peoples who used cuneiform (a way of writing numbers; see below), including the Sumerians, Persians, and so on. They are also often referred to as Babylonians, after Babylon, which was the center of many surrounding empires that occupied the fertile plain between the Tigris and Euphrates Rivers. But this area was also called Mesopotamia. Therefore, the more correct label for these people is probably “Mesopotamians.”

In this text, Mesopotamians will be referred to by their various subdivisions because each brought new ideas to the numbering systems and, eventually, mathematics. This includes the Sumerians, Akkadians, and Babylonians.

No one truly knows why the Sumerians chose such a high base number. Theories range from connections to the number of days in a year, weights and measurements— and even that it was easier to use. Today, this numbering system is still visible in the way we tell time (hours, minutes, seconds) and in our definitions of circular measurements (degrees, minutes, seconds).

How did the Sumerian written counting system change over time?

Around 3200 B.C.E., the Sumerians began a written number system, attaching a special graphical symbol to each of the larger numbers at various intervals (1, 10, 60, 3600, etc.). Because of the rarity of stone, and the difficulty in preserving leather, parchment, or wood, the Sumerians used a material that would not only last, but would be easy to imprint: clay. Each symbol was written on wet clay tablets, then baked in the hot sunlight. This is why many of the tablets are still in existence today.

The Sumerian number system changed over the centuries. By about 3000B.C.E., the Sumerians decided to turn their numbering symbols counterclockwise by 90 degrees. And by the 27th century B.C.E., the Sumerians began to physically write the numbers in a different way, mainly because they changed writing utensils from the old stylus that was cylindrical at one end and pointed at the other to a stylus that was flat. This change in writing utensils, but not the clay, created the need for new symbols.

Who were the Akkadians?

The region of Mesopotamia was once the center of the Sumerian civilization, a culture that flourished before 3500 B.C.E. Not only did the Sumerians have a counting and writing system, but they were also progressive, supporting irrigation systems, a legal system, and even a crude postal service. By about 2300 B.C.E., the Akkadians invaded the area, emerging as the dominant culture. As most conquerors do, they imposed their own language on the area and even used the Sumerians’ cuneiform system to spread their language and traditions to the conquered culture.

Although the Akkadians brought a more or less advanced culture into the mix, they were responsible for inventing the abacus, an ancient counting tool. By 2150 B.C.E., the Sumerians had had enough: They revolted against Akkadian rule, and overthrew their conquerers.

However, the Sumerians did not maintain their independence for long. By 2000 B.C.E., their empire collapsed, undermined by attacks from the west by Amorites and from the east by Elamites. As the Sumerians disappeared, they were replaced by the Assyro-Babylonians, who eventually established their capital at Babylon.

The new way of writing numbers was called cuneiform script, from the Latin cuneus, meaning “a wedge” and -formis, meaning “like.”

Did any cultures use more than one base number in their numbering system?

Certain cultures may have used a particular base as their dominant numbering system, such as the Sumerians’ base 60, but that doesn’t mean they didn’t also use other base numbers. For example, the Sumerians, Assyrians, and Babylonians used base 12, mostly in their measurements. In addition, the Mesopotamian day was broken into 12 equal parts; they also divided the circle, ecliptic, and zodiac into 12 sections of 30 degrees each.

What was the Babylonian numbering system?

The Babylonians were one of the first to use a positional system within their numbering system—the value of a sign depends on the position it occupies in a string of signs. Neither the Sumerians nor the Akkadians used this system. The Babylonians also divided the day into 24 hours, an hour into 60 minutes, and a minute into 60 seconds, a way of telling time that has existed for the past 4,000 years. The way we write hours, minutes, and seconds is as follows: 6h, 20”, 15’; the way the Babylonians wrote the same numbers (as sexagesimal fractions) is: 6 20/60 15/3600.

What is the rule of position?

We are most familiar with the rule of position, or place value, as it is applied to the Hindu-Arabic numerals 1, 2, 3, 4, 5, 6, 7, 8, 9, and 0. This is because their value depends on the place or position they occupy in a written numerical expression. For example, the number 5 represents 5 units, 50 is 5 tens, 500 is 5 hundreds, and so on. The values of the 5s depends upon their position in the numerical expression. It is thought that the Chinese, Indian, Mayan, and Mesopotamian (Babylonian) cultures were the first to develop this concept of place value.

The Babylonians left behind impressive artifacts and also advances in mathematics. They were the first civilization to create a positional system for numbers.

Were there any problems with the Babylonian numbering system?

Yes. One in particular was the use of numbers that looked essentially the same. The Babylonians conquered this problem by making sure the character spacing was different for these numbers. This ended the confusion, but only as long as the scribes writing the characters bothered to leave the spaces.

Another problem with the early Babylonian numbering system was not having a number to represent zero. The concept of zero in a numbering system did not exist at that time. And with their sophistication, it is strange that the early Babylonians never invented a symbol like zero to put into the empty positions in their numbering system. The lack of this important placeholder no doubt hampered early Babylonian astronomers and mathematicians from working out certain calculations.

Did the Babylonians finally use a symbol to indicate an empty space in their numbers?

Yes, but it took centuries. In the meantime, scribes would not use a symbol representing an empty space in a text, but would use phrases such as “the grain is finished” at the end of a computation that indicated a zero. Apparently, the Babylonians did comprehend the concepts of void and nothing, but they did not consider them to be synonymous.

Around 400 B.C.E., the Babylonians finally began to record an empty space in their numbers, which were still represented in cuneiform. Interestingly, they did not seem to view this space as a number—what we would call zero today—but merely as a placeholder.

What happened to the Babylonians?

After the Amorites (a Semitic people) founded Babylon, there were several dynasties that ruled the area, including those associated with the famous king and law-maker, Hammurabi (1792-1750 B.C.E.). It was periodically taken over, including in 1594 B.C.E. by the Kassites and in the 12th century B.C.E.by the Assyrians. Through all the conquests, most of the Babylonian culture retained its own distinctiveness. With the fall of the Assyrian Empire in 612 B.C.E., the Babylonian culture bloomed, at least until its conquest by Cyris of Persia in 539 B.C.E. It eventually died out a short time after being conquered by Alexander the Great (356-323 B.C.E.) in 331 B.C.E. (ironically, Alexander died in Babylon, unable to recover from a fever he contracted).

Who were the first to invent a symbol for zero?

Many cultures, including the Chinese and Babylonians, used an empty space as a placeholder, but when “0” comes to be understood as and number and not just a placeholder is still highly debated. Archeologists have found clay tables with three hooks to denote an empty space—from the 8th century B.C.E.—in an ancient Mesopotamian city east of Babylon. The Babylonians used two wedge symbols in the place we would call zero around 400 B.C.E.

Many archeologists believe that a crude symbol for zero was invented either in Indochina or India about the 7th century, a “goose egg” similar to the one we use today. Other scientists point to the Mayans, a culture that used a symbol for zero in the 6th century—a figure that resembled a shell, which is close to our zero. What is the problem with the invention of a zero symbol by the Mayans? Unlike more mobile cultures, they were not able to spread the word around the world; although others say that certain Mayan calendar dates—and thus, the symbol—were noted outside the Mayan region, especially by the Olmec, a pre-Columbian civilization living in south-central Mexico around 1500 to 400 B.C.E.

As you can see, there is no true agreement about who was the first to invent a symbol for zero. In fact, many scientists believe there may have been many symbols that represented zero invented by many ancient cultures—including some crude “goose eggs”—but the evidence has been either lost or destroyed over time. (For more information about the Mayans, see elsewhere in this chapter; for more about the history of zero, see “Mathematics throughout History.”)

What do we know about Babylonian mathematical tables?

Archeologists know that the Babylonians invented tables to represent various mathematical calculations. Evidence comes from two tablets found in 1854 at Senkerah on the Euphrates River (dating from 2000 B.C.E.; some researchers say 1800 to 1600 B.C.E.). One listed the squares of numbers up to 59, and the other the cubes of numbers up to 32 (for more about the second tablet, see above).

What was one of the earliest mathematical writings yet discovered?

To date, historians believe that one of the earliest mathematical writings came from the Babylonians—a clay tablet “written” around 2000 B.C.E. (although some researchers approximate the date at 1800 to 1600 B.C.E.). This clay chunk showed an image that looks like a square with two diagonal lines slicing the square equally—like an X in a square. In reality, it represents a sexagesimal numerical approximation of the square root of two—the length of the diagonal in a unit square. This was no doubt needed in the construction of ancient buildings and monuments, as being able to compute the sides of a triangle—not to mention square roots—was very necessary.

The Babylonians also used a method of division based on tables and the equation a/b = a × (1/b). With this equation, all that was necessary was a table of reciprocals; thus, the discovery of tables with reciprocals of numbers up to several billion.

They also constructed tables for the equation n³ + n², in order to solve certain cubic equations. For example, in the equation ax³ + bx² = c (note: this is in our modern algebraic notation; the Babylonians had their own symbols for such an equation), they would multiply the equation by a², then divide it by b³ to get (ax/b)³ + (ax/b)² = ca²/b³. If y = ax/b, then y³ + y² = ca²/b³—and could now be solved by looking up the n³ + n² table for the value of n that satisfies n³ + n² = ca²/b³. When a solution was found for y, then x was found by x = by/a. And the Babylonians did all this without the knowledge of algebra or the notation we are familiar with today.

What happened to the Mayans?

The Mayans were one of the most advanced civilizations of prehistory—one that excelled at many mathematically-related subjects as architecture, astronomy, and an elaborate hieroglyphic language. This culture, located in what is today’s southern Mexico, Guatemala, Belize, El Salvador, and some of Honduras, rose around 250 C.E. and collapsed around 900 C.E. Not everyone agrees on the reason for the Mayan demise, but there are many guesses, most of them a combination of events. Over the years, theories have ranged from a disastrous disease that killed off the civilization, to a natural disaster (such as an earthquake or small asteroid strike). Such a disaster would have killed off enough of the population and caused starvation—mainly because the land would be unusable after the event(s).

Does the Mayan calendar predict the end of the Earth?

Everyone likes a good mystery, and there seems to be one associated with the Mayan calendar. According to some interpretations, on December 21, 2012, the Mayan calendar “ends,” thus predicting a catastrophic end of the earth, mainly through a series of astronomical events—anything from destructive solar flares to asteroid strikes. This theory is based on what is called the Mayan “Long Count Calendar,” the longest period calendar so far found in the many calendars the culture developed.

The Long Count Calendar was used to document past and future Mayan events. Some of their shorter calendars were based on 52 years, or what would be thought of as a generation. Mathematically speaking, the Mayans determined that the Long Count Calendar would be “finished” after 5,126 years, but that is only its first cycle. Some modern interpretations predict that if, according to our current calendar, the Mayans began the calendar at 3114 B.C.E., then 5126 - 3114 is the year 2012—thus, the warnings, articles, books, and movies predicting the end of the world by that date. The actual day, December 21, was chosen because, everyone assumes, it’s the Northern Hemisphere’s Winter Solstice. But the actual date seems to be a moving target—in other words, it also could be December 23, based on the interpretation of 13 buctuns (a Mayan division of time), or close to 5,125.26 years.

But it doesn’t take a mathematician (or a rocket scientist) to realize the immediate flaws. First, such catastrophes don’t usually fall so neatly into a human interpretation of time—Mayans or not. Second, our present calendar has had so many changes and iterations, how can anyone truly “coordinate” the correct date for the catastrophe-filled day? (For more information about the many calendars over time, see elsewhere in this chapter.) And even then, not every translation of the Mayan calendar has been verified. In fact, interpreting the events during Mayan civilization based on their calendar(s) has been questioned by many researchers. The Mayans may have been excellent astronomers, but some of their mathematical skills and translations still remain a mystery to modern scientists.

Another theory proposes that the Mayan people may have overused the resources of their region, which had a direct (and irreparable) affect on the surrounding ecology. The best evidence for this has only recently been found. Scientists examining the many Mayan ruins believe that by 800 C.E., the people had cut down most of the surrounding trees to build large cities and monuments—after all, the Mayans had one of the densest populations in prehistory. Similar to today’s Amazon rainforest—and even modern day Guatemala—cutting down trees most likely (and dramatically) changed the local climate, causing not only extensive erosion of the soils, but also droughts. The results were a massive migration of people away from the Mayan cities and the eventual collapse of the civilization.

EGYPTIAN NUMBERS AND MATHEMATICS

Alexander the Great, depicted here in an 1899 painting of the Battle of Gaugamela, Iraq (331 B.C.E.), by artist Benjamin Ide Wheeler, conquered much of the known world and brought an end to the Babylonian civilization. The rise and fall of civilizations throughout history did much to influence the development of mathematics over the centuries.

Who were the Egyptians?

The Egyptians rose in prominence around 3000 B.C.E. in the area we now call Egypt, but their society was already advanced, urbanized, and expanding rapidly long before that time. Although their civilization arose about the same time that words and numbers were first written down in Mesopotamia, archeologists do not believe there was any sharing between the two cultures. The Egyptians already had writing and written numerals; plus, the Egyptian signs and symbols were taken exclusively from the flora and fauna of the Nile River basin. In addition, the Egyptians developed the utensils for writing signs about a thousand years earlier.

What type of numerals did the Egyptians use?

By about 3000 B.C.E., the Egyptians had a writing system based on hieroglyphs, or pictures that represented words. Their numerals were also based on hieroglyphs. They used a base 10 system of numerals: One unit, one ten, one hundred, and so on to one million. The main drawback to this system was the number of symbols needed to define the numbers.

Did the Egyptians eventually develop different numerals?

Yes, the Egyptians used another number system called hieratic numerals after the invention of writing on papyrus. This allowed larger numbers to be written in a more compact form. For example, there were separate symbols for 1 through 9; 10, 20, 30, and so on; 100, 200, 300, and so on; and 1,000, 2000, 3,000, and so on.

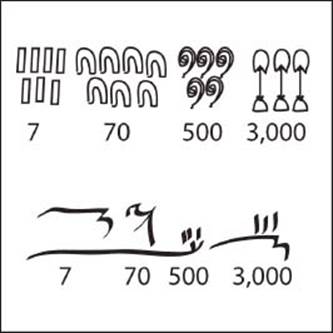
The number 3,577 is represented above using hieroglyphs (top) and hieratic symbols (bottom). Notice these numbers are read from right to left.

The symbols for 1/5, 1/10, and ½ are represented above using hieroglyphs.

The only drawback was that the system required memorization of more symbols—many more than for hieroglyphic notation. It took four distinct hieratic symbols to represent the number 3,577; it took no less than 22 symbols to represent the same number in hieroglyphs, but most of those symbols were redundant.

Both hieroglyphic and hieratic numerals existed together for close to 2,000 years—from the third to the first millennium B.C.E. In general, hieroglyph numerals were used when carved on such objects as stone obelisks, palace and temple walls, and tombs. The hieratic symbols were much faster and easier to scribe, and were written on papyrus for records, inventories, wills, or for mathematical, astronomical, economic, legal—or even magical—works.

Even though it is thought that the hieratic symbols were developed from the corresponding hieroglyphs, the shapes of the signs changed considerably. One reason in particular were the reed brushes used to write hieratic symbols; writing on papyrus differed greatly from writing using stone carvings, thus the need to change the symbols to fit the writing devices. And as kingdoms and dynasties changed, the hieratic numerals changed, too, with users having to memorize the many distinct signs.

What are some examples of Egyptian multiplication?

Egyptian multiplication methods did not require a great deal of memorization, just a knowledge of the two times tables. For a simple example, to multiply 12 times 16, they would start with 1 and 12. Then they would double each number in each row (1 × 2 and 12 × 2; 2 × 2 and 24 × 2; and so on) until the number 16, resulting in the answer 192:

Another example computes a number that is not a multiple in the row, such as 37 times 19:

First, do the usual procedure by starting with 1 and 19, then doubling the numbers until you get to 32 (if you double 32 [_ 64], you’ve overshot the number 37). Because 37 is higher than 32, go back over the list on the left hand side, figure out which numbers, with 32, add up to 37 (1, 4, and 32); then add the numbers that correspond to those numbers, to the right (19, 76, and 608), which equals the answer: 703. And you didn’t even need a calculator!

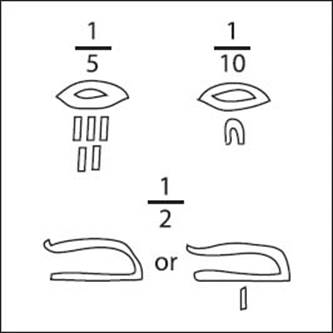
Did the Egyptians use fractions?

Yes, the Egyptian numbering system dealt with fractions, albeit with symbols that do not resemble modern notation. Fractions were written by placing the hieroglyph for “mouth” over the hieroglyph for the numerical expression. For example, 1/5 and 1/10 would be seen as the first two illustrations represented in the box on page 12. Other fractions, such as the two symbols for ½ (see illustration on page 12), also have special signs.

What were the problems with the Egyptian number system?

The Egyptian number system had several problems, the most obvious that it was not written with certain arithmetic calculations in mind. Similar to Roman numerals, Egyptian numbers could be used for addition and subtraction, but not for simple multiplication and division.

All was not lost, however, as the Egyptians devised a way to do multiplication and division that involved addition. Multiplying and dividing by 10 was easy with hieroglyphics— just replace each symbol in the given number by the sign for the next higher order. To multiply and divide by any other factor, Egyptians devised the tabulations based on the two times tables, or a sequence of duplications.

Where does most of our knowledge of Egyptian mathematics originate?

Most of our knowledge of Egyptian mathematics comes from writings on papyrus, a type of writing paper made in ancient Egypt from the pith and long stems of the papyrus plant. Most papyri no longer exist, as the material is fragile and disintegrates over time. But two major papyri associated with Egyptian mathematics have survived.

Named after Scottish Egyptologist A. Henry Rhind, the Rhind papyrus is about 19 feet (6 meters) long and 1 foot (1/3 meter) wide. It was written around 1650 B.C.E.by Ahmes, an Egyptian scribe who claimed he was copying a 200-year-old document (thus the original information is from about 1850 B.C.E.). This papyrus contains 87 mathematical problems; most of these are practical, but some teach manipulation of the number system (though with no application in mind). For example the first six problems of the Rhind papyrus ask the following: in problem 1, how to divide n loaves between 10 men, in which n = 1; in problem 2, n = 2 ; in problem 3, n = 6; in problem 4, n = 7; in problem 5, n = 8; and in problem 6, n = 9. In addition, 81 out of the 87 problems involve operating with fractions, while other problems involve quantities and even geometry. Rhind purchased the papyrus in 1858 in Luxor; today it resides in the British Museum in London.

Written around the twelfth Egyptian dynasty, and named after the Russian city, the mathematical information on the Moscow papyrus is not ascribed to any one Egyptian, as no name is recorded on the document. The papyrus contains 25 problems similar to those in the Rhind papyrus, and many that show the Egyptians had a good grasp of geometry, including a formula for a truncated pyramid. It now resides in the Museum of Fine Arts in Moscow.

GREEK AND ROMAN MATHEMATICS

Why was mathematics so important to the Greeks?

With a numbering system in place and knowledge from the Babylonians, the Greeks became masters of mathematics, with the most progress made from 300 B.C.E. to 200 C.E., although the Greek culture had been in existence long before that time. The Greeks changed the nature and approach to math, and they considered it one of the most—if not the most—important subjects in science. The main reason for their proclivity towards mathematics is easy to understand: The Greeks preferred reasoning over any other activity. Mathematics is based on reasoning, unlike many scientific endeavors that require experimentation and observation.

Who were some of the most influential Ionian, Greek, and Hellenic mathematicians?

The Ionians, Greeks, and Hellenics had some of the most progressive mathematicians of their time—a list that includes such mathematicians as Heron of Alexandria, Zeno of Elea, Eudoxus of Cnidus, Hippocrates of Chios, and Pappus. The following are only a few of the more influential mathematicians.

Ptolemy (center), depicted in this 1632 engraving discussing ideas with Aristotle (left) and Copernicus (right), discovered valuable concepts concerning cartography, geometry, and astronomy.

· Thales of Miletus (c. 625-c. 550 B.C.E., Ionian), besides being purportedly the founder of a philosophy school and the first recorded Western philosopher known, Thales made great contributions to Greek mathematics, especially by presenting Babylonian mathematics to the Greek culture. His travels as a merchant undoubtedly exposed him to the geometry involved in measurement. Such concepts eventually helped him to introduce geometry to Greece, solving such problems as the height of the pyramids (using shadows), the distance of ships from a shoreline, and reportedly predicting a solar eclipse.

· Hipparchus of Rhodes (c. 170-c. 125 B.C.E., Greek; also seen as Hipparchus of Nicaea) was an astronomer and mathematician who is credited with creating some of the basics of trigonometry. This helped immensely in his astronomical studies, including the determination of the Moon’s distance from Earth.

· Geminus (c. 1st century B.C.E., Greek) was an astronomer and mathematician; his astronomy text, the Introduction to the Phenomena, still survives today, and was an introductory astronomy book for students. His mathematical texts did not survive as well, and most of his extensive mathematical writings survive in the writings of his contemporaries and beyond.

· Claudius Ptolemaeus (or Ptolemy; c. 100-c. 170 C.E., Hellenic) was one of the most influential Greeks, not only in the field of astronomy, but also in geometry and cartography. Basing his works on Hipparchus, Ptolemy developed the idea of epicycles, in which each planet revolves in circular orbits, and each around an Earth-centered universe. The Ptolomaic way of explaining the solar system—which we now know is incorrect—dominated astronomy for more than a thousand years.

· Diophantus (c. 210-c. 290 C.E.) was considered by some scholars to be the “father of algebra.” In his treatise Arithmetica, he solved equations in several variables for integral solutions, or what we called diophantine equations today. (For more about these equations, see “Algebra.”) He also calculated negative numbers as solutions to some equations, but he considered such answers absurd.

What were Archimedes’s greatest contributions to mathematics?

Historians consider Archimedes (c. 287-212 B.C.E., Hellenic) to be one of the greatest Greek mathematicians of the classic era. Known for his discovery of the hydrostatic principle, he also excelled in the mechanics of simple machines; computed close limits on the value of “pi” by comparing polygons inscribed in and circumscribed about a circle; worked out the formula to calculate the volume of a sphere and cylinder; and expanded on Eudoxus’ method of exhaustion that would eventually lead to integral calculus. He also created a way of expressing any natural number, no matter how large; this was something that was not possible with Greek numerals. (For more information about Archimedes, see “Mathematical Analysis” and “Geometry and Trigonometry.”)

The Greek mathematician Euclid contributed to the development of arithmetic and the geometric theory of quadratic equations.

What Greek mathematician made major contributions to geometry?

The Greek mathematician Euclid (c. 325-c. 270 B.C.E.), contributed to the development of arithmetic and the geometric theory of quadratic equations. Although little is known about his life— except that he taught in Alexandria, Egypt—his greatest contributions to geometry are well understood. The elementary geometry many of us learn in high school is still largely based on Euclid. His thirteen books of geometry and other mathematics, titled Elements (or Stoicheion in Greek), were classics of his day. The first six volumes offer elementary plane geometry; the other books present the theory of numbers, certain problems in arithmetic (on a geometric basis), and solid geometry. He also defines basic terms such as point and line, certain related axioms and postulates, and then a number of statements logically deduced from the definitions, axioms, and postulates. (For more information on axiom and postulates, see “Foundations of Mathematics”; for more information about Euclid, see “Geometry and Trigonometry.”)

What was Pythagoras’s importance to mathematics?

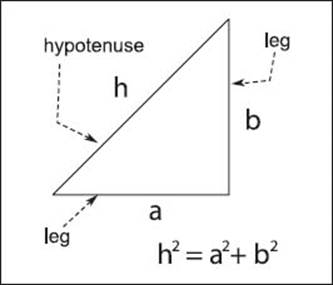
The Pythagorean theorem is an easy way to determine the length of one side of a right triangle, given one knows the length of the other two sides.

Although the Chinese and Mesopotamians had discovered it over a thousand years before, most people credit the Greek mathematician and philosopher Pythagoras of Samos (c. 582-c. 507 B.C.E.) with being the first to prove the Pythagorean theorem. This is a famous geometry theorem relating the length of a right-angled triangle’s hypotenuse (h) to the lengths of the other two sides (a and b).

In other words, for any right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides.

What were Pythagoras’s other contributions?

It is interesting that the Pythagorean theorem was not Pythagoras’s only contribution. He is considered the first pure mathematician. He also founded a school that stressed a fourfold division of knowledge, including number theory (deemed the most important of the pursuits at the school and using only the natural numbers), music, geometry, and astronomy (these subjects were called the quadrivium in the Middle Ages). Along with logic, grammar, and rhetoric, these studies collectively formed what was deemed the essential areas of knowledge for any well-rounded person.

Pythagoras not only taught these subjects, but also reincarnation and mysticism, establishing an order similar to, or perhaps influenced by, the earlier Orphic cult. The true lives of Pythagoras and his followers (who worshipped Pythagoras as a demigod) are a bit of a mystery, as they followed a strict code of secrecy and regarded their mathematical studies as something of a black art. The fundamental belief of the Pythagoreans was that “all is number,” or that the entire universe—even abstract ethical concepts like justice—could be explained in terms of numbers. But they also had some interesting non-mathematical beliefs, too, including an aversion to beans.

Although the Pythagoreans were influential in the fields of mathematics and geometry, they also made important contributions in astronomy and medicine, and were the first to teach that the Earth revolved around a fixed point (the Sun). This idea would be popularized centuries later by Polish astronomer Nicolaus Copernicus (1473–1543). By the end of the 5th century B.C.E., the Pythagoreans would become social outcasts; many of them were killed as people grew angry at the group’s interference with traditional religious customs.

Who was the first recorded female mathematician?

The first known female mathematician was Hypatia of Alexandria (370–415), who was probably tutored by her mathematician and philosopher father, Theon of Alexandria, who taught at the Museum of Alexandria in Egypt. Around 400, she became the head of the Platonist school at Alexandria, lecturing on mathematics and philosophy. It is thought that she also invented the plane astrolabe, the graduated brass hydrometer, and the hydroscope (possibly with Synesius of Greece, once her student and later her colleague at the school). Little is known of her writings—thought to be works on mathematics, astronomy, and philosophy—and more legend is known of her than any true facts. It is thought that she was eventually killed by a mob egged on by a Christian bishop, Cyril, who felt the contrary-to-the-norm (and pagan) Hypatia did not know her place.

What is the origin of Roman numerals?

Because the history of Roman numerals is not well documented, their origin is highly debated. It is thought that the numerals were developed around 500 B.C.E., partially from primitive Greek alphabet symbols that were not incorporated into Latin. The actual reasons for the seven standard symbols are also argued. Some researchers believe the symbol for 1 (I) was derived from one digit on the hand; the symbol for 5 (V) may have developed because the outstretched hand held vertically forms a “V” from the space between the thumb and first finger; the symbol for 10 (X) may have been two Vs joined at the points, or it may have had to do with the way people or merchants used their hands to count resembled an “X.” All the reasons so far have merely been educated guesses.

Archimedes discovered a clever way to measure the volume of an irregularly shaped object using water displacement.

How ever the symbols were developed, they were used with efficiency and with remarkable aptitude by the Romans. Unlike the ancient Greeks, the Romans weren’t truly interested in “pure” math, such as abstract geometry. Instead, they concentrated on “applied math,” using mathematics and their Roman numerals for more practical purposes, such as building roads, temples, bridges, and aqueducts; for keeping merchant accounts; and for managing supplies for their armies.

What is the story behind “Archimedes in the bathtub”?

One of the most famous stories of Archimedes involves royalty: When Hiero II of Syracuse, King of Sicily, wanted to determine if a crown (actually, a wreath) he had ordered was truly pure gold or alloyed with silver—in other words, whether or not the Royal Goldsmith had substituted some of the gold with silver. The king called Archimedes to solve the problem. The Greek mathematician knew that silver was less dense than gold (or silver was not as heavy as gold), but without pounding the crown into an easily weighed cubic shape, he didn’t know how to determine the relative density of the irregularly-shaped crown.

Perplexed, the mathematician did what we all do to get good ideas: he took a bath. As he entered the tub, he noticed how the water rose, which made him realize that the volume of water that fell out of the tub was equal to that of the volume in his body. Legend has it Archimedes ran naked through the streets shouting “Eureka!” (“I have found it!”). He knew that a given weight of gold represented a smaller volume than an equal weight of silver because gold is much denser than silver, so not as much is needed to displace the water. Therefore, a specific amount of gold would displace less water than an equal weight of silver.

The next day, Archimedes submerged the crown and an amount of gold equal to what was supposed to be in the crown. He found that Hiero’s crown displaced more water than an equal weight of gold, thus proving the crown was alloyed with a less dense material (the silver) and not pure gold. This eventually led to the hydrostatic principle, as it is now called, presented in Archimedes’s appropriately-named treatise, On Floating Bodies. As for the goldsmith, he was beheaded for stealing the king’s gold.

Centuries after the Roman Empire fell, various cultures still used Roman numerals. Even today, the symbols are still in existence; they are used on certain timepieces, in formal documents, and for listing dates in the form of years. For example, just watch the end credits of your favorite movie or television program and you will often see the movie’s copyright date in Roman numerals.

What are the basic Roman numerals and how are they used?

There are only seven basic Roman numerals, as seen in the following chart:

Why were early Greek calendars such a mess?

Unlike the Mesopotamian cultures, the early Greeks paid less attention to astronomy and more to cosmology (they were interested in studying where the Earth and other cosmic bodies stand in relation to the universe). Because of this, their astronomical observations were not accurate, creating confusing calendars. This also led to a major conundrum: Almost every Greek city kept time differently. In fact, during the Greek and Hellenistic times, most dates were given in terms of the Olympiads. This only created another time-keeping problem: If something happened during the 10th Olympiad, it meant the event occurred within a four year span. Such notation creates headaches for historians, who end up making educated guesses as to the actual dates of Greek events, important people’s deaths and births, and sundry other historical occurrences.

There are many rules, of course, to this method of writing numerals. For example, although the way to write large numbers like 8,000 would be “MMMMMMMM,” it is very cumbersome. In order to work with such large numbers, one rule was to write a bar over a numeral, meaning to multiply by 1,000. Thus, 8,000 would be VIII—equal to our Hindu-Arabic number 8—with a bar over the entire Roman numeral.

OTHER CULTURES AND EARLY MATHEMATICS

What did the Chinese add to the study of mathematics?

Despite the attention the Greeks have received concerning the development of mathematics, the Chinese were by no means uninterested in it. About the year 200 B.C.E., the Chinese developed place value notation, and 100 years later, they began to use negative numbers. By the turn of the millennium and a few centuries beyond, they were using decimal fractions (even for the value of “pi” [π]) and the first magic squares (for more information about math puzzles, see “Recreational Math”). By the time European cultures began to decline—from about 530 to 1000 C.E.—the Chinese were contributing not only to the field of mathematics, but also to the study of magnetism, mechanical clocks, physical laws, and astronomy.

What was the House of Wisdom?

Around 786, the fifth Caliph of the Abbasid dynasty began with Caliph Harun al-Rashid, a leader who encouraged learning, including the translation of many major Greek treatises into Arabic, such as Euclid’s Elements. Al-Ma’mun (786–833), the next Caliph, was even more interested in scholarship, creating the House of Wisdom in Baghdad, one of several scientific centers in the Islamic Empire. Here, too, Greek works such as Galen’s medical writings and Ptolemy’s astronomical treatises were translated, not by language experts ignorant of mathematics, but by scientists and mathematicians such as Al-Kindi (801–873), Muhammad ibn Musa al-Khuwarizmi (see below), and the famous translator Hunayn ibn Ishaq (809–873).

A famous Caliph whose reign was immortalized in the book One Thousand and One Arabian Knights, Harun al-Rashid promoted education among his subjects, including the mathematical writings of the Greeks.

What is the most famous Chinese mathematics book?

The Jiuzhang suanshu, or Nine Chapters on the Mathematical Art, is the most famous mathematical book to come out of ancient China. This book dominated mathematical development for more than 1,500 years, with contributions by numerous Chinese such as Xu Yue (c. 160-c. 227), though his contributions were lost. It contains 246 problems meant to provide methods to solve everyday questions concerning engineering, trade, taxation, and surveying.

What are some familiar Arabic terms used in mathematics?

There are numerous Arabic terms we use today in our studies of mathematics. One of the most familiar is the term “algebra,” which came from the title of the book Al jabr w’al muqabalah by Persian mathematician Muhammad ibn Musa al-Khuwarizmi (783-c. 850; also seen as al-Khowarizmi and al-Khwarizmi); he was a scholar who described the rules needed to do mathematical calculations in the Hindu-Arabic numeration system. The book, whose title is roughly translated as Transposition and Reduction, explains all about the basics of algebra, including methods for solving all equations of the first and second degree with positive roots. (For more information, see the chapter on “Algebra.”)

Who was al-Karaji, also called al-Karkhi?

One of the most well-known mathematicians from what is now called Iraq was al-Karaji (c. 953-c. 1029 C.E.). The biggest confusion seems to be his name: al-Karaji may be from a city in Iran called Karaj, which may mean his family was from the area. The name al-Karkhi may be from Karkh, or a suburb of Baghdad outside the southern gate of the original city, not the city itself. Historians don’t agree—and they also don’t agree with the mathematical contributions of this man. Some say he developed many mathematical contributions, such as multiplication of polynomials, and changed algebra from being collected to geometric operations, and made them more user-friendly with arithmetical operations. Still others say that he only copied other mathematicians’ works. Either way, he’s also credited with making rules for measuring plane and solid figures, and describing how to weigh different substances.

Another Arabic derivation is “algorithm” from the Latinized version of Muhammad ibn Musa al-Khuwarizmi’s own name. Over time, his named evolved from al-Khuwarizmi to Alchoarismi, then Algorismi, Algorismus, Algorisme, and finally Algorithm.

Who was Omar Khayyám?

Omar Khayyám (1048–1131) is not well-known for math, but for being immortalized by Edward FitzGerald, the nineteenth century English poet who translated Khayyám’s own 600 short four line poems, the Rubaiyat. (However, FitzGerald’s translations were not exact—and most scholars agree that Khayyám did not state, “a jug of wine, a loaf of bread, and Thou.” Those words were actually conceived by FitzGerald.)

In reality, Khayyám was actually known as al-Khayyámi, the Persian mathematician, poet, and astronomer whose contributions were many. He wrote the Treatise on Demonstration of Problems of Algebra, a book that contains a complete classification of cubic equations with geometric solutions—all found by means of intersecting conic sections. He solved the general cubic equation hundreds of years before Niccoló Tartaglia in the 16th century, but his work only had positive roots, since it was completely geometrical (see this chapter for more about Tartaglia). He also calculated the length of the year to be 365.24219858156 days—a remarkably accurate result for his time—and proved that algebra was definitely related to geometry.

MATHEMATICS AFTER THE MIDDLE AGES

Who first introduced Arabic notation and the concept of zero to Europe?

Italian mathematician Leonardo of Pisa (c. 1170-c. 1250, who was also known as Fibonacci, or “son of Bonacci,” although some historians say there is no evidence that he or his contemporaries ever used the name) brought the idea of Arabic notation and the concept of zero to Europe. His book Liber abaci (The Book of the Abacus) not only introduced zero, but the arithmetic and algebra he learned in Arab countries. Another book, Liber quadratorum (or The Book of the Square) was the first major European advance in number theory in a thousand years. He is also responsible for presenting the Fibonacci sequence. (For more information about Fibonacci and the Fibonacci sequence, see “Math Basics.”)

What were the major reasons for advances in 16th-century European mathematics?

There are several reasons for advances in mathematics at the end of the Middle Ages. The major reason, of course, was the beginning of the Renaissance, a time when there was a renewed interest in learning. Another important event that pushed mathematics was the invention of printing, which made many mathematics books, along with useful mathematical tables, available to a wide audience. Still another advancement was the replacement of the clumsy Roman numeral system by Hindu-Arabic numerals. (For more information about the Hindu-Arabic numerals, see “Math Basics.”)

Who was Adam Ries?

Adam Ries (1492–1559) was the first to write several books teaching the arithmetic method by the old abacus and new Indian methods; his books also presented the basics of addition, subtraction, multiplication, and division. Unlike most books of his time that were written in Latin and only understood by mathematicians, scientists, and engineers, Ries’s books were written in his native German and were therefore understood by the general public. The books were also printed, making them more readily available to a wider audience.

Who was François Viète?

French mathematician François Viète (or Franciscus Vieta, 1540-1603) is often called the “founder of modern algebra.” He introduced the use of letters as algebraic symbols (although Descartes [see ahead] introduced the convention of letters at the end of the alphabet [x, y, …] for unknowns and beginning of the alphabet [a, b, …] for knowns), and connected algebra with geometry and trigonometry. He also included trigonometric tables in his Canon Mathematicus (1571)—along with the theory behind their construction. This book was originally meant to be a mathematical introduction to his unpublished astronomical treatise, Ad harmonicon coeleste. (For more about Viète, see “Algebra” and “Geometry and Trigonometry.”)

Scottish mathematician John Napier first conceived the idea of logarithms.

What century produced the greatest revolution in mathematics?

Many mathematicians and historians believe that the 17th century saw not only the unprecedented growth of science, but the greatest revolution in mathematics. This century included the discovery of logarithms, the study of probability, the interactions between mathematics, physics, and astronomy, and the development of one of the most profound mathematical studies of all: calculus.

Who explained the nature of logarithms?

Scottish mathematician John Napier (1550–1617) first had the idea about logarithms in 1594. It took him twenty years, until 1614, to publish a canon of logarithms called Mirifici logarithmorum canonis descripto (Description of the wonderful canon of logarithms). The canon explains the nature of logarithms, gives their rules of use, and offers logarithmic tables. (For more about logarithms, see “Algebra.”)

What was the scandal between mathematicians working on cubic and quartic equations?

The early work on cubic equations was a tale of telling secrets—all taking place in Italy. Antonio Maria Fiore (c. 1526-?)—considered a mediocre mathematician by scholars—received the secret of solving the cubic equation from his teacher Scipione del Ferro (1465–1526), who was the one who actually discovered the formula and told Fiore just before his death. It didn’t take long for Fiore to spread the rumor of its solution. A self-taught Italian mathematical genius known as Niccoló Tartaglia (1500-c. 1557; nicknamed “the stutterer”) was already discovering how to solve many kinds of cubic equations. Not to be outdone, Tartaglia pushed himself to solve the equation x³+ mx² = n—bragging about it when he had accomplished the task.

Fiore was outraged—a fortuitous event for the study of cubic (and eventually quartic) equations. Demanding a public contest between himself and Tartaglia, the mathematicians were to give each other 30 problems with 40 to 50 days in which to solve them. Each problem solved earned a small prize, but the winner would be the one to solve the most problems. In the space of 2 hours, Tartaglia solved all Fiore’s problems—all of which were based on x³ + mx² = n. Eight days before the end of the contest, Tartaglia had found the general method for solving all types of cubic equations—while Fiore had solved none of Tartaglia’s problems.

The story did not end there: Around 1539, Italian physician and mathematician Girolamo Cardano (1501-1576; in English, known as Jerome Cardan) stepped into the picture. Impressed with Tartaglia’s abilities, Cardano asked him to visit. He also convinced Tartaglia to divulge his secret solution of the cubic equation, with Cardano promising not to tell until Tartaglia published his results.

Apparently, keeping secrets was not practiced in Italy at this time, and Cardano eventually beat Tartaglia to publication. Cardano eventually encouraged his student Luigi (Ludovico) Ferrari (1522-?) to work on solving the quartic equation (or the general polynomial equation of the fourth degree). Ferrari did just that, and in 1545, Cardano published his Latin treatise on algebra, Ars Magna (The Great Art)—which included a combination of Tartaglia’s and Ferrari’s works in cubic and quartic equations.

Who originated Cartesian coordinates?

Cartesian coordinates are a way to find the location of a point using distances from perpendicular axes. (For more information about coordinates, see “Geometry and Trigonometry.”) The first steps toward such a coordinate system was suggested by French philosopher, mathematician, and scientist René Descartes (1596-1650; in Latin, Renatus Cartesius); he was the first to publish a work explaining how to use coordinates for finding points in space. Around the same time, Pierre de Fermat developed the same idea independently (see below). Both Descartes’s and Fermat’s ideas would lead to what is now known as Cartesian coordinates.

Descartes is also considered by some to be the founder of analytical geometry. He contributed to the ideas involved in negative roots and exponent notation, explained the phenomenon of rainbows and the formation of clouds, and even dabbled in psychology.

Who was Pierre de Fermat?

French mathematician Pierre de Fermat (1601–1665) made many contributions to early methods leading to differential calculus; he was also considered by some to be the founder of modern number theory (see “Math Basics”) and did much to establish coordinate geometry, eventually leading to Cartesian coordinates. He supposedly proved a theorem eventually called “Fermat’s last theorem.” It states that the equation xⁿ + yⁿ = zⁿ has no non-zero integer solutions for x, y, and z when n is greater than 2. But there is no proof of Fermat’s “proof,” making most mathematicians skeptical about his supposed discovery.

Was Fermat’s last theorem finally solved?

Just before the end of the 19th century, German industrialist and amateur mathematician Paul Wolfskehl, on the brink of suicide, began to explore a book on Fermat’s last theorem. Enchanted with the numbers, he forgot about dying and instead believed that mathematics had saved him. To repay such a debt, he left 100,000 marks to the Göttingen Academy of Science as a prize to anyone who could publish the complete proof of Fermat’s last theorem. Announced in 1906 after Wolfskehl’s death, thousands of incorrect proofs were turned in, but no true proof was offered.

Pierre de Fermat made significant contributions to geometry, number theory, and calculus.

But people kept trying—and failing. Fermat’s last theorem was finally solved in 1994 by English mathematician Andrew John Wiles (1953-). Wiles was offered the Wolfskehl prize in 1997. By that time, the original $2 million had been affected by not only hyperinflation but also the devaluation of the mark, reducing its value to $50,000 (in 1997 dollars). But for Wiles, it didn’t matter; his proving the last theorem had been a childhood dream.

Although it has so far stood up to mathematical scrutiny, it is interesting to note that some mathematicians do not believe Wiles uncovered the true proof of Fermat’s last theorem. Instead, because many of the mathematical techniques used by Wiles were developed within the last decades (some even by Wiles himself), Wiles’s proof— although a masterpiece of mathematics—could not possibly be the same as Fermat’s. Still other mathematicians wonder about Fermat’s words, too, in claiming that he had found a proof. Was it really a proven or flawed proof he was talking about? Or was he such a genius that he took the proof he was able to see, in his time, to his grave? Like so many historical mathematical mysteries, we may never know.

Who began the mathematical study of probability?

French scientist and religious philosopher Blaise Pascal (1623–1662) is known not only for the study of probability, but many other mathematical-oriented advances, such as a calculation machine (invented at age 19 to help his father with tax calculations, but it performed only additions), hydrostatics, and conic sections. He is also credited (along with Fermat) as the founder of modern theory of probability. (For more information about probability, see “Applied Mathematics.”)

Seventeenth-century scientist Blaise Pascal was the founder of mathematical probability, as well as other achievements, such as devising one of the first calculating machines.

Most people know about Sir Isaac Newton’s famous laws of motion. He also invented differential and integral calculus.

Who was Sir Isaac Newton?

Sir Isaac Newton (1642–1727) was an English mathematician and physicist considered by some to be one of the greatest scientists who ever lived. He was credited with inventing differential calculus in 1665 and integral calculus the following year. (For more information about calculus, see “Mathematical Analysis.”) The list of his achievements—mathematical and scientific—does not end there: He is also credited as the discoverer of the general binomial theorem, worked on infinite series, and even made advancements in optics and chemistry.

Some of Newton’s greatest contributions include the development of the law of universal gravitation, rules of planetary orbits, and sundry other astronomical concepts. By 1687, Newton had written one of his most famous books The Principia or Philosophiae naturalis principia mathematica (The Mathematical Principles of Natural Philosophy), which is often called the greatest scientific book ever written. In it Newton presents his theories of motion, gravity, and mechanics. Although he had developed calculus earlier, he still used the customary classical geometry to work out physical problems within the book.

Who was Baron Gottfried Wilhelm Leibniz?

A contemporary of Isaac Newton, German philosopher and mathematician Baron Gottfried Wilhelm Leibniz (1646–1716) is considered by some to be a largely forgotten mathematician, although his contributions to the field were just as important as Newton’s. He is often called the founder of symbolic logic; he introduced the terms coordinate, abscissas, and ordinate for the field of coordinate geometry; he invented a machine that could do multiplication and division; he discovered the well-known series for pi (π) divided by 4 (π/4) that bears his name; and he independently developed infinitesimal calculus and was the first to describe it in print. Because his work on calculus was published three years before Isaac Newton’s, Leibniz’s system of notation was universally adopted.

Who was considered the first statistician?

English statistician and tradesman John Graunt (1620–1674) was the first true statistician, writing the first book on statistics, although statistics in a simpler form was known long before. Graunt, a draper by profession, was the first to use a compilation of data—in this case the records of bills of mortality, or the records of how and when people died in London from 1604 to 1661. In his Natural and Political Observations Made Upon the Bills of Mortality, he determined certain inclinations, such as more boys were born than girls, women live longer than men, etc. He also developed the first mortality table, which showed how long a person might expect to live after a certain age, something familiar to us all, especially in fields such as insurance and health.

Why was the Bernoulli family important to mathematics?

The Bernoulli (also seen as Bernouilli) family of the 17th and 18th centuries is synonymous with mathematics and science. One of the developers of ordinary calculus, calculus of variations, and the first to use the word integral was Jacob Bernoulli (1654-1705; also known as Jakob, Jacques, or James). He also wrote about the theory of probability, is often credited for developing the field of statistics, and discovered a series of numbers that bear his name: the coefficients of the exponential series expansion of x/(1 - e^-x).

Not to be outdone, his brother Johann (1667-1748; also known as Jean or John) contributed to the field of integral and exponential calculus, was the founder of calculus of variations, and worked on geodesics, complex numbers, and trigonometry. His son was not far behind: Daniel Bernoulli (1700–1782) was considered the first mathematical physicist, publishing Hydrodynamica in 1738, which included his now famous principle named in his honor (Bernoulli’s principle); and he brought out two ideas that were ahead of his time by many years: the law of conservation of energy and the kinetic-molecular theory of gases.

The Bernoulli legacy did not end there, with family members continuing to make great mathematical and scientific contributions. There were two Nicolaus Bernoullis; one, the brother of Jacob and Johann (1662–1716), was professor of mathematics at St. Petersburg, Russia’s Academy of Sciences; the other, the son of Johann and brother of Daniel (1695–1726), was also a mathematician. Another Johann Bernoulli (17101790) was another son of Johann (and brother of Daniel), who succeeded his father in the chair of mathematics at Basel, Switzerland, and also contributed to physics. The younger Johann also had a son named Johann (1746–1807), who was astronomer royal at Berlin and also studied mathematics and geography. Finally, Jacob Bernoulli (1759–1789), yet another son of the younger Johann, succeeded his uncle Daniel in teaching mathematics and physics at St. Petersburg, but met an untimely early death by drowning.

What was in Joseph-Louis Lagrange’s letter to Jean le Rond d’Alembert?

Italian-French astronomer and mathematician Comte Joseph-Louis Lagrange (1736–1813) was most known for his work in mathematical astronomy, including many functions, theories, etc. that bear his name (for example, Lagrange point, Lagrange’s equations, Lagrange’s theorem, Lagrangian function). His mentor was none other than French scientist Jean le Rond d’Alembert (1717–1783)—a physicist who expanded on Newton’s laws of motion, contributed to the field of fluid motion, described the regular changes in the Earth axis, and was the first to use partial differential equations in mathematical physics. He even had time to edit, along with French philosopher Denis Diderot (1713–1784), the Encyclopedié, a 17-volume encyclopedia of scientific knowledge published from 1751 to 1772.

But apparently living in the years of such mathematical enlightenment had its drawbacks. In 1781, Lagrange wrote a letter to d’Alembert about his greatest fear: that the field of mathematics had reached its limit. At that point in time, Lagrange believed everything mathematical had been discovered, uncovered, and calculated. Little did he realize that mathematics was only in its infancy.

Who was one of the most prolific mathematicians who ever lived?

Swiss mathematician Leonhard Euler (1707–1783) is considered to be one of the most prolific mathematicians who ever lived. In fact, his accomplishments are beyond the scope of this text. Suffice it to say that his collected works number more than seventy volumes, with contributions in pure and applied mathematics, including the calculus of variations, analysis, number theory, algebra, geometry, trigonometry, analytical mechanics, hydrodynamics, and the lunar theory (calculation of the motion of the moon). Euler was one of the first to develop the methods of the calculus on a wide scale. His most famous book, Elements, rapidly became a classic; and he wrote a geometry textbook (Yale University was the first American college to use the text).

Although half-blind for much of his life—and totally blind for his last seventeen years—he still had a near-legendary skill at calculation. Among his discoveries are the differential equation named for him (a formula relating the number of faces, edges, and vertices of a polyhedron, although Euler’s formula was discovered earlier by René Descartes); and a famous equation connecting five fundamental numbers in mathematics. Like many in the Bernoulli family, Euler eventually worked at the Academy of Sciences in St. Petersburg, Russia, a center of learning founded by Peter the Great.

Who was Karl Friedrich Gauss?

German mathematician, physicist, and astronomer Karl Friedrich Gauss (1777-1855; also seen as Johann Carl [or Karl] Friedrich Gauss) was considered one of the greatest mathematicians of his time—some have even compared him to Archimedes and Newton. His greatest mathematical contributions were in the fields of higher arithmetic and number theory. He discovered the law of quadratic reciprocity; determined the method of least squares (independently of French mathematician Adrien-Marie Legendre [1752-1833]); popularized the symbol “i” as the square root of negative 1 (although Euler first used the symbol); did extensive investigations in the theory of space curves and surfaces; made contributions to differential geometry; and the list goes on. In 1801, after the discovery (and subsequent loss) of the first asteroid, Ceres, by Giuseppe Piazzi, Gauss calculated the object’s orbit with little data; the asteroid was found again thanks to his calculations. He further calculated the orbits of asteroids found over the next few years.

English mathematician George Boole was the first to develop ideas on symbolic logic, that is, the use of symbols to represent logical principles.

Who developed the first ideas on symbolic logic?

English mathematician George Boole (1815–1864) was the first to develop ideas on symbolic logic, that is, the use of symbols to represent logical principles. He proposed this in his treatise, An Investigation of the Laws of Thought, on Which are Founded the Mathematical Theories of Logic and Probabilities, written in 1854. Today, this is called Boolean algebra. (For more information about Boole, see “Algebra”; for more information about symbolic logic, see “Foundations of Mathematics.”)

INTO MODERN MATHEMATICS

Who first developed set theory?

German mathematician George (Georg) Ferdinand Ludwig Philipp Cantor (1845–1918) was not only known for his work on transfinite numbers, but also for his development of the set theory, which is the basis of modern mathematical analysis (for more information on set theory, see “Foundations of Mathematics”). His Mathematische Annalen was a basic introduction to set theory. Unlike most long evolutionary histories of mathematical subjects, Cantor’s set theory was his creation alone. In the late 19th century, Cantor also developed the Continuum Hypothesis. He realized that there were many different sized infinities, further conjecturing that two particular infinities constructed by different processes were the same size.

What was the Principia Mathematical

In 1910, the first volume of the Principia Mathematica was published by Welsh mathematician and logician Bertrand Arthur William Russell (1872–1970) and English mathematician and philosopher Alfred North Whitehead (1861–1947). This book was an attempt to put mathematics on a logical foundation, developing logic theory as a basis for mathematics. It gave detailed derivations of many major theorems in set theory, examined finite and transfinite arithmetic, and presented elementary measure theory. The two mathematicians published three volumes, but the fourth, on geometry, was never completed.

On their own, both men did a great deal to advance mathematics. Russell discovered the Russell paradox (see below), introduced the theory of types, and popularized first-order predicate calculus. Russell’s logic consisted of two main ideas: that all mathematical truths can be translated into logical truths (or that the vocabulary of mathematics constitutes a proper subset of the vocabulary of logic) and that all mathematical proofs can be recast as logical proofs (or that the theorems of mathematics constitute a proper subset logical theorems).

Whitehead excelled not only in mathematics and logic, but also in the philosophy of science and study of metaphysics. In mathematics, he extended the known range of algebraic procedures, and he was a prolific writer. In philosophy, he criticized the traditional theories for their lack of integrating the direct relationship between matter, space, and time; thus he created a vocabulary of his own design, which he called the “philosophy of organism.”

Who was Kurt Gödel?

For about a hundred years, mathematicians like Bertrand Russell were trying to present axioms that would define the entire field of mathematics on an axiomatic basis. Austrian-American mathematician and logician Kurt Gödel (1906–1978) was the first to suggest that any formal system strong enough to include the laws of mathematics is either incomplete or inconsistent; this was called “Gödel’s incompleteness theorem.” Thus, axioms could not define all of mathematics.

What was Bertrand Russell’s “great paradox”?

In the early 1900s, Bertrand Russell discovered what is known as the “great paradox” as it applies to the set of all sets: The set either contains itself or it does not, but if it does, then it does not, and vice versa. The reason that this paradox became so important was its affect on mathematics. It created problems for those people who tried to base mathematics on logic, and it also indicated that something was wrong with Georg Cantor’s intuitive set theory, which at that time was one of the backbones of set theory. (For more about Russell and set theory, see “Foundations of Mathematics.”)

Gödel also stated that the various branches of mathematics are based in part on propositions that are not provable within the system itself, although they may be proved by means of logical (metamathematical) systems external to mathematics. In other words, nothing is as simple as it seems; and, interestingly enough, Gödel’s idea also implies that a computer can never be programmed to answer all mathematical questions.

What did David Hilbert propose in 1900?

In 1900, German mathematician David Hilbert (1862–1943) proposed 23 unsolved mathematical problems for the new century, most of which only proved to bring up other problems. By the 1920s, Hilbert gathered many mathematicians—called the formalists—to prove that mathematics was consistent. But all did not go well as mathematical complications set in. By 1931, Kurt Gödel’s incompleteness theorem dashed any more efforts by the formalists by proving that mathematics is either inconsistent or incomplete. (For more about Hilbert, see “Foundations of Mathematics.”)

What was the “Golden Age of Logic”?

Kurt Gödel’s work led to what is often described as the Golden Age of Logic. Spanning the years from about 1930 to the late 1970s, it was a time when there was a great deal of work done in mathematical logic. From the beginning, mathematicians broke into many camps, working on various phases of logic (for more information about logic, see “Foundations of Mathematics”), including:

Proof theory—In which the mathematical proofs started by Aristotle and continued by Boole (see above) were extensively studied, resulting in branches of this mathematics being applied to computing (including artificial intelligence).

Model theory—In which mathematicians investigated the connection between the truth in a mathematical structure and propositions about that structure.

Set theory—In which a breakthrough in 1963 showed that certain mathematical statements were undeterminable, a direct challenge to the major set theories of the time. This showed that Cantor’s Continuum Hypothesis (see above) is independent of the axioms of set theory, or that there are two mathematical possibilities: one that says the continuum hypothesis is true, one that says it is false.

Computability theory—In which mathematicians worked out the abstract theorems that would eventually help lead to computer technology. For example, English mathematician Alan Turing proved an abstract theorem that established the theoretical possibility of a single computing machine programmed to complete any computation. (For more information about Turing and computers, see below and “Math in Computing.”)

When was quantum mechanics developed?

There was not one major year in which quantum mechanics developed, or even one major scientist who proposed the idea. This modern physics theory evolved over about thirty years, with many scientists contributing to it. Beginning about 1900, Max Planck proposed that energies of any harmonic oscillator (such as the atoms of a black body radiator) are restricted to certain values. Mathematics came into play here, too, with each value an integral multiple of a basic, minimum value. Planck developed the equation E = hv (or “nu”), in which E (the energy of the basic quantum) is directly proportional to the v (the frequency of the oscillator) multiplied by h, or Planck’s constant (6.63 × 10^-34joule-second).

From there, mainly with the use of rigorous mathematics, others expanded or added to Planck’s idea, including German scientist Albert Einstein (1879–1955), who explained the photoelectric effect; New Zealand-born British physicist Ernest Rutherford (1871–1937) and Danish physicist Neils Bohr (1885–1962), who explained both atomic structure and spectra; Austrian physicist Erwin Schrödinger (1887–1961), who developed wave mechanics; and German physicist Werner Karl Heisenberg (1901–1976), who discovered the uncertainty principle. Out of these studies came quantum mechanics (in the 1920s), quantum statistics, and quantum field theory. Today, quantum mechanics and Einstein’s theory of relativity form the foundation of modern physics. These theories continually change or are modified as we get closer to understanding more about the physics—and mathematics—of our universe.

Who was Alan Turing?

British mathematician Alan Mathison Turing (1912–1954) was the first to propose the idea of a simple computer. Called the Turing machine, its operation was limited to reading and writing symbols on tape, moving the tape to the left or right to read the symbols one at a time. This is often considered the start of our computer age. In fact, the definition of the word “computable” is a problem that can be solved by a Turing machine. Turing was also instrumental in interpreting and deciphering encrypted German messages using the Enigma cipher machine. (For more information on computers, see “Math in Computing.”)

A statue of Alan Turing, inventor of the first simple computer, is located at the University of Surry in Guildford, England.

Who invented catastrophe theory?

Catastrophe theory—or the study of gradually changing forces that lead to so-called catastrophes (or abrupt changes)—was popularized by French mathematician René Thom (1923–2002) in 1972. Unable to use differential calculus in certain situations, Thom used other mathematical treatments of continuous action to produce a discontinuous result. Although it is not as popular as it once was, it is often used in biological and optical applications. (Note that this term is often used in geology, too—but don’t confuse them. Some 18th-century scientists once believed that geologic features were created by sudden and violent events, such as earthquakes and volcanic eruptions. Today, most geologists think Earth’s features form slowly, punctuated by the occasional catastrophic event.)

What is chaos theory?

Chaos theory is one of the “newest” ideas in mathematics. Developed in the last half of the 20th century, it affects not only math, but physics, geology, biology, meteorology, and many other fields. Modern ideas about chaos began when theorists in various scientific disciplines started to question the linear analysis used in classical applied mathematics, most of which presumes an orderly periodicity that rarely occurs in nature. In the search to discover regularities, the idea of disorder had been ignored. To overcome this problem, chaos theorists developed deterministic, nonlinear dynamic models that explain irregular, unpredictable behavior. By 1961, American meteorologist Edward Norton Lorenz (1917–2008) noticed that small variations in the initial values of variables in his primitive computer weather model resulted in major divergent weather patterns. His discovery of a simple mathematical system with chaotic behavior led to the new mathematics of chaos theory.

Why is mathematics never offered as a Nobel Prize?

The Nobel Prizes were established at the bequest of Swedish chemical engineer Alfred Bernhard Nobel (1833–1896), the discoverer of dynamite. First awarded in 1901, the Nobel Prizes honor the fields of chemistry, physics, physiology or medicine, literature, and peace; a prize in economics was added in 1969, but there is not an award for mathematics.

The lack of a mathematics prize has many stories attached, including one that states Nobel’s wife jilted him for Norwegian mathematician Magnus Gosta Mittag-Leffler, a notion made implausible by the fact that Nobel never married. Most historians agree, however, that the reason has to do with Nobel’s attitude toward mathematics: He simply did not consider mathematics sufficiently practical.

The use of chaos theory has enabled scientists and mathematicians to reveal the structure in aperiodic, unpredictable dynamic systems. For example, it has been used to examine crystal growth, the expansion of pollution plumes in water and in the air, and even to determine the formation of storm clouds. One of the reasons chaos theory has come to the forefront of science and mathematics is because of advancements in computers; high-end computers allow for a plethora of variables to enter into the complex chaos equations.

Who was Benoit Mandelbrot?

Benoit B. Mandelbrot (1924–2010) was the Polish-born French mathematician who invented a branch of mathematics called fractal geometry, which is designed to find order in apparently erratic shapes and processes. As a pioneer of chaos theory, he developed and found applications for fractal geometry—and all this as a largely self-taught mathematician who did not like pure logical analysis. Unlike traditional geometry with its regular shapes and whole-number dimensions, fractal geometry uses shapes found in nature with non-integer (or fractal, thus the name) dimensions. For example, twigs, tree branches, river systems, and shorelines can be examined using fractals. Today, fractals are often applied not only to the natural world, but to the chemical industry, computer graphics, and even the stock market.

Who is Grigori Perelman?

Grigori Yakovlevich Perelman (1966-, sometimes seen as Grisha Perelman) is a Russian mathematician who has made great contributions to Riemannian geometry and geometric topology. He also is credited with solving the Poincaré conjecture, a topological problem posed in 1904; he may have also proven Thurston’s geometrization conjecture. Some sources say he no longer practices mathematics. He has been offered several mathematical awards in the past, which he turned down; one was the Clay Millennium Prize for the resolution of the Poincaré conjecture, but he cited American Richard Hamilton’s contribution, a mathematician who suggested a program for the conjecture’s solution.

What are some major modern mathematical awards?

Contrary to the Nobel Prize bypass of mathematics, there are still some prestigious mathematical award-winning ceremonies. One of the oldest is the Fields Medal of the International Mathematical Congress, established in 1932. It has the equivalent prestige of the Nobel with the limitation that it is only awarded for work done by mathematicians younger than 40 years old, and the monetary value is a mere $15,000 in Canadian dollars (or about $14,715 in U.S. dollars at press time).

There are other more recent mathematical awards, too. In 1981, the Rolf Nevanlinna Prize was established, for the mathematical aspects of information science. It was named in honor of former president of the International Mathematical Union, mathematician Rolf Nevanlinna (1895–1980); the medal and cash prize is awarded every four years. In 2003, Norway created the Abel Prize for mathematical achievement. Named after Norwegian mathematician Niels Henrik Abel (1802–1829), who proved that solving fifth-degree algebraic equations (quintics) is impossible, the award gives the winner a prize of six million Norwegian kroners (at this writing, about $1,036,000 in American currency).

Another award is the Chern Metal Award, in memory of Chinese mathematician Shiing-Shen Chern (1911–2004), which was first awarded in 2010; it is given every four years on the occasion of the International Congress of Mathematicians. The cash prize of $250,000 U.S. dollars is awarded to any individual—regardless of age or vocation—for outstanding achievements in mathematics. The Carl Friedrich Gauss Prize for Applications in Mathematics, first awarded in 2006, is to honor scientists whose mathematical research has contributed toward technology, business, or in people’s everyday lives—in other words, has had an impact outside of mathematics. (For more information about Gauss, see elsewhere in this chapter, and “Math Basics.”)