The Handy Math Answer Book, Second Edition (2012)

MATH BASICS

BASIC ARITHMETIC

What is arithmetic?

Arithmetic is a branch of mathematics that deals with numerical computation— specifically computation using integers, rational numbers, real numbers, or complex numbers—with the computations simple to complex. The word arithmetic has its roots in the Greek word for “to count” (arithmeein; also arithmos, or “number”).

Arithmetic contains all the rules for combining two or more numbers. In most cases, when mathematicians talk about elementary arithmetic, they are speaking of those subjects most of us learned in grade school: addition, subtraction, multiplication, and division being the most common; and fractions, geometry and measurements, ratios and proportion, simple probabilities, and algebra examined in more advanced levels. For even more advanced students, such arithmetic lessons as congruence calculation, root extraction, power computations, and advanced factorizations are often presented.

Are there more advanced concepts in arithmetic?

Yes, arithmetic can even be more advanced than the ideas mentioned above. For example, higher arithmetic is the archaic term for number theory, which is the study of the properties of integers, or whole numbers (0, ± 1, ± 2…). It can include simpler arithmetic concepts to more complex, such as diophantine equations (for more information about these equations, see “Algebra”), prime numbers (see below), and functions such as the Riemann hypothesis (for more about Friedrich Bernhard Riemann, see “History of Mathematics” and “Geometry and Trigonometry”).

There are other more advanced ideas in arithmetic, too. For example, modular arithmetic is known as the arithmetic of congruences (see below). The model theory discusses the existence of “non-standard” models of arithmetic. And floating-point arithmetic is performed on real numbers by computers or other automated devices.

When was the first arithmetic book published in North America?

In 1556 the first arithmetic book was published in North America by Brother Juan Diez Freyle, a Franciscan friar. The name of the book was Sumario compendioso de las quentas de plata y oro que in los reynos del Piru son necessarias a los mercaderes y todo genero de tratantes: Con algunas reglas tocantes al Arithmética. The title translates to Comprehensive summary of the counting of silver and gold, which, in the kingdoms of Peru, are necessary for merchants and all kinds of traders. The book explained the conversion of gold ore into value equivalents in different types of coinage in the Old World, problems that required the use of ratios and proportions. Diez also included a short chapter on algebra.

The first English language mathematics book written in North America was published in 1729 by Isaac Greenwood and titled Arithmetik, Vulgar and Decimal (“vulgar” refers to the common people). Greenwood’s life was also somewhat vulgar: He was appointed to the first Hollis Professorship of Mathematics and Natural Philosophy at Harvard University in Massachusetts when it was founded in 1727. By 1737, he was removed for “intemperance.” Reportedly, he drank too much, and more than likely, his views, philosophical and otherwise, differed greatly from those of his colleagues at the university.

What is arithmetic progression?

Arithmetic progression is one of the simpler types of series in mathematics. It is usually in the form of a, a + d, a + 2d, a + 3d, and so on, in which a is the first term and d is the constant difference between the two successive terms. A progression is also seen as these numbers are added, as in a + (a + d) + (a + 2d) + (a + 3d) +,…, (a + [n + 1]d). An example of an arithmetic progression would be 2 + 6 + 10 + 14 + …, in which d is equal to 4.

What do computers and arithmetic have in common?

Computers and arithmetic have a great deal in common. Arithmetical operations are actually digital computer operations in which the numerical quantities are computed, either through adding, subtracting, multiplying, dividing, or otherwise comparing. Arithmetical instructions give a computer program direction to perform an arithmetic operation on specific types of data, such as addition, subtraction, multiplication, and division. The sections of the computer that carry out these computations and other logic operations are called arithmetical units (or arithmetic sections). (For more information about computers and math, see “Math in Computing.”)

ALL ABOUT NUMBERS

What is a number?

The term number can be defined in many ways, including a sizable collection of people or things, and even an indefinite quantity or collection. In mathematics, a number, or numeral, is usually defined as a symbolic representation of a specific quantity or place in a sequence; to most people, the most familiar numbers are 1, 2, 3, 4, 5, and so on.

Computers have become such an everyday part of our lives that we hardly think about them. Yet the mathematical concepts that lie behind their operations are staggering.

What is a decimal system?

The decimal system uses the base 10 notation system to represent real numbers. A decimal expansion is the expression of a number within the decimal system, such as 1, 15, 359, 18.7, and 3.14159. Each number within the system is called a decimal digit. (Such decimal notation—or a numbering notation based on decimals—was first used in India around 594.) The decimal point is represented by a period placed to the right of a unit’s place in a decimal number. It is interesting to note that a comma is used in continental Europe to denote a decimal point, such as 3,25 (translated as 3.25 as a decimal point), which in this case would logically be called the decimal comma.

What is currently the most common numeration system?

The most common numeration system in use today is the Hindu-Arabic. This set of numerals has ten digits in a place value decimal system, which is a fancy way of saying that a decimal system—one based on tens—is an integral part of the system and that each number has a certain value depending on its place in the list of numbers.

How did the Hindu-Arabic numerals spread to Europe?

Hindu-Arabic numerals (often less accurately called Arabic numerals or numbers) had their roots in India before 300 B.C.E. From there, the use of Indian numerals followed the more western trade routes to Spain and Northern Africa that were taken by the Arabic/Islamic peoples; this consequently resulted in the expanded use of these symbols.

One of the earliest and most common devices developed for making everyday calculations was the abacus, which was still being used in Europe as late as the 15th century.

It took several more centuries for the idea to spread to Europe. Although the Spanish used some Hindu-Arabic symbols as early as the late 900s, records of a more extensive use of these symbols occurred around 1202. Italian mathematician Leonard of Pisa (also known as Fibonacci, c. 1170-c. 1250; for more about Fibonacci, see elsewhere in this chapter, and also in “History of Mathematics” and “Mathematics throughout History”) introduced the Hindu-Arabic numbers in his book Liber Abaci (The Book of the Abacus). The acceptance of such a numbering system was difficult. For example, in some places in Italy, it was forbidden to use anything but Roman numerals. By the late 15th century, most people in Europe were still using an abacus and Roman numerals.

The 16th century was the turning point, with European traders, surveyors, bookkeepers, and merchants spreading the use of the Hindu-Arabic numerals. After all, it took longer to record data using Roman numerals than with Hindu-Arabic numbers. The advent of the printing press also helped by standardizing the way the Hindu-Arabic numbers looked. By the 18th century, the “new” numeration system was entrenched, establishing a system that dominates the way we work with and perceive numbers in the 21st century. (For more information about Hindu-Arabic and Roman numerals, see “History of Mathematics.”)

How did the Hindu-Arabic numbers evolve?

The evolution of the Hindu-Arabic numbers was not a straight line from India to Arabia and on to Europe. In between, the Arab cultures had more than one number system to contend with, including at least three different types of arithmetic: finger-reckoning arithmetic (counting on fingers), a sexagesimal system with numbers written in letters of the Arabic alphabet, and Indian numeral arithmetic.

The evolution of the Hindu-Arabic numbers continued throughout time and includes some good reasons for why our numbers look as they do today. For example, historians believe that between 970 and 1082, the numbers 2 and 3 changed significantly, rotating 90 degrees from their original written position. This is thought to be due to how scribes worked: Sitting cross-legged, they wrote on a scroll they wound from right to left across their body. This caused them to write from top to bottom, not our usual right to left; the script was then rotated when the scroll was read.

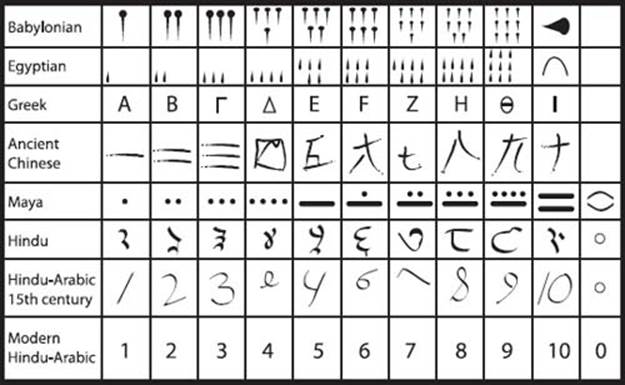
Different cultures generally employed one of two strategies when creating symbols for numbers: multiple marks that indicated single numbers or multiples of fives or tens (e.g., Babylonian, Egyptian, Mayan), or a more abstract system using a single symbol for the numbers one through nine, with numbers then being shifted over one or more places to indicate multiples of ten, hundreds, etc. (e.g., Hindu, Hindu-Arabic).

What do integers include?

Integers include the whole numbers (also called positive integers or natural numbers), negative whole numbers (also called negative integers or the negatives of the naturals), and zero. Numbers such as 3/4, 5.993, 6.2, -3.2, and pi (π ; or 3.14 …) are not considered integers. Only integers are used when speaking of odd and even numbers (zero is considered to be an even number; for more about zero, see below).

How are numbers classified?

The set of natural numbers are also called integers—or counting or whole numbers— which are usually defined as the positive and negative whole numbers, along with zero (0). But many times, mathematicians do not use the term “natural numbers,” and instead define numbers based on the following terminology and/or symbols:

What is a place value?

The place value, or “rule of position,” are numbers whose value depends on the place or position they occupy in a written numerical expression. In the Hindu-Arabic counting system, the numerals 1, 2, 3, 4, 5, 6, 7, 8, 9, and 0 have certain specific place values. For example, the number 7 represents 7 (7 units), 70 (as 7 tens), 700 (as 7 hundreds), and so on—the 7’s values based on their position in the numerical expression. (For more information about place values, see “History of Mathematics.”)

What are some of the highest numbers we know?

Numbers can go on forever—in other words, there are an infinite number of numbers— so no one will ever reach the “highest number.” The highest numbers with which we are most familiar (and can comprehend) include million, billion, and trillion, often referring to such quantities as the number of miles to the outer planets or the federal budget deficit. These larger numbers are usually separated by comma at the thousands, millions, trillions, etc. place values. For example, for 3,490, the comma is after the thousand place value; for 1,384,993, after the million and thousand place value. Larger numbers written for technical papers are sometimes expressed with spaces; for example, 11 384 443 is equivalent to 11,384,443.

What are the various scales used by countries to label big numbers?

Not every country labels the highest numbers in the same way. Depending on the country, they use either the short scale or the long scale. The short scale is taught in American school systems, thus it is thought to be used exclusively in the United States. Other countries, including most of continental Europe, use the long scale. And several countries, including China, have large number naming systems that are even different than the long and short scales.

For example, in the American system, denominations above 1,000 million (or the American billion) are 1,000 times the preceding one (for example, one trillion is 1,000 billion; one quadrillion is 1,000 trillion). In the British system, the first denomination above 1,000 milliards (the British billion) is 1,000,000 times the preceding one (for example, one trillion is 1,000,000 billion; one quadrillion is 1,000,000 trillion). The American system is based on the French system, which the French ironically no longer follow. Their larger number names now correspond to the British system, as do those of many other countries in Europe.

American and British Naming Systems for Large Numbers

What are a googol and a googolplex?

The “googol” is the invention of Milton Sirotta, the eight-year-old nephew of mathematician Edward Kasner (1878–1955), who once asked the young boy to name the number 1 followed by 100 zeros (10 to the 100th power or 10¹⁰⁰). It is also seen as “10 duotrigintillion” on the short scale, and ten thousand sexdecillion on the long scale (for more about scales, see elsewhere in this chapter). Since a googol is an incredibly large number, there is little it can represent. Although one might think it would represent some collection of astronomical entities, such as the number of elementary particles in the universe, it does not. Scientists estimate only about 10 to the 80th power (10⁸⁰) such particles exist. Googol was soon followed by googolplex, a name thought to be invented by Kasner, and said to equal 10 to the power of googol (or 1 followed by 10 to the power of 100 zeros or one followed by a googol of zeros).

No one has ever seen such large numbers printed out. And although it is true that computer processing power doubles about every one to two years—and the use of computer networks across the Internet even faster—it is still too early to print the number represented by a googol or a googolplex. Thus, many ask why begin at all, since attempts to do so will soon be overtaken by faster processors? In fact, it is estimated that it will take another 500 years before such an endeavor is achieved—but with the advancement of computer processing, in ten years, the number of years will no doubt be even less.

What are non-vanishing and vanishing numbers?

A non-vanishing number is just as the term implies: A quantity that is non-zero everywhere. For example, in the expression x⁴ + 1, the answer will never be zero (even when x is zero or a negative number). The answer for the expression x² is called “vanishing” because if x = 0, the expression’s answer “vanishes” to zero.

What are rational, irrational, and real numbers?

Rational, or fractional, numbers are most often regarded as divisions (or ratios) of integers. By creating a fraction (dividing one integer by another), a rational number produces either a number that “ends” or repeats decimals. For example, 1/4 equals the decimal equivalent of 0.25; 1/3 is equivalent to 0.33333 … Both of these are rational numbers. (For more information about fractions, see below.)

On the other hand, irrational numbers are all the numbers that can be written as non-repeating, non-finite (or non-terminating) decimals. Also called non-rational numbers, they include the decimal equivalent of pi (or 3.141592 …). Finally, if you put the rational and irrational numbers together, they form the real numbers. Most numbers we use in our everyday lives are real numbers.

What are imaginary numbers?

The “opposite” of real numbers are (logically enough) called imaginary numbers. In particular, they are all non-zero multiples (real numbers) of the square root of -1, also called i, with the formula defined as follows:

The does not have a position on a number line; and no number can be squared to get -1. (If you square a positive number, the result is positive; if you square a negative number, the result is also a positive number.) Thus, in order to square a number to get a negative one, mathematicians invented the imaginary number i.

Can there be more than one type of number?

Yes, numbers can be classified as more than one type, and it’s not always easy to keep them straight. The following lists some ways to better understand the plethora of number types:

· A rational number is not always an integer: 4/1 is an integer, but 2/3 is not; but an integer is always a rational number—because it can be represented by a fraction by putting the integer over 1, or /1, such as 2/1 or 234/1.

· A number can either be rational or irrational but not both.

· The number for pi (3.141592…) is irrational (the decimal does not repeat) and real.

· 0.25 is considered rational (the numbers terminate) and real.

· The fraction 5/3 is rational (it’s a fraction) and real.

· The number 10 can be explained using many terms, including a counting number, whole number, integer, rational, and real.

How do regular and non-regular numbers differ?

Regular and non-regular numbers are actually other terms for rational numbers. Regular numbers are positive integers that have a finite decimal expansion. In other words, a number that seems to “end.” For example, one quarter (1/4) is equal to the decimal equivalent of 0.25, in which the numbers end with the “5.” A non-regular number is one that includes repeating decimals—numbers that seem to go on forever. For example, one third (1/3) is equal to the decimal equivalent of 0.3333…, in which the number 3s go on indefinitely.

Who uses complex—thus imaginary—numbers?

Complex (and thus imaginary) numbers are used by many people in various fields. The most logical is in the field of mathematics: In algebra, complex numbers give mathematicians a way to find the roots of polynomials.

Engineers and scientists also often need to use complex numbers. Because such applications are based on polynomial models in theory, complex numbers are needed. For example, circuit theory has polynomials as part of the model equation for simple circuits. Vibrations with wavelike results in mechanical engineering are also connected to the use of complex numbers. And even in physics, quantum mechanics uses complex numbers for just about everything. The wave functions of particles that have a complex amplitude include real and “imaginary” parts—both of which are essential to the computations.

Complex numbers are also used by musicians, economists, and stockbrokers as well. And indirectly, everyone who has to deal with light switches, loudspeakers, electric motors, and sundry other mechanical devices uses imaginary numbers just by using things that were engineeredthrough the use of imaginary numbers.

How do you perform imaginary numbers computations?

Imaginary numbers come in handy to do many computations, especially something called simplification. Here are some “simple” examples of how to use imaginary numbers:

To simplify the square root (or sqrt) of -25:

To simplify 2i + 4i:

To simplify 21i - 5i:

To multiply and simplify (2i)(4i):

(2i)(4i) = (2 × 4)(ii) = (8)(i²) = (8)(-1) = -8

Who first came up with the idea of imaginary numbers?

The origin of i is difficult to trace. Some historians give credit to Italian physician and mathematician Girolamo Cardano (1501-1576; in English, known as Jerome Cardan). In 1545, he is said to have started modern mathematics, first mentioning not only negative numbers but imaginary numbers in his Latin treatise, Ars Magna (The Great Art). But Cardano did not consider the imaginary numbers as the real mathematical objects we do today. To him, they were merely convenient “fiction” to classify certain polynomial properties, describing how their roots would behave when he pretended they even had roots.

Eighteenth-century Swiss mathematician Leonhard Euler, who published over 70 volumes on mathematics in his lifetime, was one of the greatest contributors to the discipline that ever lived. Euler developed important concepts in such areas as geometry, calculus, trigonometry, algebra, hydrodynamics, and much more. He also created the concept of the imaginary number that is the square root of —1

Most agree that around 1777, Swiss mathematician Leonhard Euler (1707–1783) used “i” and “-i” (negative i) for the two different square roots of -1, thus eliminating some of the problems associated with notation when putting polynomials into categories. (He is also credited with originating the notation a + bi for complex numbers.) Much to the consternation of many past and present mathematicians, i and -i were called “imaginary,” mainly because the number’s function at the time of Euler was not clearly understood. When German mathematician, physicist, and astronomer Johann Friedrich Carl Gauss (1777–1855) used them for the geometric interpretation of complex numbers as points in a plane, the usefulness of imaginary numbers became apparent. (For more information or Gauss, Cardano, and Euler, see “History of Mathematics.”)

What are complex numbers?

Complex numbers have two parts: the “real” part (any real number) and an “imaginary” part (any number with an i in it). The standard complex number format is “a + bi,” or a real number plus an imaginary number. It is also often seen as x + iy, because while real numbers are viewed on a line, complex numbers are viewed graphically on an Argand (or polar) coordinate system: The imaginary numbers make up the vertical (or y) axis as iy, while the horizontal (or x) axis is occupied by real numbers. (For more information about coordinate systems, see “Geometry and Trigonometry.”)

What is the polar form of a complex number?

The polar form of a complex number is equal to a real number expressed as a angle’s cosine, and the imaginary number (i) times the same angle’s sine, with the angle expressed in radians (for more about angles, sines, cosines, and polar forms, see “Geometry and Trigonometry”). This is seen in equation form as: r(cos θ + i sin θ), in which r is the radius vector, θ is the angle, and i is the imaginary number.

Is there such a thing as a perfect number?

Yes, there is such a thing as a perfect number, but it is not what we think of as true perfection. To mathematicians, perfect numbers are somewhat rare because they are few and far between. They are defined as a natural number (or positive integer) in which the sum of its positive divisors (or the bottom number in a fraction that divides the number to equal another whole number, and includes 1 but not the number itself) is the number itself. For example, 6 is considered a perfect number because its divisors are 1, 2, and 3—or 1 + 2 + 3 = 6. The next perfect numbers are 28 (1 + 2 + 4 + 7 + 14), 496, 8128, 33550336, 8589869056, 137438691328,2305843008139952128, and so on—with larger and larger perfect numbers being discovered, especially with the help of faster and more memory-packed computers. (For more about perfect numbers, see Mersenne primes, elsewhere in this chapter.)

What is meant by one-to-one correspondence?

A one-to-one correspondence means as the words imply: that the number of objects, numbers, or whatever is the same as the set of other objects, numbers, or whatever. (In set theory, the one-to-one correspondence means something different; for more about set theory, see “Foundations of Mathematics.”)

Everyone has no doubt had contact with one-to-one correspondence without even thinking about it. For example, there is a one-to-one correspondence of the number 10 to the number of fingers on both hands (ten). Counting a deck of cards is a one-to-one correspondence—each number, from 1 to 52, representing a card in the deck. When you compare two decks of cards, putting the cards side-by-side to equal 52 in each deck, this could also be considered a one-to-one correspondence.

Not everything is counted in such a way. For example, when mathematicians want to know the size of an unknown quantity, they put the unknown quantity in a one-to-one correspondence with a known quantity.

Do numbers continue to infinity?

When most of us think of infinity, we envision the universe continuing on forever; and in mathematics, we often think of numbers that are never-ending. Sometimes it is difficult to understand infinity since our own lives—and most of our experiences—are finite (eventually end). Infinity is a mind-boggling concept.

There are several rules to mathematical infinity—the three most important are: no matter how high you count numbers, you can always count higher; no matter what length you draw parallel lines, they will never meet; and when starting with a line, dividing it in half, then dividing that in half, and so on, you will never stop dividing the resulting line segment.

Even though scientists and mathematicians agree that infinity exists theoretically, it is often a difficult concept to understand and accept. Is it true that the number of particles in the universe are infinite? Does the universe continue on forever? Do parallel lines eventually meet at a place we have yet to discover? If a particle is infinitely divided, just how small can an atomic particle become? And to add to the unimaginable explanations, German mathematician George (Georg) Ferdinand Ludwig Philipp Cantor (1845–1918) mathematically reasoned out that not only do infinities come in different sizes, but there are an infinite number of infinities.

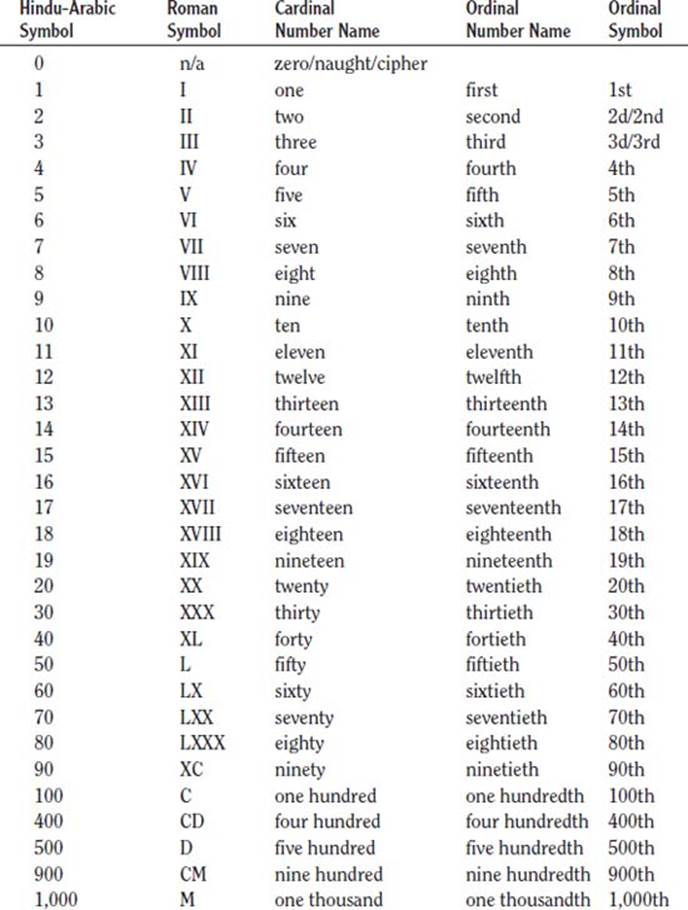
What are ordinal and cardinal numbers?

In common arithmetic terms, cardinal numbers are those that express amounts; they are also used in simple counting or to answer the question of quantity (how many). They can be nouns (try counting to ten); as pronouns (ten were discovered); or adjectives (ten cats). Specifically, the term is from the Latin cardin, meaning “stem” or “hinge,” thus meaning the most important or principal numbers with others depending (hinging) on those numbers. We are most familiar with the cardinal numbers as our counting numbers or the Hindu-Arabic numeration system—1, 2, 3, and so on.

Ordinal numbers are much different. In common, arithmetic terms, ordinal numbers are adjectives that describe the numerical position of an object, such as first, second, third, and so on. They are used to show the order of succession for objects (second chair), names (second month), or periods of time (2nd century).

Note that cardinal and ordinal numbers are easily divided. For example, in the Hindu-Arabic numeration system, the cardinal numbers may be read as ordinals, such as May 10 being read as “May tenth.” Such differences are even harder to distinguish when it comes to Roman numerals. Most of the time, these numerals are considered cardinal numbers (I, II, III, etc.), but they can also be ordinal numbers in certain contents, such as Henry the VIII (Henry the Eighth). Roman numerals can even contain ordinal suffixes, such as the IXth Dynasty.

Ordinal and Cardinal Numbers and Symbols

Why are the terms cardinal and ordinal sometimes confused in mathematics?

Cardinal and ordinal numbers are sometimes confused because they have two distinct mathematical definitions. The cardinal numbers in the numbering system should not be confused with cardinal numbers in set theory, in which any method of counting sets using a cardinal number gives the same result. Likewise, the ordinal numbers in arithmetic should also not be confused with ordinal numbers in set theory: Such numbers, often called ordinals for short, are the order type of a well ordered set. They are divided into two types: finite and transfinite ordinals. (For more about sets, ordinals, and cardinal numbers, see “Foundations of Mathematics.”)

MORE ABOUT NUMBERS

What is congruence?

In reference to numbers, congruence is the property of two integers having the same remainder upon division by another integer. The term also is often used in geometry to describe a property of geometric formations (for more information about congruence in geometry, see “Geometry and Trigonometry”). Still another way of using congruence is in number theory, in which modular arithmetic is the arithmetic of congruences, which is sometimes informally called “clock arithmetic.”

How does modular arithmetic work?

In modular arithmetic, numbers “wrap around” when they reach a fixed quantity. This is also called the modulus—thus the name modular arithmetic—with the standard way of writing the form as “mod 12” or “mod 2.”

In this case, if the two numbers b (also called the base) and c (also called the remainder) are subtracted (b - c), and their difference is a number integrally divisible by m, or (b - c)/m, then b and c are said to be congruent modulo m. Mathematically, “b is congruent to c (modulo m)” is written as follows, with the symbol for congruence (≡):

b ≡ c (mod m)

But if b - c is not integrally divisible by m, then it is said, “b is not congruent to c (modulo m),” or

b ≢ c (mod m)

More formally, modular arithmetic includes any “non-trivial homomorphic image of the ring of integers.” We can interpret this interesting definition using a clock. The modulus would be the number 12 on the clock (arithmetic modulo 12), with an associated ring labeled C₁₂ and the allowable numbers being 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, and 11. Another example is arithmetic modulo 2, with an associated ring of C₂, or allowable numbers of 1 and 2.

What is the Fibonacci sequence?

We can look to the familiar face of a clock to illustrate the concept of “clock arithmetic” or modulo 12. With clocks, we can count through 11 before getting to 12, where we start over again at zero. Thus, if it is 7 o’clock and we add 6 hours, we get 1 o’clock, not 13 o’clock.

Italian mathematician Leonard of Pisa (c. 1170-c. 1250; also known as Fibonacci, or “son of Bonacci,” although some historians say there is no evidence that he or his contemporaries ever used the name) may be known for helping to introduce Hindu-Arabic numerals to Europe (for more information about Fibonacci and numerals, see elsewhere in this chapter), but he also is famous for the sequence of numbers he discovered. This sequence—initially pursued as an exercise to determine how fast a pair of rabbits can reproduce per year—is formed by adding the two preceding numbers to find the next number, starting with a pair of ones. Thus, the Fibonacci numbers in this sequence are 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, and so on; or

1 + 1 = 2

2 + 1 = 3

3 + 2 = 5

5 + 3 = 8

8 + 5 = 13

13 + 8 = 21

21 + 13 = 34

34 + 21 = 55

55 + 34 = 89

89 + 55 = 144

144 + 89 = 233

233 + 144 = 377, and so on.

What are prime and composite numbers?

There are many definitions of prime numbers—and they all mean the same thing in translation. For example, prime numbers are defined as positive integers (natural numbers) that are greater than 1 and have only 1 and the prime number as divisors (factors). Another definition is an integer greater than 1, in which its only positive divisors are 1 and itself. Still yet another definition is that a prime is a natural number that has exactly two distinct natural number divisors, 1 and itself. For instance, the prime numbers less than 20 are 2, 3, 5, 7, 11, 13, 17, and 19. All other integers greater than 1 that are not prime numbers are called composite numbers.

What are some examples of “clock arithmetic”?

As stated above, the clock would be considered arithmetic modulo, with calculations including such statements shown below (Note: In all of the first calculations, the equal sign can be replaced with the congruence sign =, or three lines instead of the two for an equal sign.):

11 + 1 = 0, also written as 11 + 1 = 0 (mod 12)

7 + 8 = 3, also written as 7 + 8 = 3 (mod 12)

5 × 7 = 11, also written as 5 × 7 = 11 (mod 12)

There are other rules concerning prime and composite numbers. The number 1 is unique, and is not considered a prime or composite number. And one of the basic theorems of arithmetic is that any positive integer is either a prime or the product of a unique set of prime numbers. For example, the number 12 is not a prime, but it has a unique “prime calculation” written as: 2 × 2 × 3.

What is the Sieve of Eratosthenes?

The smallest prime numbers—those less than 1 million—can be determined using something invented circa 240 B.C.E.: the Sieve of Eratosthenes (note: the largest primes are found using Lagrange’s Theorem from group theory studies). This method was named after astronomer and mathematician Eratosthenes of Cyrene (276-196 B.C.E.), who was actually more famous for calculating the circumference of the Earth than for his work with prime numbers.

To determine primes using this method, make a list of all the integers less than or equal to n (numbers greater than 1) and get rid of all the multiples of all primes less than or equal to the square root of n. The numbers that are left are all primes. For example, to determine primes less than 100, start with 2 as the first prime; then write all odd numbers from 3 to 100 (there is no need to write the even numbers). Take 3 as the first prime and cross out all its multiples in the numbers you listed. Take the next number, 5, and then 7, and cross out all their multiples. By the time you reach 11, many numbers will be eliminated and you will have reached a number greater than the square root of 100 (11 is greater than 10, the square root of 100). Thus, all the numbers you have left will be primes.

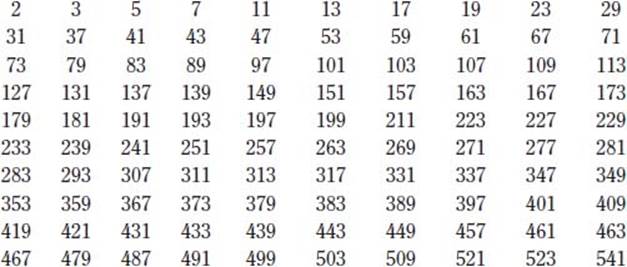
What are the first 100 prime numbers?

The first 100 prime numbers are as follows:

What is the Reimann zeta-function?

German mathematician Georg Friedrich Bernhard Riemann (1826–1866) was responsible for the Riemann zeta-function—the master of all the L-functions that would reveal how the prime numbers are distributed. (There are two types of L-functions— algebraic and transcendental—classified according to their degree, including the zetafunction.) Involved in all of this is the Riemann Hypothesis, an important unsolved mathematical problem. The Riemann Hypothesis is an example of something that should be true for every L-function. In 2008, researchers exhibited the first example of a third degree transcendental L-function—with the researchers’ studies showing that some conditions could be confirmed in the Riemann Hypothesis. Now scientists hope these L-functions will help interpret many connections between different areas of mathematics.

Are there different types of prime numbers?

Yes, there are different types of prime numbers, including the following:

· Mersenne primes—See below for an explanation.

· Twin primes—Primes of the form p and p + 2 (in other words, they differ by two); discovering such a prime involves finding two primes.

· Factoridl/primorialprimes—Primorial primes are of the form n# ± 1; factorial primes are of the form n! ± 1.

· Sophie Germain primes—This is an odd prime p for which 2p + 1 is also a prime. It was named after Sophie Germain (1776–1831), who proved that the first case of Fermat’s last theorem for exponents was divisible by such primes.

Other names for prime numbers are mainly for descriptive purposes. For example, in 1984, mathematician Samuel Yates defined a titanic prime to be any prime with at least one thousand digits. In the past few decades since his definition, there have been over a thousand times more such primes discovered. Yates also coined the term gigantic prime to indicate a prime with at least 10,000 digits. Thanks to advances in computer technology, a great deal of prime number generation has happened in the past decade, including surpassing 10,000 digits into the millions. To date, the largest prime number known was uncovered in 2009—a (Mersenne) prime number with 12,978,189 digits, written shorthand as 2 to the power of 43,112,609, minus 1. As to whether mathematicians will eventually find a one billion digit prime number, often referred to as a bevaprime, is no doubt only a matter of time.

What special number was recently factored?

In 2007, mathematicians from three institutions worked for eleven months to churn out the prime factors of a well-known, hard-to-factor number—which turned out to be 307 digits long. It was also called a “special number,” because it has a special mathematical form: close to a power of two. Mathematicians know it’s relatively easy to identify large prime numbers, but factoring (breaking down) a number into its prime components is very difficult. But the applications may be worth the time spent, especially for those people who work to safeguard our computer information with special encryption techniques. As for the next iteration to factor, scientists hope it won’t be long before this record is broken.

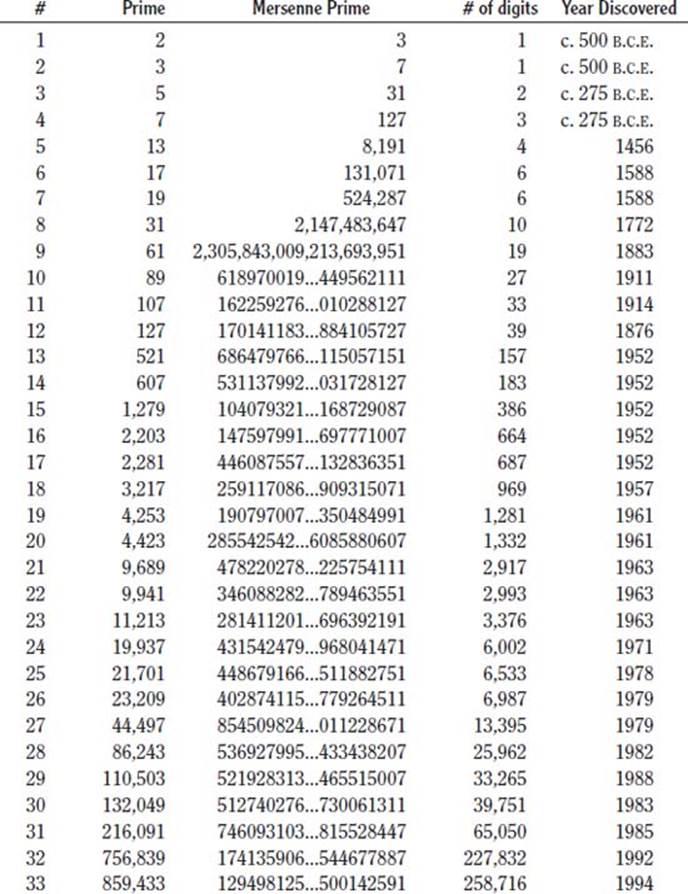
What is the story behind the Mersenne primes?

Mersenne primes (or Mersenne numbers) are connected to prime numbers. They are from the form 2^p - 1, in which p is a prime; or said another way, when 2^p - 1 is prime, it is said to be a Mersenne prime.

Centuries ago, many mathematicians believed that numbers from the form 2^p - 1 (they actually used the form 2ⁿ - 1, which is the same as the 2^p - 1 used today) were prime for all primes p. By the 16th century, it was proven that 2¹¹ - 1 = 2,047 was not prime. By 1603, Pietro Cataldi (1548–1626) correctly discovered that p = 17 and p = 19 were both prime, but he was wrong to add 23, 29, and 37 to his prime numbers list. Soon others discovered his errors, including French mathematician Pierre de Fermat (1601–1665) in 1640, and Swiss mathematician Leonhard Euler (1707–1783) in 1738.

The hunt for primes continued. The name “Mersenne” actually came from French priest, Father Marin Mersenne (1588–1648) who in 1644 referred to such numbers in the preface to his book Cogitata Physica-Mathematica. He believed that these special primes were: p = 2, 3, 5, 7, 13, 17, 19, 31, 67, 127, and 257. But like earlier attempts at determining prime numbers, many of Mersenne’s numbers were in error. It took three centuries more to check Mersenne’s range of numbers, and by 1947, the correct list of Mersenne primes were: p = 2, 3, 5, 7, 13, 17, 19, 31, 61, 89, 107 and 127. Interestingly enough, even though Mersenne incorrectly stated certain numbers belonged to this group—he probably didn’t verify all the numbers on his list—his name is still attached to the numbers.

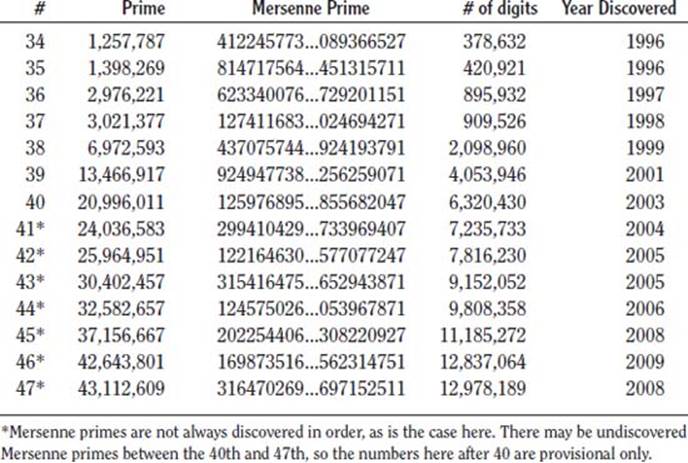
What is GIMPS?

GIMPS stands for the Great Internet Mersenne Prime Search, a program started in January 1996 to discover new world-record-sized Mersenne prime numbers. It harnesses the power of the Internet—and thousands of small computers belonging to public and private concerns.

This worldwide volunteer computing project made history in 2009, when the Electronic Frontier Foundation awarded GIMPS a $100,000 Cooperative Computing Award. The award was for the August 23, 2008 discovery of the 47th known Mersenne prime (M47). This huge 12,978,189 digit number was found on a University of California (Los Angeles) computer in the GIMPS PrimeNet network. So far, the GIMPS project has discovered thirteen Mersenne primes, with the latest—the 47th found by Odd Magnar Strindmo from Melhus, Norway—on April 12, 2009.

Not only do the volunteers with GIMPS search for the elusive record Mersenne primes, but it also is used to verify others found. For example, by July 2010, seven years after the 40th known Mersenne prime was discovered, GIMPS members double-checked all the smaller Mersenne primes, and found no other primes. Thus, the “40th known Mersenne prime” became the “40th Mersenne prime.”

The collaboration is still going on and, in fact, there are other awards for finding the various prime numbers. There are still two Cooperative Computing Awards up for grabs: the EFF award of $150,000 to the first person or group who discovered a prime with at least 100 million digits. Another is the CCA for discovering a prime with at least a billion digits, a prize worth $250,000.

GIMPS uses around 8 MB of memory and 10 MB of disk space per personal computer, and the computer should be on most of the time. If you decide to join the GIMPS group, be patient—a test can take a while to complete. To find out how you can get involved with GIMPS, get on your computer, log on to the Internet, and type http://www.mersenne.org/prime.htm into your browser. You’ll find directions for downloading the correct software right on the GIMPS site.

What hypothesis concerning prime numbers has finally been proven?

There are numerous hypotheses about prime numbers that have yet to be resolved. For example, since Euclid’s time, it’s been known that the sequence of prime numbers is infinite, but it is still unknown if an infinity of prime numbers p exists, such that p + 2 is also a prime number. And another one is that, on average, there are as many prime numbers for which the sum of decimal digits is even as prime numbers for which it is odd—or, more simply put, that the sum of digits of prime numbers is evenly distributed. This hypothesis was proposed by Russian mathematician Alexandre Gelfond in 1968, and now, it has been proven to be true. Why study such complex theories about prime numbers? Like many things in mathematics, such studies—besides being exciting to theoretical mathematicians—have important implications and applications in digital simulations and cryptography.

What are exponents?

Exponents are actually shorthand for multiplications, and represent the number of times a number is being multiplied—called the base. For example, (9) × (9) = 9², or 9 × 9 × 9 = 9³.

Another way to describe this process is called “raising to a power,” in which the exponent (a number as a superscript) is the “power.” For example, 9³ is “nine raised to the third power.” It is also easier to write larger numbers with exponents. For instance, instead of writing xxxx, we can write x⁴. (For more information about exponents, see “Algebra.”)

How can we simplify various expressions using exponents?

The following are ways to solve simple mathematical expressions with the same base:

To multiply two numbers with different exponents, add the exponents:
(x²)(x⁴) = (xx)(xxxx) = xxxxxx = x²⁺⁴ = x⁶

To raise a number with a power, multiply the exponents:
(x³)³ = (x³)(x³)(x³) = (xxx)(xxx)(xxx) = xxxxxxxxx = x^(3x3) = x⁹

What common mistake is often made in exponential equations?

Unlike multiplication, exponents do not “distribute” over addition. For example, (2 + 5)² does not mean 2² + 5² = 4 + 25 = 29. In this case, you add the numbers in the parentheses first, then square that number. The true answer to this equation is (2 + 5)² = 7² = 49.

What is a base in mathematics?

The term “base” has many meanings in the English language, including several that apply to the field of mathematics. When talking about sets, bases are the open sets whose union forms an abstract entity called a topological space. In geometry, the base represents the side of a polygon or polyhedron that is perceived as its bottom; when referring to an isosceles triangle, the base is the side that differs in length from the other two (thus, the base angles include the side that is thought of as the base). Algebraists also use the term base to describe either the number used with an exponent to create a power, such as 3⁴ = 81; or to write the same number as a subscript to a logarithm, such as log₃ 81 = 4. (For more information about logarithms, see “Algebra.”)

One of the more familiar uses of the term base in mathematics deals with our numbering system, in which a base is a natural number whose powers are added to produce a specific number. For example, using 10 as a base, the number 2583.789 is actually (2 × 10³) + (5 × 10²) + (8 × 10¹) + (3 × 10⁰) + (7 × 10^-1) + (8 × 10^-2) + (9 × 10^-3).

How do you convert from the binary to decimal system—and vice versa?

Besides the decimal system, one of the most familiar number systems is the binary numeration system; this is mainly because of its use in computers (for more about computers, see “Math in Computing”). In a binary numeration system, only 1 and 0 are used, or a base 2 system. Converting between binary and decimal systems is fairly simple; just remember that each digit in the binary number represents a power of two.

The first column in the base two math is the units column, then the twos, fours, eights, etc. columns, all of which can only be filled with 0s or 1s. Since there is no single digit that stands for “2” in base 2, when you get to what stands for 2, you put a 1 in the 2’s column and a 0 in the units column, creating one 2 and no 1s. Thus, the base ten “two” (2₁₀ or just 2 in decimal form) is written in the binary as 10₂; a 3 (3₁₀, or just 3 in decimal form) in base 2 is actually “one 2 and one 1,” or 11₂. The number 4 is actually 2 × 2, so you eliminate the 2’s and unit columns and put a 1 in the 4s column. Thus, 4₁₀ (or just 4 in decimal form) is written in binary form as 100₂. To see how computers “translate” decimal to binary numbers, here are the first ten conversions:

How do you express certain numbers in powers of ten notation?

A number in power of ten notation is represented as a base number (or mantissa) times ten raised to some power (or exponent). This means the mantissa is multiplied by ten times the number of times the power indicates. For example, in the equation 32 × 104, the 32 is the mantissa multiplied by 10 × 10 × 10 × 10. This would equal 320,000.

Power of ten notation can also be used to express the same number in various ways. For example, the distance from the Earth to the Sun averages 93,000,000 miles. This can be represented by the following:

93,000,000

93 × 106

9.3 × 107

or 0.93 × 108, and so on.

Why do mathematicians and scientists often use scientific notation?

Scientific notation is a way of making larger and smaller numbers used in the scientific field easier to write, read, and take up less space in calculations. Scientists generally pick the power of ten that is multiplied by a number between 1 and 10 to express these numbers. For example, it is easier to write 0.00023334522 as 2.3334522 × 10–4. To apply this to a scientific example, take the case of the average distance between the Earth and Sun, written in scientific notation as 9.3 × 107 miles—mathematically much easier to work with than the larger number it represents.

The following are several examples of large and small numbers in powers of ten notation similar to numbers used in scientific notation (note: numbers that are extremely small in scientific notation will have negative exponents):

748,000 can be represented by 7.48 × 105

245 can be represented by 2.45 × 102

-45,000 can be represented by -4.5 × 10⁴

0.025 can be represented by 2.5 × 10^-2

-0.0036 can be represented by -3.6 × 10^-3

0.0000409 can be represented by 4.09 × 10^-5

0.0000000014 can be represented by 1.4 × 10^-9

The average distance between the Earth and the Sun is most easily expressed using powers of ten as 9.3 × 10⁷.

What prefixes define the powers of ten?

Many standard prefixes are used to represent powers of ten, most of which are employed quite frequently to express various units. We are all familiar with some of them, including kilo- (from the Greek chilioi, or “a thousand”), milli- (from the Latin mille, or “thousand”), and micro- (from the Greek mikros, or “small”). The following chart defines some prefixes representing the powers of ten:

THE CONCEPT OF ZERO

What is a placeholder?

A placeholder is a number that, as the name implies, holds a place. Initially, various cultures used a placeholder—often a dot or a space—to show an empty spot or place not used in a numeral (or other way of counting). This was in place of what we now call a zero (0), a symbol that is not only a placeholder, but an essential number in our numeration system. (For more about the evolution of the symbol zero [0], see “History of Mathematics.”)

What are the definitions of zero and non-zero?

Those who use the Hindu-Arabic numeration system are all familiar with the concept of “zero” (0) and its importance. The symbol “zero” represents a valuable placeholder; it is also the additive identity element of an algebraic system (when a number and its additive inverse add up to 0); and finally, it is the starting point in measurements. The zero symbol is also called a cipher (no relation to sending secret messages) or the symbol for the absence of quantity, although be aware that cipher can also mean any Hindu-Arabic numeral. (Interestingly enough, the name “zero” is derived from the Arabic sifr, which means “cipher.”) In other words, zero is naught (nothing, or from the Old English, nāwiht, meaning “not” [na] and “thing” [wiht]).

Mathematicians also use the word non-zero to represent a quantity that does not equal zero. A real non-zero number must either be positive or negative; a complex non-zero number can be the real or imaginary part of the equation. (For more information about complex numbers, see above.)

What is an indeterminate number?

Like many other fields, mathematics has terms that sometimes confuse or overlap. For example, it is interesting to note that there is such a number as 0/0, which is called an indeterminate number. But be careful: This is not the same as an undefined number. If an indeterminate number comes up somewhere, you never know the value for your specific case—and you can conceivably give it any number of values. Confusing? Don’t worry, you’re not alone. It is one of those quandaries that often baffles the best mathematicians.

BASIC MATHEMATICAL OPERATIONS

What does an equal sign represent?

In standard arithmetic terms, the equal sign ( = ) is a symbol that represents two amounts with the same value. For example 7 = 7; or 3 + 4 = 7. When something is not equal, the sign is ≠, as in 2 ≠ 3 or 3 + 7 ≠ 12.

In a line of computer code, the equal sign can mean something much different. For example, for codes used under certain conditions, such as a JavaScript-reading computer, a single equal sign in a line of script means “is.” There is even a double equal sign (==) that means “is equal to,” an important difference when writing code for the computer. In addition—and confusing as it may seem—the computer codes for “not equal” are different, and include ! = and / =.

What is addition?

Addition is an operation in which two numbers, called the addends, produce a third number called the sum. Natural numbers are added by starting with the first addend and counting as many more numbers as the second addend. For example, for 2 + 4, you would think 2, 3 (as the first number after 2), 4 (as the second number), 5 (as the third number), and 6 (as the fourth number), thus the numbers add up to 6. Not all numbers are added in the same way as natural numbers.

What does carry mean in addition?

In addition, carry defines a way in which larger numbers are added. In this arithmetic operation, there is a shifting of leading digits into the next column to the left when the sum of that column exceeds a single digit. For example, carrying is evident in the following operation in the base 10 numbering system (adding addends 234 and 168 giving the sum 402):

When was the equal sign introduced into mathematics?

The equal sign (=) is a relatively “new” invention in mathematics. It was first used by British mathematician Robert Recorde (1510-1558; also seen erroneously as Record), in his book The Whetstone of Witte (1557), the first algebra book introduced in England. In it, he justifies using two parallel line segments “…bicause noe 2 thynges can be moare equalle (sic)…” (“because no two things can be more equal than parallel lines”). It was not an immediately popular symbol, though, with mathematicians continuing to use a range of symbols for equal, including two vertical parallel lines ( II ) used by Wilhelm Xylander in 1575, and ae or oe (both from the word aequalis, the Latin for “equal”). But for the most part, the word “equal” was written in an equation until around 1600, when Recorde’s symbol became more readily accepted, and it continues to be so today.

By adding the same columns, starting in the right hand column, 8 + 4 is 12, a number larger than 9, the highest number than can exist in that spot; carry the amount of ten to the next column, leaving 2; add 3 + 6 + 1 (which carried, represents 10 for this column), which equals 10, again a number larger than 9. Again, carry the one to the next column leaving 0; add the 2 + 1 + 1 (carried) equals 4. All total, the sum is 402.

How do you subtract numbers?

Subtraction is the “opposite” (or in set theory, the inverse) of addition: In its simplest form, one whole number is essentially taken away from another whole number. When you subtract numbers, you are answering the question of how many are left. For example, if 23 people leave a building that has 123 people (123 - 23), there would be 100 people left in the building.

What does borrow mean in subtraction?

Like “carry” in addition, to “borrow” in subtraction means to take amounts from one number and assign them to the next. In this procedure, the 10 is borrowed from the next higher digit column in order to obtain a positive difference in the nearby column. For example, borrowing is evident in the following operation in the base 10 numbering system (1,234 minus 567, giving the result of 667):

When you subtract the same columns, starting in the right hand column, the 4 is too small to subtract from 7; therefore, you need to borrow 10 from the column to the left, boosting the number 4 to 14. The column to the left then loses ten, and 2 is left. Again, the 2 is too small to subtract from 6, so 10 is borrowed from the next column to the left, boosting the number 2 to 12. The last number to the left is dropped down by 10, giving 11; the 5 is subtracted from the 11, resulting in 6 in that column.

Where did the symbols plus (+) and minus (-) originate?

One of the first books to use the plus and minus signs was written in 1489, Johann Widmann’s (c. 1460-?) Mercantile Arithmetic. Originally, he used the signs + and - to indicate excesses and deficits (what we would call credit and debit) in business dealings. But some historians believe the + sign initially evolved from the French et, or “and,” because the “e” and “t” resemble the + sign.

Although they were probably used before in general mathematics, the first person known to have used the + and - symbols in writing algebraic expressions lived in the early 1500s: the Dutch mathematician Vander Hoecke. The symbols finally went into general use in England when Robert Recorde’s (1510-1558; also seen erroneously as Record) book The Whetstone of Witte was published; this is the same book responsible for bringing the equal (=) sign to the forefront of mathematics (see above).

What is multiplication?

Multiply comes from the Latin roots multi (“many”) and pli (“folds”). English poet Geoffrey Chaucer (c. 1340-1400) may have used the word first as a verb in his A Treatise on the Astrolab (1391). In multiplication, two natural numbers are multiplied together (the numbers are called factors; the less used terms for two such numbers are multiplicand and multiplier) producing what is called a product. Multiplication is actually a form of repeated addition. For example, 2 × 3 means 2 + 2 + 2 (or 6).

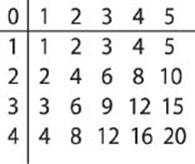
What are multiplication tables?

Multiplication tables are just as the name implies: a table of multiplication. Most of these tables have a specific purpose: mainly to multiply numbers in the rows and columns by each other to find a product.

English poet Geoffrey Chaucer may have used the word “multiplication” first as a verb in his A Treatise on the Astrolab (1391).

One of the simplest multiplication tables deal with the whole numbers. Here is one example:

Where did the symbols for multiplication originate?

The 17th century seems to have been the century when the basic mathematical symbols were developed. The best reasons for the development of such symbols make sense: they were faster and easier to write, took up less written space, and helped the printing process. Although the use of these symbols would eventually be standard—so everyone would understand the meaning of certain mathematical operations—it took a while for this to happen.

For example, in 1686, German mathematician Gottfried Wilhelm Leibniz (1646–1716) was using the symbol ∩ for multiplication and ∪ for division. Eventually, English mathematician and scientist Thomas Harriot (also seen as Hariot; 1560-1621) used the dot to indicate multiplication in his treatise Artis anayticae praxis, published posthumously in 1631. (He also developed the greater than [>] and less than [<] symbols). That same year, English mathematician William Oughtred (1575–1660) used the symbol “x” for multiplication in his book, Clavis mathematicae, in which he was also the first to mention the plus-minus symbol (±).

Today, we use a number of symbols for multiplication operations. The most common symbols are ×, *, ^., and ( ), as in 2 × 3, 2*3, 2 ^. 3, and (2)(3).

How is the term inverse used in arithmetic operations?

Inverse operations are those that “undo” another operation. In particular, subtraction is the inverse of addition because a + b - b = a; division is also the inverse operation to multiplication.

The inverse of a number can be expressed as follows: The additive inverse of a real or complex number a is the number that, when added to a, equals 0. In multiplication, the multiplicative inverse of a is the number that, when multiplied by a, equals 1.

What is division?

The word divide comes from the Latin root vidua (referring to a separation; the word “divide” shares its major root with the word “widow”) and di, a prefix that is a contrac tion of dis, meaning “apart” or “away.” In division, the number being divided is called the dividend, while the number dividing is called the divisor. The end result is called the quotient. For example, in 20/5 = 4, 20 is the dividend, 5 the divisor, and 4 the quotient.

Why can’t you divide by zero?

Dividing by zero is like the old saying, “You can’t get something from nothing.” Mathematically speaking, it’s the same way: You can’t “divide by nothing.” In fact, when something is divided by zero, the answer is always undefined.

Here are a few ways of looking at this: There is a rule in arithmetic that a(b/a) = b. So if we say that 1/0 = 5, then 0(1/0) = 0 × 5 = 0. In other words, if you could divide by 0, this rule would not work. Another way to look at the “no to 0 as a divisor” problem is through multiplication: if 10/2 = 5, we know that 5 × 2 = 10; the same for 5/1 = 5, thus we know that 5 × 1 = 5. But if you take 5/0, that would mean that the answer times 0 would equal 5, but anything times 0 is equal to zero. Because there is no answer to this dilemma, mathematicians say you can’t divide by zero.

Division in mathematics is a relatively new concept for the masses; it was only taught at university levels after the 16th century. The first to offer division to the public was German mathematician Adam Ries (1492-1559; also seen as Risz, Riesz, Riese, or Ris) in his work Rechenung nach der lenge, auff den Linihen vnd (sic) Feder, often shortened to Practica. His work reached more people for an important reason: Instead of the usual practice of writing a mathematical book in Latin, he wrote his book in German, thus reaching a wider audience.

Where did the symbols for division originate?

The history behind the division symbols is long and complicated. The following lists how the major ones developed:

Closed parentheses—The arrangement “8)24” was used by Michael Stifel (1486 or 1487-1567) in Arithmetica integra, published in 1544. It eventually evolved into the closed parentheses, such as (8)(4).

The obelus—By 1659, Swiss mathematician Johann Heinrich Rahn (1622–1676) introduced the division symbol (÷, called an obelus) in his book Teutsche Algebra, a combination of “:” and “-”. (This division symbol was used by many writers before Rahn as a minus sign.) In 1668, when Rahn’s book was translated into English, with additions by English mathematician John Pell (1610–1685), the division symbol was retained. Some say Pell greatly influenced Rahn to develop the symbol, but most historians agree that there is little evidence of such a connection.

Slash—Another sign for division (/), the slash is actually first used for fractions, such as 2/3 or ½. It can be extended into other, larger or smaller numbers, such as 123/112 and 0.112/0.334. Little is known about its origins, but it is known that this symbol was sometimes used for subtraction, until it became standard practice for representing division.

How did the symbols for long division develop?

In the 19th century, U.S. textbooks typically showed long division with the divisor, dividend, and quotient on the same line, separated by parentheses, as 36)108(3. In the same century, in examples of short division, a vinculum (line) was placed under the dividend, with the vinculum almost attached to the bottom of the parenthesis. The quotient was written under the vinculum, as per the following:

By late in the 19th century, the vinculum is almost attached to the top of the parenthesis and the quotient is written above the vinculum, as per the following:

These symbols are similar to what we see in our elementary dealings with long division, but our vinculum is attached to the parenthesis. Interestingly enough, there is no name for the symbol used for long division ( )^—-).

What is the least common multiple and denominator?

The smallest common multiple (whole number) of two or more whole numbers is called the lowest (or least) common multiple (LCM). For example, for the numbers 3 and 8, the multiples of 8 are 8, 16, 24, 32, and so on; the multiples of 3 are 3, 6, 9, 12, 15, 18, 21, 24, 27, and so on. Therefore, the LCM of 3 and 8 is 24.

The least common denominator (or LCD) is mainly used to carry out the addition or subtraction of fractions. In order to do these operations, the fractions need to have the same denominator. (For more information about fractions, see below.) The easiest way to work on such calculations is to determine the lowest number possible for the denominator—a number called the least common denominator (LCD)—which is actually the common factor by which two numbers are divisible. For example, to add 1/6 and 1/8, we have to find the least common multiple of the denominators. In this case, the number is 24: Multiply 1/6 × 4/4 and 1/8 × 3/3, to change each addend to some number of “24ths”; or 1/6 × 4/4 = 4/24; and 1/8 × 3/3 = 3/24. Thus, 1/6 + 1/8 = 4/24 + 3/24 = (4+3)/24 = 7/24.

What is the root of a number?

The root of a real or complex number is a number that, when raised to some exponent (or multiplied by itself the number of times indicated by the exponent), equals the original number. Most people are familiar with square and cube roots. There are actually many other such roots, including the real fourth roots, real fifth roots, and so on, and roots associated with complex numbers. For example, the real fourth roots of 16 are 2 and -2; the real fifth root of -32 is -2.

What are square and square roots?

When you multiply a real or complex number by itself, you are actually squaring that number. Mathematicians express the square of a number using the superscript 2, or, for example, 2². The square of a real number is always positive, whether the number is 2² (= 4) or -2² (= 4; a negative times a negative equals a positive real number).

A square root is a number that when multiplied by itself equals a specific product. For example, if t² = s, then , in which t is the square root and s is a positive number. For example, the two square roots of are 4 and -4, as 4² = 16 and -4² = 16.

What are a cube and cube root?

Much like a square, a cube is when you multiply a real or complex number by twice itself (making a total of three numbers). Mathematicians express the cube of a number using the superscript 3; or, for example, 2³, or 2 × 2 × 2. Unlike a square of a number, the cube of a number will not always be positive, such as -3 × -3 × -3, which equals -9.

A cube root is a number that when multiplied by itself two more times has the product of s, in which t³ = s. For example, the cube root of 125 (s) is 5 (t), or written as ; the cube root of -125 is -5.

What does a factor and factorization mean?

A factor is a portion of a quantity that when multiplied by other factors gives the entire quantity (or product). In order to determine such factors (or divisors), you have to use factorization (also called factoring or to factor). When factoring an integer, it is referred to as prime factorization; when factoring a polynomial, it is called polynomial factorization.

What is prime factorization?

Many of us are most familiar with prime factorization, which is a way of taking a number and breaking it down into its constituent primes. An example of prime factorization is as follows: One finds the “simplest” representation of the given quantity in terms of smaller parts—in the case of 15, the factors would be 1, 3, 5, and 15 (essentially, all the numbers that will divide integrally into 15). Not that prime factorization is always that easy. Larger numbers make it more difficult to factor, and many sophisticated prime algorithms have been devised for larger—and different types—of numbers.

What does the greatest common factor mean?

The greatest common factor (or GCF; sometimes called highest common factor) of two whole numbers is the largest whole number that is a factor of both. Take, for example, the numbers 12 and 15: The factors of 12 are 1, 2, 3, 4, 6, and 12; the factors of 15 are 1, 3, 5, and 15. Therefore, the common factors—or numbers in both lists of factors—are 1 and 3; therefore, the greatest (highest) common factor is 3.

There is another method used to discover the GCF: listing the numbers’ prime factors, then multiplying those numbers. For example, the prime factorization of 12 and 15 are: 2 × 2 × 3 = 12 and 3 × 5 = 15. Notice that the prime numbers have 3 in common; thus, the GCF is 3.

An example with larger numbers is to find the GCF of 36 and 54. Working it out by the first method, the factors of 36 are 1, 2, 3, 4, 6, 9, 12, 18, and 36; the factors of 54 are 1, 2, 3, 6, 9, 18, 27, and 54. The greatest (or highest) common factor of both numbers is 18. To work it out using prime factorization, the prime factorization of 36 is 2 × 2 × 3 × 3; the prime factorization of 54 is 2 × 3 × 3 × 3. Both these factorizations have one 2 and two 3s in common; thus, we multiply those common numbers, or 2 × 3 × 3 = 18.

FRACTIONS

What are proper and improper fractions?

The word “fraction” to most of us means a part of something; in mathematics, it represents a type of numeral, in most cases the quotient of two integers, with the top number called the numerator (the number of parts) and the bottom number the denominator (how many parts the whole is divided into). Written, the numerator and denominator are separated by a “/” or “—”. A fraction is usually denoted by a/b, in which “a” and “b” are whole numbers and “b” is not equal to zero (for the explanation of why you cannot divide by zero, see above).

Proper fractions are used to express parts of a whole. For example, in this photo there are four apples but only one red apple. One in four, or 1/4, of the apples is a red apple. In an improper fraction, the numerator is larger than the denominator, such as 4/3 or 3/2.

A rational number between 0 and 1 can be represented by fractions (by the division of two numbers). If the quotient is less than one, such as ½ or 2/5, then it is called a proper fraction; if the quotient is greater than one—or in other words, if the numerator of a fraction is larger than the denominator, such as 23/7—it is called an improper fraction.

How are fractions converted to decimals and vice-versa?

In the most commonly used place value, the decimal system, numbers smaller than 1 can be expressed as fractions, called decimal fractions. In this system, the decimal fractions are expressed in terms of tenths, hundredths, thousandths, and so on. For example, for the fraction ½, or 1 divided by 2, the decimal fraction is 0.5; and vice versa, the decimal fraction 0.5, or 5/10ths, is equal to ½.

Not all fractions are so easily converted to decimals. It depends on the type of number, especially if it is an irrational or rational number. Some decimal fractions include an infinite number of decimal places to be expressed exactly; something that is not possible as far as we know (who can write an infinite number of numbers?). And some decimal fractions repeat forever, such as 1/3 _ 0.3333.…

What are the rules for adding and subtracting fractions?

When adding fractions, the denominators need to be the same, but you can’t add the denominators to get the answer. Simply put, if the denominators are already the same, the fractions are simple to add, such as 1/3 + 1/3 = (1 + 1)/3 = 2/3. If the denominators are not the same, find the common denominator by multiplication. For example, 1/2 + 1/3 + 3/6 + 2/6 = (3 + 2)/6 = 5/6.

Can a fraction’s numerator be zero?

In the text on division (see above), we learned that it is not possible to divide by 0, which is labeled an undefined number. But you can have zero (0) as your numerator. And any allowed fraction (one that doesn’t have a 0 in the denominator) that has 0 as its numerator will always be equal to zero (0). For example, 0/5 and 0/345 both equal 0.

When subtracting fractions, the denominators again need to be the same; and you can’t add (or subtract) the denominators to get the answer. If the denominators are the same, subtract the fractions, such as 2/3 - 1/3 = (2 - 1)/3 = 1/3. If the denominators are not the same, find the common denominator by multiplication, such as ½ -1/3 = 3/6 - 2/6 = (3 - 2)/6 = 1/6.

What are the rules for multiplying and dividing fractions?

As to be expected, there are rules for multiplying and dividing fractions. Multiplication of factions is very straight forward—just multiply the numerators and denominators, then simplify the resulting fraction, if needed (or if you can). For example, 2/5 × 4/7 = (2 × 4) / (5 × 7) = 8/35 (this number cannot be simplified).

Division of fractions entails one main rule: You need to flip over, or invert, the “divisor” fraction (the fraction on the bottom) to get the result (this is also called the reciprocal of the fraction; see below). Here are the steps: First change the division sign to a multiplication sign after inverting the fraction to the right of the sign. Multiply the numerators and denominators and write the result. You can then simplify or reduce the fraction if needed. For example, ½ ÷ 1/4 = ½ × 4/1 = 4/2. This number can be simplified to 2.

How are decimal fractions added, subtracted, multiplied, and divided?

Decimal fractions are added, subtracted, multiplied and divided much like whole numbers—but with decimal differences. The following gives some examples: Adding such numbers as 0.3 + 0.2 is simple: 0.3 + 0.2 = 0.5. Adding whole and decimal fractions is also easy: 2.4 + 5 = 7.4. These numbers are also easy to subtract, such as 0.3 – 0.2 = 0.1. Multiplication and division are also similar to regular numbers, although the placement of the decimal point is ever-important. For example, multiplying 24.45 × 0.002 = 0.0489; dividing the same numbers 24.45/.002 = 12,225. (It’s interesting to note here a “mathematical surprise”: In the last example, dividing the small numbers equaled a much larger number—the opposite of what most of us would expect.)

What are unit fractions and how are they tied to ancient Egypt?

Aunit fraction is one that has a numerator of 1, such as ½, 1/4, and 1/43545. One of the earliest discussions of unit fractions—a table of representations of 1/n—was found on the famous Rhind papyrus (also called the Rhind Mathematical Papyrus), dated to around 1650 B.C.E. This record—a table copied by the Egyptians from another papyrus dated 200 years earlier—represented a sum of distinct unit fractions for odd “n” numbers between 5 and 101. To write a certain fraction, they would add combinations of 1/n. For example, instead of writing 2/5, they wrote 1/3 + 1/15; for 2/29, they wrote 1/24 + 1/58 + 1/174 + 1/232.

Because of the Rhind papyrus discovery, the sums of unit fractions are now called Egyptian fractions. No one truly knows why the Egyptians chose this method for representing fractions, but some historians believe it was a “wrong turn” in Egyptian mathematical history. Whatever the reason, the Egyptians (apparently successfully) used this system for 2,000 years. (For more information about the Rhind papyrus, see “History of Mathematics.”)

How do you reduce a fraction?

To reduce a fraction, there are three general steps: factor the numerator, factor the denominator, and cancel out the fractional mixes that have the value of one. The leftover number is the reduced fraction. For example, to reduce 16/56, factor the numerator (16 = 2 × 2 × 2 × 2) and factor the denominator (56 = 2 × 2 × 2 × 7); eliminate the 2s (2/2 equals 1):

How do you find an equivalent fraction?

An equivalent fraction—also called a “building fraction”—is the reverse of reducing the fraction: Instead of searching for the 1 in the fractional mix that you can reduce, you insert a 1 and build the fractions. For example, find the equivalent fraction for 1/4, using the number 3, multiply the numerator and denominator by 3 (3/3 = 1); 1/4 × 3/3 = 1 × 3/ 4 × 3 = 3/12; therefore the equivalent fraction in this case is 1/4 = 3/12 (the equal sign is used to represent equivalent fractions).

What is the reciprocal of a number?

The reciprocal of a number is obtained when a given number is divided into 1: the results are called the reciprocal of that number. For example, the reciprocal of 6 is 1 divided by 6, or 1/6. Reciprocals come in most handy when dividing fractions (see above to learn more about dividing fractions).