The history of mathematics: A brief course (2013)

Part II. The Middle East, 2000–1500 BCE

Chapter 7. Algebra and Geometry in Ancient Egypt

Although arithmetic and geometry fill up most of the Egyptian papyri, there are some problems in them that can be considered algebra, provided that we use the very general definition introduced in Chapter 1—that is, the study of techniques for giving the explicit value of a number starting from conditions that determine it implicitly. Most of these problems involve direct proportion and thus lead to linear (first-degree) equations. In the present chapter, we shall examine a selection of these problems and then look at some that have geometric application. In both areas, the goal is to get numerical answers using the computational techniques described in the preceding chapter.

7.1 Algebra Problems in the Rhind Papyrus

The concept of proportion is the key to the problems based on the “rule of false position.” Problem 24 of the Rhind papyrus, for example, asks for the quantity that yields 19 when its seventh part is added to it. The author notes that if the quantity were 7 (the “false [sup]position”), it would yield 8 when its seventh part is added to it. Therefore, the correct quantity will be obtained by performing the same operations on the number 7 that yield 19 when performed on the number 8. Thus, we first “calculate with 8 until we reach 19”:

Next, perform these same operations on 7:

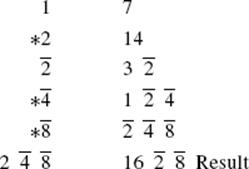
This is the answer. The scribe seems quite confident of the answer and does not carry out the computation needed to verify that it works. Notice that it involves the Horus-eye fractions. These fractions were obviously the easiest to work with, and so occur very frequently in the problems we shall be considering.

The Egyptian scribes were capable of performing operations more complicated than mere proportion. They could take the square root of a number, which they called a corner. The Berlin papyrus 6619, contains the following problem (Gillings, 1972, p. 161):

The area of a square of 100 is equal to that of two smaller squares. The side of one is the side of the other. Let me know the sides of the two unknown squares.

Here we are asking for two quantities given their ratio () and the sum of their squares (100). The scribe assumes that one of the squares has side 1 and the other has side . Since the resulting total area is 1 , the square root of this quantity is taken (1 ), yielding the side of a square equal to the sum of these two given squares. This side is then multiplied by the correct proportionality factor so as to yield 10 (the square root of 100). That is, the number 10 is divided by 1 , giving 8 as the side of the larger square and hence 6 as the side of the smaller square. This example, incidentally, was cited by van der Waerden as evidence of early knowledge of the Pythagorean theorem in Egypt.

7.1.1 Applied Problems: The Pesu

The Rhind papyrus contains problems that involve the concept of proportion in the guise of the slope of pyramids and the strength of beer. Both of these concepts involve what we think of as a ratio, along with the technique of finding the fourth element in a proportion by the procedure once commonly taught to grade-school students and known as the Rule of Three. (See Section 2.3 of Chapter 2.) Since the Egyptian procedure for multiplication was based on an implicit notion of proportion, such problems yield easily to the Egyptian techniques, as we shall see below. Several units of weight are mentioned in these problems, but the measurement we shall pay particular attention to is a measure of the dilution of bread or beer. It is called a pesu and defined as the number of loaves of bread or jugs of beer obtained from one hekat of grain. A hekat was slightly larger than a gallon, 4.8 liters to be precise. Just how much beer or bread it would produce under various circumstances is a technical matter that need not concern us. The thing we need to remember is that the number of loaves of bread or jugs of beer produced by a given amount of grain equals the pesu times the number of hekats of grain. A large pesu indicates weak beer or bread. In the problems in the Rhind papyrus the pesu of beer varies from 1 to 4, while that for bread varies from 5 to 45.

Problem 71 tells of a jug of beer produced from half a hekat of grain (thus its pesu was 2). One-fourth of the beer is poured off, and the jug is topped up with water. The problem asks for the new pesu. The author reasons that the eighth part of a hekat of grain was removed, leaving (in his terms) , that is, what we would call of a hekat of grain. Since this amount of grain goes into one jug, it follows that the pesu of that beer is what we call the reciprocalof that number, namely 2 . The author gives this result immediately, apparently assuming that by now the reader will know how to “calculate with until 1 is reached.”

The Rule of Three procedure is invoked in Problem 73, which asks how many loaves of 15-pesu bread are required to provide the same amount of grain as 100 loaves of 10-pesu bread. The answer is found by dividing 100 by 10, then multiplying by 15, which is precisely the Rule of Three.

7.2 Geometry

The most fascinating aspect of Egyptian mathematics is the application of these computational techniques to geometry. In Section 109 of Book 2 of his History, the Greek historian Herodotus writes that King Sesostris¹ dug a multitude of canals to carry water to the arid parts of Egypt. He goes on to connect this Egyptian engineering with Greek geometry:

It was also said that this king distributed the land to all the Egyptians, giving an equal quadrilateral farm to each, and that he got his revenue from this, establishing a tax to be paid for it. If the river carried off part of someone's farm, that person would come and let him know what had happened. He would send surveyors to remeasure and determine the amount by which the land had decreased, so that the person would pay less tax in proportion to the loss. It seems likely to me that it was from this source that geometry was found to have come into Greece. For the Greeks learned of the sundial and the twelve parts of the day from the Babylonians.

The main work of Egyptian surveyors was measuring fields. That job is literally described by its Latin name agrimensor. Our word surveyor comes through French, but has its origin in the Latin supervideo, meaning I oversee. The equivalent word in Greek was used by Herodotus in the passage above. He described episkepsoménous kaì anametrsontas , using future participles that mean literally “[people who] will be inspecting for themselves and measuring carefully.”² The process of measuring a field is shown in a painting from the tomb of an Egyptian noble named Menna at Sheikh Abd el-Qurna in Thebes. Menna bore the title Scribe of the Fields of the Lord of the Two Lands during the Eighteenth Dynasty, probably in the reign of Amenhotep III or Thutmose IV, around 1400 BCE. His job was probably that of a steward, to oversee planting and harvest. The instrument used to measure distance was a rope that could be pulled taut. That measuring instrument has given rise to another name often used to refer to these surveyors: harpedonáptai, from the words harpedón, meaning rope, and hápt, meaning I attach. The philosopher Democritus (d. 357 BCE) boasted, “In demonstration no one ever surpassed me, not even those of the Egyptians called harpedonáptai.”³

The geometric problems considered in the Egyptian papyri all involve numerical measurement rather than the more abstract proportions that make up the bulk of Greek geometry. These problems show considerable insight into the properties of simple geometric figures such as the circle, the triangle, the rectangle, and the pyramid; and they rise to a rather high level of sophistication in computing the area of a hemisphere. The procedures for measuring regions with flat boundaries (polygons and pyramids) are correct from the point of view of Euclidean geometry, while those involving curved boundaries (disks and spheres) have an error controlled entirely by the error in the ratio the area of a circle bears to the square on its diameter. In the papyrus, this ratio is given as . In Euclidean geometry, it is .

7.3 Areas

Since the areas of rectangles and triangles are easy to compute, it is understandable that very little attention is given to these problems. Only four problems in the Rhind papyrus touch on these questions, namely Problems 6, 49, 51, and 52.

7.3.1 Rectangles, Triangles, and Trapezoids

Problem 49 involves computing the area of a rectangle that has dimensions 1 khet by 10 khets. This in itself would be a trivial problem, except that areas are to be expressed in square cubits rather than square khets. Since a khet is 100 cubits, the answer is given correctly as 100,000 square cubits. Problem 51 is a matter of finding the area of a triangle, and it is illustrated by a figure showing the triangle. The area is found by multiplying half of the base by the height. In Problem 52, this technique is generalized to a trapezoid, and half of the sum of the upper and lower bases is multiplied by the height.

Of all these problems, the most interesting is Problem 6, which involves a twist that makes it equivalent to a quadratic equation. A rectangle is given having area 12 cubit strips; that is, it is equal to an area 1 cubit by 12 cubits, though not of the same shape. The problem is to find its dimensions given that the width is three-fourths of the length ( in the notation of the papyrus). The first problem is to “calculate with , until 1 is reached,” that is, in our language, dividing 1 by . The result is . Then 12 is multiplied by , yielding 16, after which the scribe takes the corner (square root) of 16, getting 4 as the length. This is a very nice example of thinking in terms of descriptions that determine a quantity and using those descriptions to exhibit its value explicitly, exactly what we are defining algebra to be. The scribe seems to have in mind a picture of the length being multiplied by three-fourths of the length, the result being 12. This 12, which is of the square of the length, is multiplied by the reciprocal of , after which the length is found by taking the square root. From the scribe's point of view, the heart of the problem was getting the reciprocal of .

7.3.2 Slopes

Given that the Egyptians had no trigonometry as we now understand it, it is interesting to observe the solutions of problems that involve the slope of the sides of pyramids and other figures. There is a unit of slope analogous to the pesu that we have just seen in the problems involving strength of bread and beer. The unit of slope is the seked, defined as the number of palms of horizontal displacement associated with a vertical displacement of 1 royal cubit. One royal cubit was 7 palms. Because of the relative sizes of horizontal and vertical displacements, it makes sense to use the larger unit of length (the cubit) for vertical distances and the smaller one (the palm) for horizontal distances, even at the expense of introducing an extra factor into computations of slope. In our terms the seked is seven times the tangent of the angle that the sloping side makes with the vertical. In some of the problems the seked is given in such a way that the factor of 7 drops out. Notice that if you were ordering a stone from the quarry, the seked would tell the stonecutter immediately where to cut. One would mark a point one cubit (distance from fingertip to elbow) from the corner in one direction and a point at a number of palms equal to the seked in the perpendicular direction and then simply cut between the two points marked.

In Problem 57 a pyramid with a seked of 5 and a base of 140 cubits is given. The problem is to find its height. The seked given here ( of 7) is exactly that of one of the actual pyramids, the pyramid of Khafre, who reigned from 2558 to 2532 BCE. It appears that stones were mass-produced in several standard shapes with a seked that could be increased in intervals of one-fourth. Pyramid builders and designers could thereby refer to a standard brick shape, just as architects and contractors since the time of ancient Rome have been able to specify a standard diameter for a water pipe. Problem 58 gives the dimensions of the same pyramid and asks for its seked, apparently just to reinforce the reader's grasp of the relation between seked and dimension.

7.3.3 Circles

Five of the problems in the Rhind papyrus (41–43, 48, and 50) involve calculating the area of a circle. The answers given are approximations, but, as mentioned above, would be precise if the value 64/81 used in the papyrus where we would use π/4 were exact. The author makes no comment suggesting that this value is only an approximation. Nor should we expect him to, since he would have had no concept of infinite precision in measuring continuous objects.

A Digression: Commercial Computation of Volumes. When physical objects such as grain silos are built, the parts used to build them have to be measured. In addition, the structures and their contents have a commercial, monetary value. Some number has to be used to express that value. It would therefore not be absurd—although it would probably be unnecessary—for a legislature to pass a bill prescribing a numerical value to be used for π.⁴ Similarly, the claim often made that the “biblical” value of π is 3, based on the description of a vat 10 cubits from brim to brim girdled by a line of 30 cubits (1 Kings 7:23) is pure pedantry. It assumes more precision than is necessary in the context. The author may have been giving measurements only to the nearest 10 cubits, not an unreasonable thing to do in a literary description.⁵ We now return to the subject of circle measurements in Egypt.

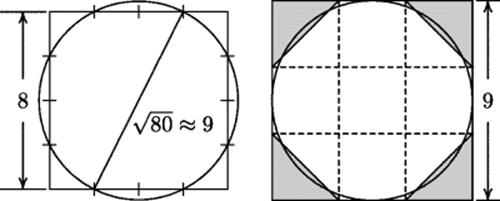
Ahmose takes the area of a circle to be the area of the square whose side is obtained by removing the ninth part of the diameter. In our language the area is the square on eight-ninths of the diameter; that is, it is the square on of the radius. In our language, not that of Egypt, this gives a value of π for area problems equal to . Please remember, however, that the Egyptians had no concept of the number π. The constant of proportionality that they always worked with represents what we would call π/4. There have been various conjectures as to how the Egyptians might have arrived at this result. One such conjecture, given by Robins and Shute (1987, p. 45), involves a square of side 8. If a circle is drawn through the points 2 units from each corner, it is visually clear that the four fillets at the corners, at which the square is outside the circle, are nearly the same size as the four segments of the circle outside the square; hence this circle and this square may be considered equal in area. Now the diameter of this circle can be obtained by connecting one of the points of intersection to the opposite point, as shown on the left-hand diagram in Fig. 7.3, and measurement will show that this line is very nearly 9 units in length (it is actually in length). A second theory due to K. Vogel [see Gillings (1972, pp. 143–144)] is based on the fact that the circle inscribed in a square of side nine is roughly equal to the unshaded region in the right-hand diagram in Fig. 7.1. This area is of 81, that is, 63. A square of equal size would therefore have side . In favor of Vogel's conjecture is the fact that a figure very similar to this diagram accompanies Problem 48 of the papyrus. A discussion of various conjectures, giving connections with traditional African crafts, was given by Gerdes (1985).

Figure 7.1 Conjectured explanations of the Egyptian squaring of the circle.

7.3.4 The Pythagorean Theorem

In the discussion of ancient cultures, the question of the role played by the Pythagorean theorem is of interest. Did the ancient Egyptians know this theorem? It has been reported in numerous textbooks, popular articles, and educational videos that the Egyptians laid out right angles by stretching a rope with 12 equal intervals knotted on it so as to form a 3–4–5 right triangle. What is the evidence for this assertion? First, the Egyptians did lay out very accurate right angles. Also, as mentioned above, it is known that their surveyors used ropes as measuring instruments and were referred to as rope-fixers. That is the evidence that was cited by the person who originally made the conjecture, the historian Moritz Cantor (1829–1920) in the first volume of his history of mathematics, published in 1880. The case can be made stronger, however. In his essay Isis and Osiris, the first-century polymath Plutarch says the following.

It has been imagined that the Egyptians regarded one triangle above all others, likening it to the nature of the universe. And in his Republic Plato seems to have used it in arranging marriages. This triangle has 3 on the vertical side, 4 on the base, and a hypotenuse of 5, equal in square to the other two sides. It is to be imagined then that it was constituted of the masculine on the vertical side, and the feminine on the base; also, Osiris as the progenitor, Isis as the receptacle, and Horus as the offspring. For 3 is the first odd number and is a perfect number;⁶ the 4 is a square formed from an even number of dyads; and the 5 is regarded as derived in one way from the father and another way from the mother, being made up of the triad and the dyad.

Finally, as mentioned above, Berlin papyrus 6619 contains a problem in which one square equals the sum of two others. It is hard to imagine anyone being interested in such conditions without knowing the Pythagorean theorem. Against the conjecture, we could note that the earliest Egyptian text that mentions a right triangle and finds the length of all its sides using the Pythagorean theorem dates from about 300 BCE, and by that time the presence of Greek mathematics in Alexandria was already established. None of the older papyri mention or use by implication the Pythagorean theorem.

On balance, one would guess that the Egyptians did know the Pythagorean theorem. However, there is no evidence that they used it to construct right angles, as Cantor conjectured. There are much simpler ways of doing that (even involving the stretching of ropes), which the Egyptians must have known. Given that the evidence for this conjecture is so meager, why is it so often reported as fact? Simply because it has been repeated frequently since it was originally made. We know precisely the source of the conjecture, but that knowledge does not seem to reach the many people who report it as fact.⁷

7.3.5 Spheres or Cylinders?

Problem 10 of the Moscow papyrus has been subject to various interpretations. It asks for the area of a curved surface that is either half of a cylinder or a hemisphere. In either case it is worth noting that the area is obtained by multiplying the length of a semicircle by another length in order to obtain the area. Finding the area of a hemisphere is an extremely difficult problem. Intuitive techniques that work on flat or ruled surfaces break down. If the Egyptians did compute this area, no one has given any reasonable conjecture as to how they did so. The difficulty of this problem was given as one reason for interpreting the figure as half of a cylinder. Yet the plain language of the problem implies that the surface is a hemisphere. The problem was translated into German by the Russian scholar V. V. Struve (1889–1965); the following is a translation from the German:

The way of calculating a basket, if you are given a basket with an opening of 4 . O, tell me its surface!

Calculate of 9, since the basket is half of an egg. The result is 1. Calculate what is left as 8. Calculate of 8. The result is . Calculate what is left of this 8 after this is taken away. The result is 7 . Calculate 4 times with 7 . The result is 32. Behold, this is the surface. You have found it correctly.

If we interpret the basket as being a hemisphere, the scribe has first doubled the diameter of the opening from to 9 “because the basket is half of an egg.” (If it had been the whole egg, the diameter would have been quadrupled.) The procedure used for finding the area here is equivalent to the formula . Taking as representing π/4, we find it equal to (πd²)/2, or 2πr², which is indeed the area of a hemisphere of radius r.

Van der Waerden points out (1963, pp. 33–34) that this value is also the lateral area of half of a cylinder of height d and base diameter d if it is laid on its side and bisected by a plane through the diameters of its two circular bases. In that case, the two bases are not counted as part of the area, and the basket must be regarded as a semicircular lamina attached to the two opposite sides of its top.⁸ In this case, the opening would be square, since its width is the height of the cylinder, its length is the diameter of the base, and the two are equal; the number would be the side of the square. That would mean also that the “Egyptian π” (π/4 = 64/81), used for area problems, which we refer to as two-dimensional π, was also being applied to the ratio of the circumference to the diameter, which we refer to as one-dimensional π. In other words, the Egyptians would have known that the ratio of the circumference to the diameter of a circle is the same as the ratio of the square on its radius to the disk it encloses. The numerical answer is consistent with this interpretation, but, as just mentioned, only the lateral surface of the cylinder is to be included. That would indicate that the basket was open at the sides. It would be strange to describe such a basket as “half of an egg.” The main reason given by van der Waerden for preferring this interpretation is an apparent inaccuracy in Struve's statement of the problem. Van der Waerden quotes T. E. Peet, who says that the number occurs twice in the statement of the problem, as the opening of the top of the basket and also as its depth. This interpretation, however, leads to further difficulties. If the surface is indeed half of a cylinder of base diameter , its depth is not ; it is . Van der Waerden also mentions a conjecture of Neugebauer, that this surface was intended to be a domelike structure of a sort seen in some Egyptian paintings, resembling very much the small end of an egg. That interpretation restores the idea that this problem was the computation of the area of a nonruled surface, and the approximation just happens to be the area of a hemisphere.

7.3.6 Volumes

One of the most remarkable achievements of the Egyptians is the discovery of accurate ways of computing volumes. In Problem 41 of the Rhind papyrus we find the correct procedure used for finding the volume of a cylindrical silo, that is, the area of the circular base is multiplied by the height. To make the numbers easy, the diameter of the base is given as 9 cubits, as in Problems 48 and 50, so that the area is 64 square cubits. The height is 10 cubits, giving a volume of 640 cubic cubits. However, the standard unit of grain volume was a khar, which is two-thirds of a cubic cubit, resulting in a volume of 960 khar. In a further twist, to get a smaller answer, the scribe divides this number by 20, getting 48 “hundreds of quadruple hekats.” (A khar was 20 quadruple hekats.) Problem 42 is the same problem, only with a base of diameter 10 cubits. Apparently, once the reader has the rule well in hand, it is time to test the limits by making the data more cumbersome. The answer is computed to be khar, again expressed in hundreds of quadruple hekats. Problems 44–46 calculate the volume of prisms on a rectangular base by the same procedure.

Given that pyramids are so common in Egypt, it is surprising that the Rhind papyrus does not discuss the volume of a pyramid. However, Problem 14 from the Moscow papyrus asks for the volume of the frustum of a square pyramid, given that the side of the lower base is 4, the side of the upper base is 2, and the height is 6. The author gives the correct procedure: Add the areas of the two bases to the area of the rectangle whose sides are the sides of the bases, that is, 2 · 2 + 4 · 4 + 2 · 4, then multiply by one-third of the height, getting 56. This technique could not have been arrived at through experience. Some geometric principle must be involved, since the writer knew that the sides of the bases, which are parallel lines, need to be multiplied. Normally, the lengths of two lines are multiplied only when they are perpendicular to each other, so that the product represents the area of a rectangle. Gillings (1972, pp. 190–193) suggests a possible route by which this knowledge may have been obtained. Robins and Shute (1987, pp. 48–49) suggest that the result may have been obtained by completing the frustum to a full pyramid and then subtracting the volume of the smaller pyramid from the larger. In either case, the power of visualization involved in seeing that the procedure will work is remarkable.

Like the surface area problem from the Moscow papyrus just discussed, this problem reflects a level of geometric insight that must have required some accumulation of observations built up over time. It is very easy to see that if a right pyramid with a square base is sliced in half by a plane through its vertex and a pair of diagonally opposite vertices of the base, the base is bisected along with the pyramid. Thus, a tetrahedron whose base is half of a square has volume exactly half that of the pyramid of the same height having the whole square as a base.

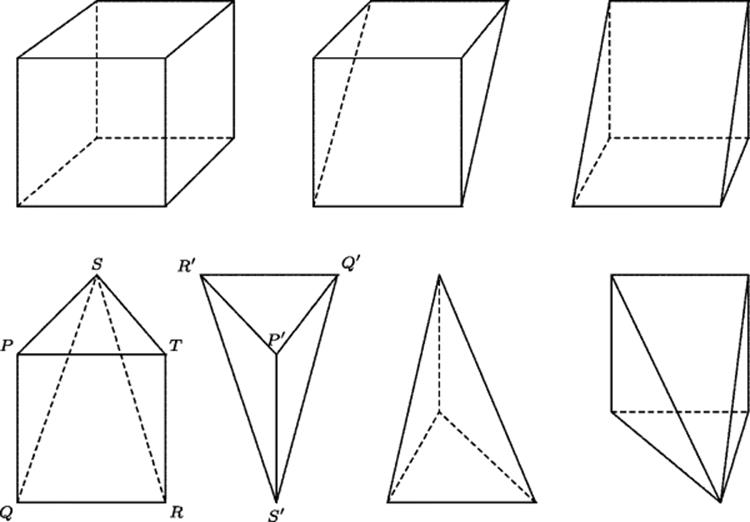
It is also easy to visualize how a cube can be cut into two wedges, as in the top row of Fig. 7.2. Each of these wedges can then be cut into a pyramid on a face of the cube plus an extra tetrahedron, as in the bottom row. The tetrahedron P' Q' R' S' has a base P' Q' R' that is half of the square base PQRT of the pyramid PQRST and hence has half of its volume. It follows that the volume of the tetrahedron is one-sixth that of the cube, and so the pyramid PQRST is one-third of the volume. A “mixed” geometric-mechanical strategy is also possible, involving weighing of the parts. The two tetrahedra would, in theory, balance one of the square pyramids. This model could be sawn out of stone or wood. From that special case one might generalize the vital clue that the volume of a pyramid is one-third the area of the base times the altitude.

Figure 7.2 Dissection of a cube into two square pyramids and two tetrahdra.

Once the principle is established that a pyramid equals a prism on the same base with one-third the height, it is not difficult to chop a frustum of a pyramid into the three pieces described in the Moscow papyrus. Referring to Fig. 7.3, which shows a frustum with bottom base a square of side a and upper base a square of side b with b < a, we can cut off the four corners and replace them by four rectangular solids with square base of side (a − b)/2 and height h/3. These four fit together to make a single solid with square base of side a − b and height h/3. One opposite pair of the four sloping faces that remain after the corners are removed can be cut off, turned upside down, and laid against the other two sloping faces so as to form a rectangular prism with a rectangular base that is a × b and has height h. The top one-third of this prism can then be cut off and laid aside. It has volume (h/3)ab. The top half of what remains can then be cut off, and a square prism of base side b and height h/3 can be cut off from it. If that square prism is laid aside (it has volume (h/3)b²), the remaining piece, which is (a − b) × b × (h/3), will fill out the other corner of the bottom layer, resulting in a square prism of volume (h/3)a². Thus, we obtain the three pieces that the scribe added to get the volume of the frustum in a way that is not terribly implausible.

Figure 7.3 Dissection of a frustum of a pyramid.

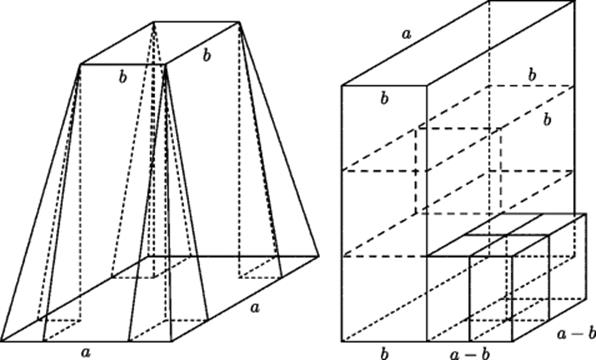
These last few paragraphs and Figs. 7.2 and 7.3 are conjectures, not facts of history. We do not know how the Egyptians discovered that the volume of a pyramid is one-third the volume of a prism of the same base and height or how they learned how to compute the volume of a frustum.

Problems and Questions

Mathematical Problems

7.1 Compare the pesu problems in the Rhind papyrus with the following problem, which might have been taken from almost any algebra book written in the past century: A radiator is filled with 16 quarts of a 10% alcohol solution. If it requires a 30% alcohol solution to protect the radiator from freezing, how much 95% solution must be added (after an equal amount of the 10% solution is drained off) to provide this protection? Think of the alcohol as the grain in beer and the liquid in the radiator as the beer. The liquid has a pesu of 10. What is the pesu that it needs to have, and what is the pesu of the liquid that is to be used to achieve this result?

7.2 Problem 33 of the Rhind papyrus asks for a quantity that yields 37 when increased by its two parts (two-thirds), its half, and its seventh part. Try to get the author's answer: The quantity is 16 . [Hint: The table for doubling fractions gives the last three terms of this expression as the double of . The scribe first tried the number 16 and found that the result of these operations applied to 16 fell short of 37 by the double of , which, as it happens, is exactly 1 times the double of .]

7.3 Find the height of the pyramid with a square base of side 140 cubits and seked equal to 5 (Problem 57 of the Rhind papyrus).

Historical Questions

7.4 Compare the procedures for computing volumes in ancient Mesopotamia with those used in ancient Egypt.

7.5 To what audience does the Rhind papyrus appear to be addressed?

7.6 What principles seem to determine the order of the problems discussed in the Rhind papyrus?

Questions for Reflection

7.7 Why not simply write to stand for what we call ? What is the reason for using two or three other “parts” instead of these two obvious parts?

7.8 We would naturally solve many of the problems in the Rhind papyrus using an equation. Would it be appropriate to say that the Egyptians solved equations, or that they did algebra?

7.9 What do you imagine was the social position of Ahmose, who wrote the Rhind papyrus? What were his normal duties, and for what purpose did he undertake this labor?

Notes

1. There were several pharaohs with this name. Some authorities believe that the one mentioned by Herodotus was actually Ramses II, who ruled from 1279 to 1212 BCE.

2. Or “remeasuring.”

3. Quoted by the second-century theologian Clement of Alexandria, in his Stromata (Miscellanies), Book 1, Chapter 15.

4. However, in the most notorious case where such a bill was nearly passed—House Bill 246 of the 1897 Indiana legislature—it was absurd. The bill was written by a physician and amateur mathematician named Edwin J. Goodwin. Goodwin had copyrighted what he thought was a quadrature of the circle. He offered to allow textbooks sold in Indiana to use his proof royalty-free provided that the Indiana House would pass this bill, whose text mostly glorified his own genius. Some of the mathematical statements the legislature was requested to enact were pure gibberish. For example, “a circular area is to the square on a line equal to the quadrant of the circumference, as the area of an equilateral rectangle is to the square on one side.” The one clear statement is that “the ratio of the chord and arc of ninety degrees. . .is as seven to eight.” That statement implies that . The square root in this expression did not trouble Dr. Goodwin, who declared that . At this point, one might have taken his value of π to be 160/49 = 3.265306122. . .. But, in a rare and uncalled-for manifestation of consistency, since he “knew” that 100/49 = (10/7)² = 2, Goodwin declared this fraction equal to 16/5 = 3.2. The bill was stopped at the last minute by lobbying from a member of the Indiana Academy of Sciences and was tabled without action.

5. However, like everything in the Bible, this passage has been subject to repeated analysis. For a summary of the conclusions reached in the Talmud, see Tsaban and Garber (1998).

6. The number 3 is not perfect according to the Euclidean definition, as Plutarch must have known. He uses the same words that Euclid uses for odd number (perissós, meaning a number having an excess (when divided by 2), and perfect number (téleios). Euclid defines a number to be perfect if it is equal to [the sum of] the numbers that measure it, that is, divide it evenly. If 1 is counted as a number that measures it and the number itself is not, then no prime can be perfect. If the opposite convention is adopted (since the Greeks generally didn't think of 1 as a number), then primes and perfect numbers are the same thing. What could Plutarch have been thinking?

7. This point was made very forcefully by van der Waerden (1963, p. 6). In a later book (1983), van der Waerden claimed that integer-sided right triangles, which seem to imply knowledge of the Pythagorean theorem, are ubiquitous in the oldest megalithic structures. Thus, he seems to imply that the Egyptians knew the theorem, but didn't use it as Cantor suggested.

8. If the cylinder is truncated by a plane parallel to its base and at height equal to half of the radius of the base, then one also gets the correct area. That is, the basket is an upright cylinder whose height is half the radius of its base.