Basic Math and Pre-Algebra

PART 1. The World of Numbers

CHAPTER 5. Fractions

Arithmetic with Fractions

When you work with fractions, the methods of whole number arithmetic are no longer enough to handle the job. You’ll need some new strategies for multiplying and adding. Once you have learned those methods, however, subtraction and division will just be variations and so not much more to learn. In fact, we’ll cover addition and subtraction together and multiplication and division together, because they have so much in common. Before that, however, you need to master the key to working happily with fractions: the art of disguise.

Equivalent Forms

The key to working successfully with fractions is to be able to find equivalent forms of the same fraction. All that means is that you can change the way a fraction looks without changing its worth. The simplest way to do that is to multiply by 1, in disguise.

Disguise? Well, the number 1 can be written as a fraction in many different ways: 4/4, 19/19, 73/73, or any number over itself. Multiplying a number by one will never change its value, but multiplying by 1 wearing the right disguise will change the number’s appearance.

You already know how to multiply by 1 when it appears as a whole number. In fact, you know that there is nothing to do when multiplying by 1, because multiplying a number by 1 doesn’t change it. But when the 1 puts on its fraction disguise, things are a little different. If, for example, you multiply 1/2 by 1, you know you should get a number equal to 1/2. But if the 1 is disguised as 5/5 the answer won’t look like 1/2, even though that’s what it will be worth.

There are lots of numbers that are worth 1/2. That fraction says the whole was divided into two parts, and you have one of them. If 2 wholes were each divided into two parts, there would be a total of 4 pieces. When the first whole is broken in 2, you should get 1 piece, and then when the second whole is broken, you should get 1 piece of that. You get 2 of the 4 pieces. 1/2 = 2/4. There are lots of other fractions that are equal to 1/2, and in fact, there are lots of names for any fraction. They all have the same value but different appearances.

You don’t want to break things into parts and count every time you need a fraction to change its appearance, so there’s a simple shortcut. For that shortcut, you need a little preview of fraction arithmetic. The basic rule for multiplying fractions says to multiply numerator times numerator and denominator times denominator. When you want to change the appearance of a fraction, multiply it by a disguised 1. 1/2 x 5/5 is still worth 1/2 because you’re multiplying by 1, but its appearance changes to 5/10. In the same way, 1/2 x 3/3 = 3/6 and 1/2 x 19/19 = 19/38. The same fraction can have many different looks.

You can go the other way, too, taking a fraction to a simpler appearance. This is officially called simplifying, but you’ll often hear it called reducing to lowest terms, or just reducing.

MATH TRAP

The expression “reducing a fraction” is a dangerous way to describe simplifying. It makes it sound like the fraction is getting smaller, but it's not. The appearance of the fraction is changing, but its value is not. If you must use “reduce”—and most people do—remember that the fraction hasn't changed. 3/5 may look smaller than 243/405, but it's the same number.

The fraction 16/36 can be written in a much simpler form. Find a number that divides both the numerator and denominator, preferably the GCF. In this case, that’s 4. Think of the fraction with the numerator and denominator factored:  Can you see the disguised 1 in there?  The fraction 4/9 is a simpler name for 16/36.

If you don’t know, or don’t want to look for, the GCF of the numerator and denominator, you can start the process with any number that divides both. Divide the numerator and denominator by the same number. Repeat until there are no other numbers that will divide both. It may take a while, but you’ll get there. If you start with the GCF, you’ll only need one try.

CHECK POINT

6. Change 1/5 to a fraction with a denominator of 40.

7. Change 3/4 to a fraction with a denominator of 28.

8. Change 5/7 to a fraction with a denominator of 147.

9. Simplify 35/40.

10. Simplify 63/84.

Multiplying and Dividing Fractions

Since you’ve already had a preview of the rule for multiplying fractions, let’s start the conversation about arithmetic there. The basic rule for multiplication of fractions calls for multiplying numerator times numerator and denominator times denominator, then simplifying if possible. To multiply 1/9 x 3/7, multiply 1 x 3 and 9 x 7. This gives you 3/63, which simplifies to 1/21, because 

Dividing fractions introduces only one extra piece to the multiplication rule. To divide fractions, invert the divisor and multiply. The divisor is always the second fraction. Invert only the divisor, never the first fraction. This inverted, or flipped, version of the fraction is called its reciprocal. To divide 1/8 ÷ 3/4, realize that the fraction 3/4 is the divisor. Invert 3/4 to get 4/3, then multiply and simplify: 

DEFINITION

Two numbers are reciprocals if when they are multiplied their product is 1. The reciprocal of the whole number 4 is the fraction 1/4. The reciprocal of a fraction is another fraction with the numerator and denominator switched. 3/8 and 8/3 are reciprocals. Each number is the reciprocal of the other.

Much of the work of multiplying and dividing fractions can be made easier by canceling before multiplying. Canceling is dividing a numerator and a denominator by the same common factor. You can think of it as simplifying before you multiply instead of after.

DEFINITION

Canceling is the process of simplifying a multiplication of fractions by dividing a numerator and a denominator by a common factor.

When you multiply 8/9 x 7/12 you multiply the numerators and multiply the denominators, so your product, before you actually get the multiplying done, is  After you do the multiplying, it’s 56/108, and that needs to be simplified. To simplify it, you’ll factor:  But look back to  for a moment. Can you see that you could factor this version? And because the numbers are smaller, it might be easier.  Both methods will leave you with 14/27. Canceling allows you to divide either numerator and either denominator by the same number. In that last example, it would look like this:

You need to multiply 8/9 x 7/12. You notice that both the numerator 8 and the denominator 12 have a factor of 4.

Divide each of them by 4, and show that by crossing out the original number and writing the quotient of that number and 4.

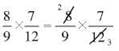
Multiply numerator times numerator and denominator times denominator, using the new numbers.

MATH TRAP

When cancelling, remember to divide a numerator and a denominator by the same number. Never divide two numerators or two denominators.

Let’s look at some examples. First, we’ll walk through 3/8 x 4/9.The basic rules says to multiply 3 times 4 and 8 times 9, giving the fraction 12/72, which reduces to 1/6. However, you can cancel before multiplying. Divide 3 into both 3 and 9, and divide 4 into both 4 and 8. The problem turns into 1/2 x 1/3.

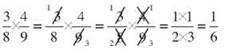
Let’s try one with a mixed number. That’s a whole number plus a fraction, but you can turn it into an improper fraction by finding the proper disguise for the whole number part.

Divide 

Whenever a multiplication or division problem involves a mixed number, convert to an improper fraction immediately. The 1 is equal to 14/14 and the additional 1/14 makes 15/14, so your problem is really 15/14 ÷ 3/7.

To divide, you need to multiply by the reciprocal of the divisor, or invert the divisor, 3/7, and multiply. The problem 15/14 ÷ 3/7 is equivalent to 15/14 x 3/7. Cancel before you multiply. Divide both 15 and 3 by 3, and divide 7 and 14 by 7.

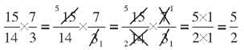
The product 5/2 is an improper fraction, and that’s fine. If you’d rather see it as a mixed number, remember the denominator says the whole was broken into two pieces, broken in halves. You have 5 of those, so you can piece together 2 wholes and have 1 half left.

WORLDLY WISDOM

To quickly convert a mixed number to an improper fraction, multiply the denominator by the whole number and add to the numerator.  To change an improper fraction to a mixed number, divide numerator by denominator and make any remainder the numerator of the fraction. 43/7 = 6 with 1 left over, so 

CHECK POINT

Perform each multiplication or division problem.

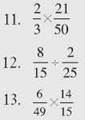
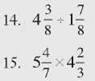
Adding and Subtracting Fractions

Adding and subtracting fractions requires that the fractions have the same denominator. Denominators tell you what kind of things you have, and it’s difficult to even think about adding unless you have the same kind of things, or a common denominator. When you have a common denominator, you simply add the numerators and keep the denominator.  Three of these things plus 7 of these things equals 10 of these same things.

DEFINITION

A common denominator is one that is a multiple of each of the denominators of two or more fractions. The least common denominator is the least common multiple of the denominators.

Your real work comes when the fractions don’t have a common denominator to start out. It’s not impossible to add or subtract fractions with different denominators, but you must change their appearance first. You have to change them to equivalent fractions with a common denominator.

A common denominator is a number that is a multiple of each of the denominators you were given. Ideally, you should choose the lowest number that can be evenly divided by each of the denominators in your equation. That’s called the lowest or least common denominator. Larger multiples will work, but you will have to simplify at the end. Let’s look at some examples.

Suppose you want to subtract 1/3 – 2/7. In order to do this operation, you need to make the denominators of the two fractions match. First, find the lowest common multiple of the two denominators.

The lowest common multiple of 3 and 7 is 21. Multiply 1/3 x 7/7 and 2/7 x 3/3 to change them to fractions with the same value but a different look.

Then you are able to subtract.

Sometimes you’ll look at two denominators and know quickly what number can serve as a common denominator, but if the numbers are large, you may need more of a game plan. To find the lowest common denominator, take a moment first to factor each denominator.

Suppose you need to add 7/30 + 5/42. You look at 30 and 42 and don’t see a common denominator immediately. Think about the factors of each denominator. 30 = 2 x 3 x 5 and 42 = 2 x 3 x 7. Both denominators have factors of 2 and 3, but 30 also has a factor of 5. 42 has a factor of 7. The lowest common denominator will be the product of the 2 and 3 they have in common and the 5 and 7 they don’t.

LCD = 2 x 3 x 5 x 7 = 210

Multiply 7/30 + 7/7, because 30 doesn’t have the factor of 7, and 5/42 x 5/5, because 42 doesn’t have the factor of 5. Give each fraction what it’s missing, then add and simplify.

WORLDLY WISDOM

It is not always necessary to have the lowest common denominator. Sometimes you simply want to add or subtract the fractions as quickly as possible. You can fall back on this strategy. Multiply the two denominators for a common denominator. Multiply the lower right denominator times the upper left numerator and put the result in the upper left numerator's position. Multiply the lower left denominator by the upper right numerator and put the result in the upper right numerator's position. Add or subtract the numerators and simplify if necessary.

You can handle mixed numbers in addition and subtraction by changing them to improper fractions, as you did in multiplication, but you don’t always have to. In addition, you can just combine the fractions and add the whole numbers on to that sum at the end.  is really  so you can rearrange to 

For subtraction, it can be trickier, because there may be regrouping, or borrowing, involved. Try to subtract the fraction parts, and if you can, then you can also just subtract the whole numbers.

If you try subtracting the fractions and realize the first fraction is smaller than the second, you need to borrow from the first whole number. To subtract  you need to borrow 1 from the 8.

CHECK POINT

Complete each addition or subtraction problem.

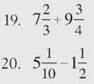
The Least You Need to Know

• To change a fraction to an equivalent form, multiply (or divide) both the numerator and the denominator by the same number.

• To multiply fractions, multiply the numerators, multiply the denominators, and simplify if possible. You may be able to simplify before multiplying by dividing a numerator and a denominator by the same number.

• To divide fractions, invert the divisor and multiply.

• The lowest common denominator of two fractions is the LCM of the two denominators.

• To add or subtract fractions, change each fraction to an equivalent fraction with a common denominator, and add or subtract the numerators. Simplify if possible.