Basic Math and Pre-Algebra

PART 1. The World of Numbers

CHAPTER 7. Ratios, Proportions, and Percentages

We have two basic ways of comparing numbers: an addition/ subtraction method and a multiplication/division method.

The addition/subtraction method makes statements like 15 is 7 more than 8, or 49 is 1 less than 50. The multiplication/ division method compares numbers by saying things like 63 is 3 times as large as 21, or 12 is half of 24.

In this chapter, you’ll focus on that comparison by multiplication and division. You’ll learn to use ratios and extended ratios to help you figure out unknown numbers, and you’ll solve proportions by cross-multiplying. Once you understand percentages, you’ll be able to explore how they’re using in different kinds of problem solving.

Proportional Reasoning

Twice the size, half as many, three times as much. In your daily language, you frequently use the idea of multiplying or dividing as a way to compare numbers. Usually, in conversation, you’ll make the comparison using a simple whole number compared to 1: twice the size or three times as much. Or you might use division in the form of a simple fraction, like half as many. But you could make other comparisons, not always comparing to 1.

If you had two lamps, one 2 feet tall and one 3 feet tall, you could say one is 1.5 times taller than the other, but more often, you’ll stay with the whole numbers and say the taller lamp is to the shorter one as 3 is to 2. Or you could say the shorter lamp is to the taller one as 2 is to 3.

Understanding Ratios and Extended Ratios

A ratio is a comparison of two numbers by division. If one number is three times the size of another, you say the ratio of the larger to the smaller is “3 to 1.” This can be written as 3:1 or as 3 the fraction 3/1. You could also compare the smaller to the larger by saying the ratio is 1 to 3.

DEFINITION

A ratio is a comparison of two numbers by division.

When you are told that the ratio of one number to another is 5:2, you are not being told that the numbers are 5 and 2, but that when you divide the first by the second, you get a number equal to 5/2. This happens when the first number is 5 times some number and the second is 2 times that number. If that’s all you know about the numbers, you have a sense of their relative size, but that’s about all. If you have some other information, you might be able to figure out what the numbers actually are.

Suppose two numbers are in ratio 7:3 and their sum is 50. You know that the first of the numbers you’re looking for is 7 times some number and the other is 3 times that same number, so that they divide to 7/3. With the extra piece of information that they add to 50, you can try to find the numbers by guess and test. If the numbers were actually 7 and 3, they would add to 10. Multiply each one by 2 and you have 14 and 6, which add to 20. A little more experimentation will tell you that 7 x 5, or 35, and 3 x 5, or 15, will add to 50.

That guess and test method can run into some problems. For example, most people won’t guess anything but whole numbers, and the answer won’t always be a whole number, or it might be a very large whole number. Try using a letter, maybe n, called a variable, for the number you don’t know. If the numbers are in ratio 6:5, one is 6n and the other is 5n. If they add to 88, you can say 6n + 5n = 88. That means that 11n = 88, and n must be 8. The numbers are 6 x 8 = 48 and 5 x 8 = 40.

DEFINITION

A variable is a letter or other symbol that takes the place of an unknown number.

An extended ratio compares more than two numbers. Extended ratios are usually written with colons, because you don’t want to put more than two numbers into a fraction. Extended ratios are actually a condensed version of several ratios. If the apples, oranges, and pears in a fruit bowl are in ratio 8:3:2, it means that that the number of apples is 8 times some number, the number of oranges is 3 times that number, and the number of pears is 2 times that number. It also means that the ratio of apples to oranges is 8:3, the ratio of oranges to pears is 3:2 and the ratio of apples to pears is 8:2.

DEFINITION

An extended ratio combines several related ratios into one statement. It is a way to express the ratios a:b, b:c, and a:c in one statement: a:b:c.

Suppose that a smoothie contains pomegranate juice, orange juice, and yogurt, in a ratio of 2:5:3. If you want to make 5 cups of the smoothie to sip throughout the day, how much of each ingredient will you need? If the numbers actually were 2 and 5 and 3, they would add to 10 cups. You need 5 cups, so let’s say 2n cups of pomegranate juice, 5n cups of orange juice, and 3n cups of yogurt, to make a total of 5 cups.

2n + 5n + 3n = 5

10n = 5

n = 1/2

The multiplier is ½, so you need  cup of pomegranate juice,  cups of orange juice, and  cups of yogurt.

MATH TRAP

When you're working with ratios that involve measurements, make sure the units match. If you try to say the ratio of the length to the width of a room is 15 feet to 120 inches, when you go on to use that relationship, you'll be confused about whether your numbers are feet or inches, and you'll likely get the wrong numbers. Make it 15 feet by 10 feet or 180 inches by 120 inches, and your work will be easier and more accurate.

CHECK POINT

1. If the ratio of girls to boys in Math Club is 5:3, and there are 32 members of the club, how many boys are members?

2. The local car dealer sold 40 cars last month. The ratio of gas-powered vehicles to hybrids was 7:1. How many hybrids were sold?

3. The desired ratio of the red roses to white roses in a bouquet is 2:3. If the florist wants the bouquet to have a total of 20 roses, how many white roses and how many red roses will she need?

4. If the ratio of lions to tigers to bears at the zoo is 4:7:4, and there are 45 of these animals all together, how many tigers are there?

5. The ratio of red balloons to white balloons to blue balloons in the auditorium is 21:20:9. If there are 900 balloons in the auditorium, how many are blue?

Solving Proportions

A proportion is a statement that two ratios are equal. The equation 1/3 = 2/6 is an example of a proportion. It says the ratio of 1 to 3 is the same as the ratio of 2 to 6, or, in other words, that the fractions are equal.

When you look at the statement that two ratios are equal as a proportion, you can talk about the four numbers that make up the proportion as the means and the extremes. It’s a little easier to understand which numbers are means and which are extremes and why if you write the ratios with colons, so let’s write 1/3 = 2/6  as 1:3 = 2:6. The extremes are the numbers on the ends, the 1 and the 6. They’re far out. The word mean talks about the middle, so the numbers in the middle, the 3 and the 2, are the means. When you do write it as a pair of equal fractions, it looks like this.

DEFINITION

A proportion is two equal ratios. The means of a proportion are the two middle numbers. The extremes are the first and last numbers.

Proportions can be used to compare things. When you create a proportion, it’s important to be consistent about the order. If you want to say that the ratio of the shortest side of the big triangle to the shortest side of the small triangle is equal to the ratio of their longest sides, be sure that your second ratio is big triangle to small triangle just like the first ratio. If you change the order, the proportion won’t be true.

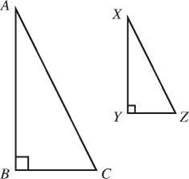
In any proportion, the product of the means—the two middle terms—is equal to the product of the extremes—the first and last terms. For example, in the proportion 5/8 = 15/24, 8 x 15 = 5 x 24. This multiplying of means and extremes is called cross-multiplying. Whenever you have two equal ratios you can cross-multiply, and the two product will be equal. Knowing that will often let you find a number that’s missing from the proportion. You could use a question mark or other symbol to stand for the missing number, but let’s use an x for now.

When you multiply with a variable, especially when you use the variable x, it’s easy to confuse the variable with the times sign x, so you may want to use other ways to write multiplication, like a dot or parentheses. Instead of writing 5 x x, you can write 5∙x or 5(x).

Keep in mind that cross-multiplying can only be done in a proportion. You can cross-multiply when you have two equal ratios, but not in any multiplication with fractions.

DEFINITION

Finding the product of the means and the product of the extremes of a proportion, and saying that those products are equal, is called cross-multiplying.

Suppose you’re told that two numbers are in ratio 7:4, and the smaller number is 14. But what’s the larger number? You can use the means-extremes properties of proportions to help you find out.

If I give you the proportion x/14 = 7/4, you can use cross-multiplying to help you find the value of the number I called x. If you multiply the means you get 4 times the unknown number or 4x. The product of the extremes, 7 x 14, is 98. The product of the means is equal to the product of the extremes, so 4x must equal 98, or 4x = 98. Dividing 98 by 4 tells you that x = 98/4 = 24.5.

WORLDLY WISDOM

When you're cross-multiplying, don't be in a rush to do the arithmetic, especially if your numbers are large. Your work may be easier if you write out the multiplication but don't actually do it. Then when you divide to find the value of the variable, you may see a shortcut. Why do the work of multiplying 42 x 35 if, a moment later, you're going to divide by 21?  Leave the multiplication in factored form, and the division may be easier.

CHECK POINT

Solve the proportion to find the value of the variable.

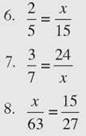
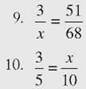
Percent as a Standard Ratio

The word percent means “out of 100.” If you shoot 100 free throws at basketball practice and you sink 60 of them, you made 60 out of 100 shots, or 60 percent. But what if you shot 75 and made 40? What percentage is that? Is that better or worse than 60 percent? You can use proportions to convert any ratio to a percentage. 

DEFINITION

A percentage is a ratio that compares numbers to 100. 42 percent means 42 out of 100, or 42:100. Percentages are sometimes written using the percent symbol, %.

Ratios can be hard to compare if they are “out of” different numbers. Which is larger: 4 out of 9 or 5 out of 12? If you compare them as fractions, 4/9 and 5/12, it might help to change to a common denominator. You could use 36 as the common denominator so 4/9 = 16/36 and 5/12 = 15/36, and you can see that 4/9 is larger. Changing ratios to percentages is like changing fractions to a common denominator. Percentages make it easier to compare different ratios, because they express everything as a part of 100. When you need to change a ratio to a percentage, take your ratio, like 15/20, and set it equal to the ratio P/100. You’re saying 15 is to 20 as P is to 100, or 15 out of 20 is the same as P out of 100. That’s a percentage. Use cross-multiplying to find P.

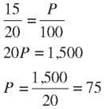
So 15 out of 20 is 75 percent.

The rule you want to remember is “part is to whole as percent is to 100” or   This proportion can be used to solve almost all percent problems. Percentage problems come in three basic types. One type asks a question like “what is 45 percent of 250?” The second type asks “15 is 30 percent of what number?” and the third is “29 is what percentage of 58?” The first type asks you to find the part, the second asks you to find the whole, and the last asks for the percentage.

Suppose your town requires that a candidate receive at least 51% of the vote to be elected mayor. If the population of the town is 1,288, what is the minimum number of votes a candidate must receive to be elected?

You know the percentage and the whole, and you’re looking for the part of the population that is required for election. Start with  Cross-multiply, and you’ll find that the product of the means is 1,288 x 51 = 65,688 and the product of the extremes is 100p. The product of the means is equal to the product of the extremes, so 100p = 65688, and dividing by 100 tells you p = 656.88. (Since no one can cast a fraction of a vote, round this to 657 votes.)

WORLDLY WISDOM

When you use the  rule, the important part is getting the numbers in the right positions. Certain words in the problem can signal this for you. The word “of” usually precedes the whole amount, and the word “is” can generally be found near the part. Some people remember the rule as 

Let’s walk through some examples of the different types of problems. First, finding a percentage.

What percentage of 58 is 22?

Look for “of.” 58 is the whole. Look for “is.” 22 is the part.

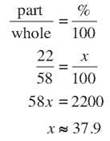
22 is about 37.9 percent of 58.

You might round an answer like that to 38 percent if you don’t want to deal with the decimal. It will depend on the work you’re doing. If you were going to compare two percentages that were both close to 38 percent, you’d want the decimals so you could see which was bigger. If you want to know how much your savings increased, 38 percent is probably just as informative as 37.9 percent.

Let’s look at another example. In this one, you’ll find the whole.

46 is 27% of what number?

Look for “of.” The whole is “what number,” which means it is unknown. Look for “is.” 46 is the part. Both 46 and 27 are near the “is” but 27 has the % sign, so you know it is the percentage.

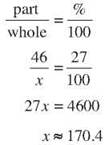
46 is 27% of 170.4, approximately. Again, how much you round will depend on the situation.

One last example before we move on. This one asks you to find the part.

What is 83% of 112?

Look for “of.” 112 is the whole. Look for “is.” “What” is the part, that is, the part is unknown. The percent sign tells you that 83 is the percentage.

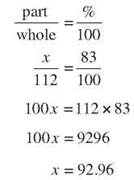
83% of 112 is 92.96. Because that decimal terminates after only two places, you can give the exact answer and not bother with rounding.

If you feel like those examples all seemed very much the same, you’re right. The process is exactly the same: cross-multiply and divide. The difference is the piece that’s unknown, and, of course, the numbers themselves.

Percentages can be greater than 100 percent, and that often happens when you turn a question around. You can say that 2 is 50 percent of 4, or you can reverse the comparison and say 4 is 200 percent of 2. 100 percent is the whole thing, so 200 percent is the whole thing and the whole thing again, or twice as much. The good news is you do the three types of problems exactly the same way even if the percentages are greater than 100 percent.

CHECK POINT

11. 45 is 20 percent of what number?     

12. 16 is what percentage of 64?   

13. What is 15% of 80?

14. 63 is what percentage of 21?

15. What is 120 percent of 55?