Basic Math and Pre-Algebra
PART 2. Into the Unknown
CHAPTER 9. Adding and Subtracting with Variables
The shift from arithmetic to algebra begins with the introduction of variables. Almost immediately, you have to start doing arithmetic with variables. The rules of arithmetic don’t change, but working with one or more unknown quantities requires some new strategies. If you have four 3s, you can do the multiplication and know you have 12, but if you have four x’s, all you can do is say that you have 4x. What 4x is worth depends on what number x stands for.
The statement that you have four x’s, written as 4x, is a simple form of multiplication. As you saw in the last chapter, more complicated multiplication requires multiplying the coefficients, the numbers that tell you how many you have, and multiplying the variables, which usually requires using exponents.
In this chapter, we’ll look at more arithmetic with variables, with a focus on adding and subtracting. I’ll explain when you can, and when you can’t, add or subtract expressions involving variables, and how to do it when you can. And I’ll introduce you to polynomials, a family of expressions built by adding variable terms.
When Are Terms “Like Terms”?
You’re often going to see the word term in this chapter, so let’s start by making sure you understand what it means. A term is a constant, a variable, or an expression involving multiplication of constants and variables. You use the more general word expression to cover just about anything you write using numbers and variables. Terms are a particular subset of expressions that involve only multiplication.
DEFINITION
A term is an algebraic expression made up of numbers, variables, or both that are connected only by multiplication.
Any number on its own is a term. Constants, like 1 or -7, are terms. Any variable, such as x or y, is a term. When you multiply numbers and variables, you get terms like -4y, or xy, or x2, or 18xy2. You can have numbers, variables, numbers and variables multiplied together, and variables multiplied together, which may give you exponents. That’s all okay in a term. You just can’t add or subtract, divide by a variable, or have a variable under a square root sign. Dividing by a constant is the same as multiplying by a fraction, so that’s allowed.
Simplify to Find Terms
It’s possible that an expression may not look at first like it fits the definition of a term, but you might find that you can simplify the expression and the simplified form does fit the definition of term.
For example, the expression 
seems to break all the rules. There’s addition, there’s a variable under a square root sign and there’s division by a variable. But you can do that division. 
so you can make the expression 
Then you might notice that 
5x + 6x is 11x, and that’s a term. Take a minute to think about whether you can simplify an expression before you decide if it fits the definition.
CHECK POINT
Decide if each expression is a term.
1. 4x
2. -12
3. -2t7
4. 6/y
5. a/6
When Can You Combine Terms?
Terms may only involve multiplication, but you need to think about what happens when you want to do something besides multiply, specifically, when you want to add or subtract terms. When the terms are just numbers, addition and subtraction are straightforward: 4 + 8 = 12 and -5 + 9 = 4. You’re just adding (or subtracting) according to the rules of arithmetic. The moment variables enter the picture, however, you’re faced with a dilemma. How do you add two numbers if you don’t know what they are?
You may already have part of the answer. If you add x + x, whatever number x stands for, you have two of that, so 2x. But what if you need to add x + y? You don’t have two x’s and you don’t have 2 y’s. You can’t really say much about what you do have, except that you have x + y.
Different variables, like x and y, are unlike terms. They’re different. It’s an apple-and-orange kind of thing. One apple plus one orange doesn’t give you two apples or two oranges or two appleoranges. It can give you two fruits, if you take a common denominator approach to the matter, but when you’re working with variables, you don’t know enough about them to find a common denominator. You’re stuck admitting that unlike terms can’t be combined.
DEFINITION
Unlike terms are terms with different variables, such as x and y.
In order to combine terms, they must have the same variable. They must be like terms. As usual, there are some complications to that simple rule. What about x + xy? Or x + x2? In each of these examples, the second term has an x, but it also has something else. Can you combine x with xy (which is x multiplied by y) or x2 (which is x multiplied by x)?
If you could combine x and xy, what would it give you? The xy isn’t the same number as x (unless y happens to be 1, and you can’t bet on that) so you don’t have 2x, and you can’t just throw the y away. The terms x and xy are unlike terms.
The x2 may look more like the x, but it’s not the same. If x were equal to 5, x2 would be 25, and they’d add to 30. That’s six times the value of x. But if x were equal to 3, x2 would be 9, and they’d add to 12, which is four times the value of x. There are so many possibilities, and while there is a pattern to them, it’s not immediately clear. It’s difficult to say what x + x2 equals because x and x2 are not like terms.
WORLDLY WISDOM
What is the pattern to x + x2?
If x = 1, x + x2 = 2 or 2x.
If x = 2, x + x2 = 6 or 3x.
If x = 3, x + x2 = 12 or 4x.
Can you see it? The answer is always a multiple of x, and the multiplier is 1 more than the value of x. You can write it like this: x + x2 = (x + 1)x. This is called the factored form of x + x2. If you use the distributive property to multiply x(x + 1), you'll see that it equals x + x2.
Think of it this way: x stands for a number, which we could imagine as the length of a line segment. If x is the length of a line segment, then x2 would be the area of a square whose sides are x units long. Visually, a line segment and a square are very different things. Even though both x and x2 have an x in their names, they’re very different things, different numbers. They’re unlike terms.
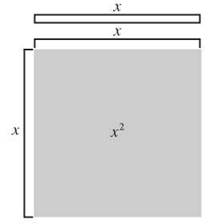
Even though they both contain the same variable, x and x2 represent different ideas. There’s something going on in x2 that’s not happening in the plain x. Visually, you can think of the x2 expanding into a square, while the x is still a line segment. Numerically, the x2 has multiplication going on that’s not happening in the simple x. The x and the x2 are clearly related, but they’re not the same. They’re not like terms.
Different variables are clearly not alike, but even terms built from the same variable may be different from one another. To be like terms, terms must have the exact same variable and the exact same exponent. Their variable parts are exact matches. Only their coefficients are different. That means 4y3 and -7y3 are like, because they have the same variable and the same exponent. The fact that the 4 and the -7 are different coefficients is okay. The coefficients are just telling you how many you have.
DEFINITION
Like terms are terms that have the same variable, raised to the same power. For example, the terms 4x and 7x are like terms.
CHECK POINT
Label each pair of terms like or
6. 7y2 and 11y
7. 3t2 and 5t
8. 2x and lx
9. -9a2 and -15a3
10. 132x3 and -83x3