Basic Math and Pre-Algebra
PART 2. Into the Unknown
CHAPTER 10. Solving Equations and Inequalities
One Solution or Many?
When you solve an equation, you find the value of the variable that makes the two sides of the equation identical. It’s the one number that makes the statement true. There are more complicated equations for which there is more than one solution. We’re not ready to look at the solution of those equations just yet, but it’s good to know they exist. For example, the equation x2 = 9 has two solutions. If you replace x with 3, you have 32 = 9, which is true, but if you replace x with -3, you get (-3)2 = 9, which is also true. The equation x2 = 9 has two solutions.
There’s another group of problems that are true for more than one value of the variable, and these are a type of problem we are ready to solve. They’re called inequalities because rather than saying “this equals that,” they say, “this is bigger than that,” or “this is smaller than that.” They tell us that the two sides are unequal.
DEFINITION
An inequality is a mathematical sentence that says one expression is greater than another.
The symbol > is read “is greater than,” and the symbol < is read “is less than.” If you add a line under the symbol, you add “or equal to.” So x ≤ 4 says “x is less than or equal to 4,” and y ≤ _3 says “y is less than or equal to -3. If you think about those statements for a minute, you can see that there are many numbers that you could put in place of x to make a true statement. You could say 5 ≥ 4 or 19 ≥ 4 and both would be true. There are many, many more substitutions for x that make true statements—an infinite number of them, in fact.
Equations ask you to find the value for the variable that makes both sides the same. Inequalities ask you to find the values that make one side larger than the other. The solution will be a set of numbers, rather than a single value.
Solving Inequalities
Inequalities can be solved in much the same way as equations, with one important exception. When you multiply or divide both sides of an inequality by a negative number, the direction of the inequality sign reverses. Remember that the positive and negative sides of the number line are mirror images of one another. When you multiply both sides of the inequality by a negative number, you go through the looking glass and things change. On the positive side, 5 is bigger than 4, but flip to the negative side and -5 is smaller than -4.
The rules for solving inequalities are the same as those for solving equations, except for that one step. When you multiply or divide both sides of an inequality by the coefficient of the variable term, you have to make a decision about the inequality sign.
If you divide both sides of an inequality by a positive number, leave the inequality sign as is.
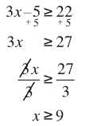
If you divide both sides of an inequality by a negative number, reverse the inequality sign.

CHECK POINT
Solve each inequality.
21. 2x — 5 > 13 + 4x
22. 3x + 2 ≤ 8x + 22
23. 12x + 3 < x + 36
24. 2y - 13 ≥ 4(2 + y)
25. 5x - 10(x - 1) > 95
Picturing the Solution
The solution of an equation is usually just one number, so when you say x = 5, it’s easy to understand what that means. The solution of an inequality is a set of numbers, a collection that goes on and on and includes whole numbers, rational numbers, and irrational numbers. When you write x > 5, you’re describing a whole collection of numbers. It’s helpful to have a picture to understand it.
The solution set of an inequality can be graphed on the number line by shading the appropriate portion of the line. You can graph the inequality x ≥ 2 on the number line by putting a solid dot on 2 and then shading all the numbers to the right of 2.

Start the graph of the inequality x > -4 by circling -4. Don’t fill in that circle, because you don’t actually want -4, but you want everything less than -4. Then shade to the left.
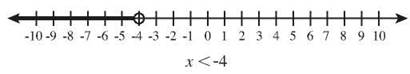
Use an open circle if the inequality sign is > or < and a solid dot for inequalities containing ≤ or ≥.
CHECK POINT
Graph the solution set of each inequality.
26. x > 6
27. t < -1
28. y ≥ -3
29. a ≤ 2
30. x > 0
The Least You Need to Know
• Solve equations by performing the opposite operations in the opposite order.
• Always simplify before trying to solve.
• In an equation, a variable usually represents just one number. In an inequality, a variable usually represents a set of numbers.
• Solve inequalities just like equations, but if you multiply or divide both sides by a negative number, reverse the inequality sign.