Basic Math and Pre-Algebra

PART 3. The Shape of the World

Any world tour must include seeing the sights, having a look at the shape of things. Whether it’s a natural formation like a mountain or a canyon, or a famous building or monument, by the end of a journey, your scrapbook will certainly have some examples of great geometry.

This part of our journey is devoted to looking at the geometry of the mathematical world. You’ll learn the basic vocabulary you need to describe what you see and how to identify the polygons, circles, polyhedrals, and other solids that form the architecture of the mathematical world.

We won’t abandon numbers completely as we look at these shapes, but for a while numbers will be a lesser focus. There’s still a place for calculating, but we’ll investigate relationships between shapes as well.

CHAPTER 12. Basics of Geometry

Geometry begins with a few undefined terms—point, line, and plane—and logically builds a system that describes many physical objects. The word “geometry” means “earth measuring,” and geometry had its beginnings in the work of dividing land up among farmers. Doing that requires lines, angles, and many different shapes.

In this chapter, you’ll lay the foundation on which to build your knowledge of geometry. Starting from those undefined terms, you’ll learn about portions of lines and combining lines to make angles. You’ll measure and classify angles, explore relationships between them, and bisect segments and angles. Parallel and perpendicular lines are the building blocks of many figures and create many angle relationships. Last of all, you’ll take many of these ideas onto the coordinate plane and see how they connect back to algebra.

Points, Lines, Planes, and Angles

The undefined terms of geometry are a curious mix of things you know and things you can only imagine. A point can be thought of as a dot, a tiny spot, or a position. That’s the familiar part. The part that requires imagination is the idea that a point doesn’t take up any space. It has no size and no dimension. You can’t measure it. You can draw a dot to represent a point, even though your dot does take up some space, and you label points with uppercase letters.

You know what a line is. You see lines all the time. But geometry asks you to use your imagination here, too. A line is a set of points—an infinite string of points—that goes on forever in both directions. It has length, in fact it has infinite length, but it has no width and no height. It’s only one point wide or high, and points don’t take up space. And yet, somehow, you can string points together to make something that has infinite length.

People often say, “a straight line,” but in geometry that phrase is redundant. All lines are straight. If it curves or bends, it’s not a line.

When you draw a picture to represent a line, even though your picture does have some width and can’t actually go on forever, you put arrows on the ends to show that it keeps going. You can label the line with one script letter, like line l, or by placing two points on the line and writing those two points with a line over the top, like this: .

DEFINITION

A point is a position in space that has no length, width, or height. A line is a set of points that has length but no width or height. A plane is a flat surface that has length and width but no thickness. Space is the set of all points.

Is your imagination still working? Where do these points and lines live? Where would you draw a point or a line? Perhaps on a sheet of paper or the chalkboard? Those surfaces are the images that help you imagine a plane. A plane is a flat surface that has infinite length and infinite width but no height or thickness. It’s an endless sheet of paper that’s only one point deep.

And where do the points and the lines and the planes live? In space! No, not outer space, at least not exactly. Space, in geometry, is the set of all points, everywhere.

Basic Geometry Terms

Before your imagination is completely exhausted, let’s look at some parts of a line that don’t require so much imagination. A ray, sometimes called a half-line, is a portion of a line from one point, called the endpoint, going on forever in one direction. You can’t measure the length of a ray because, like a line, it goes on forever. A ray looks like an arrow, and you name it by naming its endpoint and then another point on the ray, with an arrow over the top, like this: .

More familiar, if only because it can really fit on your paper is a line segment, literally, part of a line. A line is a portion of a line between two endpoints. (Finally, something you can measure!) Name it by its endpoints, with a segment over the top, like this: .

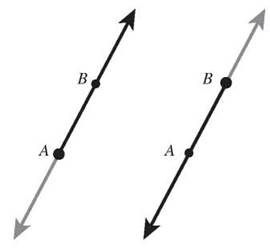
Lines contain infinitely many points, but they are named by any two points on the line. A line that contains the two points A and B can be named  or . In the same way, a line segment can be named by its endpoints in either order, but for rays, the order makes a difference. The rays  and  are shown and are two different rays.

DEFINITION

A ray is a portion of a line from one endpoint, going on forever through another point.

A line segment is a point of a line made up of two endpoints and all the points of the line between the endpoints.

When you put two rays together, you create a new figure called an angle. An angle is a figure formed by two rays with a common endpoint, called the vertex. The two rays are the sides of the angle. You’ll often see angles whose sides are line segments, but you can think of those segments as parts of rays. (By the way, you can measure angles, too.)

DEFINITION

An angle is two rays with a common endpoint, called the vertex. The rays are the sides of the angle.

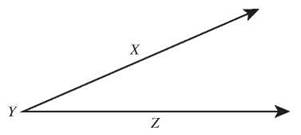
In the angle ∠XYZ, the vertex is Y, and the sides are rays  and . You can name angles by three letters, one on one side, the vertex, and one on the other side. ∠XYZ and ∠ZYX are both names for this angle. An angle can be named by just its vertex, for example, ∠Y, as long as it is the only angle with that vertex.

CHECK POINT

Draw and label each figure described.

1. Line segment           

2. Ray                         

3. Angle ∠DEF

4. Rays  and 

5. Angles ∠PQR and ∠RQT

Length and Angle Measure

Well, you found things you can measure: a line segment or an angle. They don’t go on forever. You can measure them and actually stop somewhere. So how do you do it?

Measuring just means assigning a number to something to give an indication of its size. The number depends on the ruler you’re using. Feet? Inches? Centimeters? Furlongs? They all measure length (although you don’t see furlongs used much outside of horse racing).

A ruler is just a line or line segment that you’ve broken up into smaller segments, all the same size, and numbered. You could even use a number line, and many times we will.

If you place a ruler next to a line segment, each endpoint of the segment will line up with some number on the ruler (even if it’s one of the little fraction lines in between the whole numbers).

The numbers that correspond to the endpoints are called coordinates, and the length of the line segment is the difference between the coordinates. Technically, the length is the absolute value of the difference, because direction doesn’t matter.

DEFINITION

A ruler is a line or segment divided into sections of equal size, labeled with numbers, called coordinates, used to measure the length of a line segment.

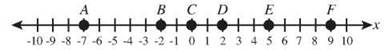
A number line like this can be used to measure line segments.

For example, the length of line segment AB is equal to the distance between coordinates -7 and -2, or five units.

You can also measure angles. Angles are measured by the amount of rotation from one side to the other. Picture the hands of a clock rotating, creating angles of different sizes. It is important to remember that the lengths of the sides have no effect on the measurement of the angle. The hands of the famous clock known as Big Ben are much longer than the hands of your wrist watch or alarm clock, but they all make the same angle at 9 o’clock.

So how do you put a ruler on an angle? For starters, it’s not a ruler. A ruler is a line you use to measure parts of lines. Angles aren’t parts of lines. They’re more like wedges from a circle. So to measure them you create an instrument called a protractor, a circle broken into 360 little sections, each called a degree.

In geometry, angles are measured in degrees. When you put the protractor over the angle with the center of the circle on the vertex of the angle, the sides fall on numbers, called coordinates. The measure of the angle is the absolute value of the difference of the coordinates.

DEFINITION

A protractor is a circle whose circumference is divided into 360 units, called degrees, which is used to measure angles.

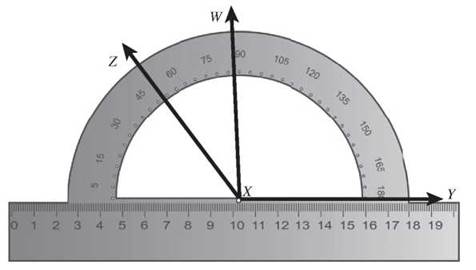
A protractor can be created using any circle, but most people are familiar with the plastic half-circle tool shown here.

When two segments have the same length, they are called congruent segments. In symbols, you could write  to say that the segment connecting A to B is the same length as the segment connecting X to Y. You could also write AB = XY to say the measurements—the lengths—are the same. With the little segment above the letters, you’re talking about the segment. Without it, you’re talking about the length, a number. Segments are congruent. Lengths are equal.

DEFINITION

Two segments are congruent if they are the same length. Two angles are congruent if they have the same measure.

The same is true of angles and their measures. The symbol ∠A refers to the actual angle, and the symbol m∠A denotes the measure of that angle. If you write ∠XYZ ≅ ∠RST, you’re saying the two angles have the same measure. You could also write m∠XYZ = m∠RST. Angles are congruent; measures are equal.

A full rotation all the way around the circle is 360°. Half of that, or 180°, is the measure of a straight angle. The straight angle takes its name from the fact that it looks like a line.

An angle of 90°, or a quarter rotation, is called a right angle. If one side of a right angle is on the floor, the other side stands upright. Angles between 0° and 90° are called acute angles.

Angles whose measurement in greater than 90° but less that 180° are obtuse angles.

DEFINITION

A straight angle is an angle that measures 180°. A right angle is an angle that measures 90°.

An angle that measures less than 90° is an acute angle. An obtuse angle is an angle that measures more than 90° but less than 180°.

You can classify angles one by one, according to their size, but you can also label angles based on their relationship to one another. Sometimes the relationship is about position or location or what the angles look like. Other times it’s just about measurements.

Two angles whose measurements total to 90° are called complementary angles. If two angles are complementary, each is the complement of the other.

The complement of an angle of 25° can be found by subtracting the known angle, 25°, from 90°. 90° - 25° = 65°, so an angle of 25° and an angle of 65° are complementary. To find the measure of the complement of an angle of 12°, subtract 90° - 12° = 78°. An angle of 12° and an angle of 78° are complementary angles.

Two angles whose measurements total to 180° are called supplementary angles. If two angles are supplementary, each is the supplement of the other.

DEFINITION

Complementary angles are a pair of angles whose measurements total 90°.

Supplementary angles are a pair of angles whose measurements total 180°.

To find the supplement of an angle of 132°, 180° - 132° = 48°. The measure of the supplement of an angle of 103° is 180 - 103 = 77°.

When two lines intersect, the lines make an X and four angles are formed. Each pair of angles across the X from one another is a pair of vertical angles. Vertical angles are always congruent; they always have the same measurement.

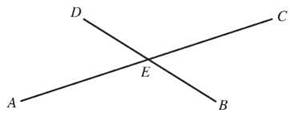
The angles ∠AED and ∠CEB are vertical angles, as are the angles ∠DEC and ∠AEB.

Two angles that have the same vertex and share a side but don’t overlap are called adjacent angles. Two adjacent angles whose exterior sides (the ones they don’t share) make a line are called a linear pair Linear pairs are always supplementary.

DEFINITION

Vertical angles are a pair of angles both of which have their vertices at the point where two lines intersect and do not share a side.

Adjacent angles are a pair of angles that have the same vertex and share a side but do not overlap one another.

A linear pair is made up of two adjacent angles whose unshared sides form a straight angle.

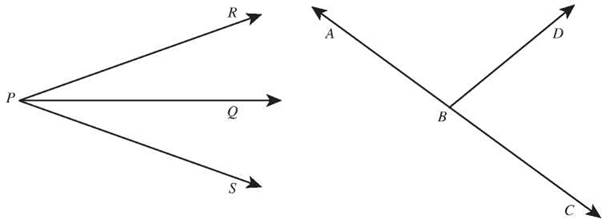
Angles ∠RPQ and ∠SPQare adjacent. Angles ∠ABD and ∠CBD are both adjacent and linear.

CHECK POINT

6. If m∠X = 174°, then ∠X is a(n) ____________ angle.

7. If m∠T = 38°, then ∠T is a(n) ____________.

8. If ∠X and ∠Y are supplementary, and m∠X = 174°, then m∠Y = ____________.

9. If ∠R and ∠T are complementary, and m∠T = 38°, then m∠R = ____________.

10. Lines  and  intersect at point Y. If m∠PYR = 51°, then m∠RYA = ____________, and m∠TYA = ____________.

Midpoints and Bisectors

While you’re in the middle of all these lines and segments and rays and angles, it’s a good time to talk about middles. Because lines and rays go on forever, you can’t talk about the middle of a line or the middle of a ray. To say where the middle of something is, you have to be able to measure it. Until you can assign a length to an object, you can’t say where halfway is.

A midpoint is a point on a line segment that divides it into two segments of equal length, two congruent segments. If M is the midpoint of , then  Each of the little pieces is the same length (AM = MB), and each of them is half as long as . Only segments have midpoints.

A line or ray or segment that passes through the midpoint of a segment is a segment bisector.

Angles don’t have midpoints, but they can have bisectors. An angle bisector is a ray from the vertex of the angle that divides the angle into two congruent angles.

DEFINITION

The midpoint of a line segment is a point on the segment that divides it into two segments of equal length.

A segment bisector is a line, ray, or segment that divides a segment into two congruent segments.

An angle bisector is a line, ray, or segment that passes through the vertex of an angle and cuts it into two angles of equal size.

CHECK POINT

11. M is the midpoint of segment  If PM = 3 cm, MQ= _____ cm and PQ = _____ cm.

12. H is the midpoint of  If XY = 28 inches, then XH = _____ inches.

13. Ray  bisects ∠CAT. If m∠CAT = 86°, then m∠HAT = _____.

14. If m∠AXB = 27° and m∠BXC = 27°, then _____ bisects ∠AXC.

15. m∠PYQ= 13°, m∠QYR = 12°, m∠RYS = 5°, and m∠SYT = 20°. True or False:  bisects ∠PYT.