Basic Math and Pre-Algebra

PART 3. The Shape of the World

CHAPTER 12. Basics of Geometry

Parallel and Perpendicular Lines

Perpendicular lines are lines that intersect at right angles. The symbol for “is perpendicular to” is ⊥, so you can write  to say that segment  is perpendicular to line  If a line, ray, or segment is perpendicular to another segment and also divides that segment into two congruent parts, that line, ray, or segment is the perpendicular bisector of the segment.

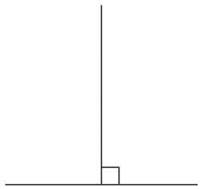
When two lines are perpendicular, all the angles at the intersection will be right angles. When two lines intersect, the vertical angles are congruent, and the adjacent angles are linear pairs, so if one of the angles is a right angle, all four will be right angles.

Perpendicular lines intersect to form right angles, but what about lines that don’t intersect? Lines in the same plane that are always the same distance apart and therefore never intersect are called parallel lines. You see parallel lines all the time: the edges of windows and doors, the lines on a sheet of notebook paper, and railroad tracks are all parallel.

DEFINITION

Lines, rays or segments that meet to form a right angle are perpendicular.

Parallel lines are lines on the same plane that never intersect.

Parallel lines all by themselves are not all that interesting. They just keep on going, never meet, and don’t do anything exciting. When other lines get mixed up with parallel lines, however, some more interesting things do happen.

The Defining Angles

When parallel lines are cut by another line, called a transversal, eight angles are formed. Different pairs from this group of eight are classified in different ways.

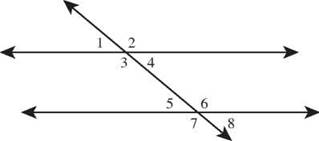
As the transversal crosses the first line, it creates a cluster of four angles, labeled ∠1, ∠2, ∠3, and ∠4 in this picture. As it crosses the second line, it creates another cluster of four angles, labeled∠5, ∠6, ∠7, and ∠8. In each cluster, there is an angle in the upper left position (∠1 from the top cluster or ∠5 from the bottom). There are also angles in the upper right, lower left, and lower right positions. The angle from the upper cluster and the angle from the lower cluster that are in the same position are called corresponding angles.

DEFINITION

A transversal is a line that intersects two or more other lines.

Corresponding angles are a pair of angles created when a transversal intersects two parallel lines that are on the same side of the transversal and are both above or both below the parallel lines.

When parallel lines are cut by a transversal, corresponding angles are congruent. They have the same measurements. ∠1 ≅ ∠5, ∠2 ≅ ∠6, ∠3 ≅ ∠7, and ∠4 ≅ ∠8.

Look at only the angles that are between the parallel lines, ∠3, ∠4, ∠5, and ∠6. Choose one from the top cluster, say ∠3, and the one from the bottom cluster on the other side of the transversal, ∠6, and you have a pair of alternate interior angles. Take one angle from each side of the transversal so that they are not between the parallels but outside them, like ∠1 and ∠8 or ∠2 and ∠7, and you have a pair of alternate exterior angles. Alternate exterior angles are congruent if the lines are parallel.

DEFINITION

Alternate interior angles are two angles formed when a transversal intersects parallel lines that are on opposite sides of the transversal and between the parallel lines.

Alternate exterior angles are two angles formed when a transversal intersects parallel lines that are on opposite sides of the transversal and outside the parallel lines.

When parallel lines are cut by a transversal, alternate interior angles are congruent. They have the same measurements. ∠3 ≅ ∠6 and ∠4 ≅ ∠5.

Using these facts about parallel lines and corresponding angles and alternate interior angles, and the fact that vertical angles are congruent, you can figure out that ∠1 ≅ ∠4 ≅ ∠5 ≅ ∠8 and ∠2 ≅ ∠3≅ ∠6 ≅∠7. Add the fact that ∠1 and ∠2 are supplementary, and it becomes possible to assign each of the angles one of two measurements. ∠1, ∠4, ∠5, and ∠8 have one measurement, and ∠2, ∠3, ∠6, and ∠7 are supplementary to those. If you know the measurement of one angle created when a transversal cuts parallel lines, you can find the measurements of all eight angles. If m∠1 is 40°, then ∠4,∠5, and ∠8 are also 40°, and the other four angles are 180 ° - 40° = 140°.

CHECK POINT

Lines  and  are parallel. Transversal  intersects  at X and  at Y.

16. ∠PXY and ∠XYT are a pair of _______ angles.

17. ∠AXQ and ∠XYT are a pair of _______ angles.

18. If m∠XYT = 68°, then m∠PXA = _______.

19. If m∠PXY = 107°, then m∠RYB = _______.

20. If  ⊥ , then m∠XYR = _______.

Slopes

Geometry and algebra may feel like different worlds at times, but now and then, they come together, and that often happens on the coordinate plane. When we looked at graphing linear equations, you saw how the slope of a line controlled its tilt or angle. When you talk about parallel and perpendicular lines, the angles the lines make are important.

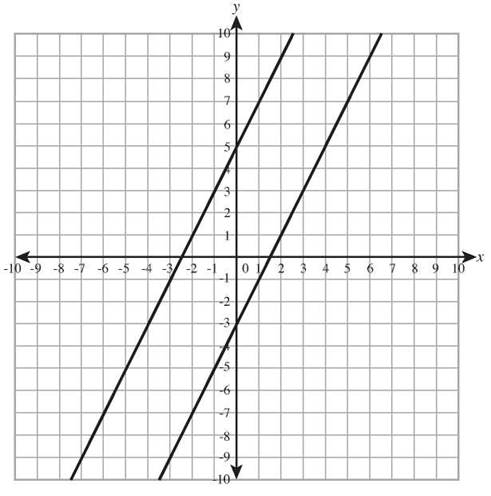
The graphs of two lines in the coordinate plane will be parallel lines if they have the same slope. The matching slopes mean they run at the same angle and don’t tilt toward each other, so they never cross. The line y = 2x - 3 and the line y = 2x + 5 both have a slope of 2, and so they will be parallel.

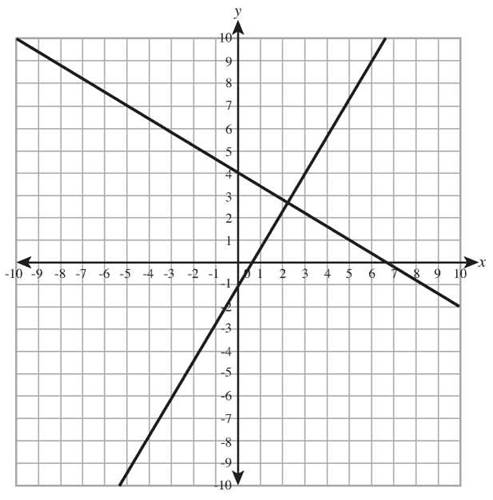
In order for the graphs of two linear equations to be perpendicular lines, one must rise and one must fall, so the slopes must have opposite signs. That alone won’t get that exact right angle, however. To actually be perpendicular, the lines must have slopes that are negative reciprocals. If one line has a slope of 2, a line perpendicular to it will have a slope of -1/2. The graphs of  and  are perpendicular lines because their slopes, -3/5 and 5/3, multiply to -1, so they are negative reciprocals.

CHECK POINT

Label each pair of lines as parallel, perpendicular, or neither.

21. Line a has a y-intercept of 2 and a slope of -3. Line b has a j-intercept of -1/2 and a slope of -3.

22. Line  has a slope of 3/5 and a y-intercept of -4. Line  has a slope of -5/3 and a y-intercept of 2.

23. The equation of line p is y = 2x - 5, and the equation of line q is y = 5x - 2.

24. Line  and line  if X is the point (4,-2), Y is (7,6), W is (2,-8), and Z is (0, 4).

25. The line 3x – 2y = 12 and the line 2x + 3y = 12.

The Least You Need to Know

•  Midpoints and bisectors divide segments into two congruent segments; angle bisectors divide angles into two congruent angles.

•  Angles less than 90° are acute, angles greater than 90° are obtuse. Right angles are 90°, and straight angles are 180°.

•  Complementary angles are two angles that add to 90°, and supplementary angles are two angles that add to 180°.

•  Vertical angles are congruent; linear pairs are supplementary.

•  Parallel lines never intersect; perpendicular lines intersect at right angles.

•  If parallel lines are cut by a transversal, pairs of corresponding angles, alternate interior angles, or alternate exterior angles are congruent.