Basic Math and Pre-Algebra

PART 1. The World of Numbers

CHAPTER 2. Arithmetic

The last chapter focused on the world of numbers and how to express those numbers in words and symbols. The next step is investigating how to work with numbers. In other words, it’s time to look at arithmetic.

The two fundamental operations of arithmetic are addition and multiplication (and multiplication is actually a shortcut for repeated addition). Subtraction and division are usually included in the basics of arithmetic, but you’ll see that these are really operations that reverse on addition and multiplication. We’ll look at the basics of skillful arithmetic and introduce some strategies that may make the work easier.

Addition and Subtraction

The counting numbers came to be because people needed to count. Soon thereafter, people started putting together and taking apart the things, or groups of things, they had counted. If you have 3 fish and your best buddy has 5 fish, you have a pretty satisfying meal (unless you invite 20 friends, but that’s division and that’s later). You could put all the fish in a pile and count them again, but soon you get the notion of 3 + 5 = 8. And if you only eat 4 fish, again, you could count the fish that are left, but before too long, you grasp subtraction: 8 - 4 = 4. Addition and subtraction are just ideas of putting together and taking away that people developed to avoid having to keep recounting.

Addition

If addition is just a substitute for counting, why do you need it? The need is speed, especially when the numbers get large. Counting 3 fish and 5 fish to find out you have 8 fish is fine, but counting 3,000 fish and 5,000 fish would not be practical. When the addends, the numbers you’re adding, get larger, you need a system to find the sum, or total, quickly. The place value system allows you to add large numbers in a reasonable amount of time.

DEFINITION

A sum is the result of addition. The numbers that are added are called addends. In the equation 5 + 10 = 15, 5 and 10 are addends, and 15 is the sum.

It’s important, of course, to learn basic addition facts, but the facts in the table and an understanding of our place value system will get you through most addition problems.

Basic Addition Facts

The left column and top row show the digits from 1 to 9. The box where a row and column meet contains the sum of those digits.

When you add 3 + 5, you get 8, a single digit. That could be adding 3 ones and 5 ones to get 8 ones, but 3 thousands + 5 thousands make 8 thousands, so the same addition could be done for larger addends. It’s just about writing the digits in the proper places.

When you add numbers with more than one digit, stack them one under the other, with the decimal points aligned (even if the decimal points are unseen.) To add 43,502 and 12,381, you write them like this:

This puts the ones under the ones, the tens under the tens, the hundreds under the hundreds, and so on. You just have to add the digits in each place, starting on the right with the ones place:

2 ones + 1 one equals 3 ones 0 tens + 8 tens equals 8 tens

5 hundreds + 3 hundreds equals 8 hundreds

3 thousands + 2 thousands equals 5 thousands

4 ten-thousands + 1 ten-thousand equals 5 ten-thousands

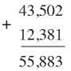
It’s traditional to start from the right, from the lowest place value, and work up. There are problems, like this one, which could be done left to right, but in the next example, you’ll see why right to left is the better choice. The key is that in the previous example, each time you added two digits, you got a single digit result. That’s not always the case. Let’s change just one digit in that problem. Change 43,502 to 43,572.

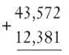
Now when you add the ones digits you get a single digit, 3, which goes in the ones place of the answer, but when you add the 7 tens to the 8 tens, you get 15 tens, and there’s no way to squeeze that two-digit 15 into the one space for the tens digit. You have to regroup, or as it’s commonly called, you have to carry.

Our 15 tens can be broken up into one group of 10 tens and one group of 5 tens. The group of 10 tens makes 1 hundred. You’re going to pass that 1 hundred over to the hundreds place, to the left, and just put the 5, for the remaining 5 tens, in the tens digit place. You put the 5 in the tens place of the answer, and place a small 1 above the hundreds column to remind yourself that you’ve passed 1 hundred along. In common language, you put down the 5 and carry the 1.

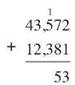
When you add the hundreds digits, you add on that extra 1. Five hundreds + 3 hundreds + the extra 1 hundred from regrouping = 9 hundreds.

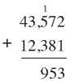
As you finish the addition in the other columns, you’ll find that each gives you just one digit, so no further regrouping or carrying is needed.

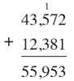
A problem may not need regrouping at all, like our first example, or just once, like this example, or many times, or even every time. Say you want to add 9,999 and 3,457.

In the ones place, 9 + 7 = 16. Put down the 6 and carry the 1. In the tens, 9 + 5 + 1 you carried = 15. Put down the 5 and carry the 1. In the hundreds, 9 + 4 + 1 you carried = 14. Put down the 4 and carry the 1. In the thousands, 9 + 3 + 1 you carried = 13.

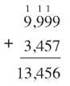
CHECK POINT

Find each sum.

1. 48 + 86

2. 97 + 125

3. 638 + 842

4. 1,458 + 2,993

5. 12,477 + 8,394

Adding Longer Columns

Addition is officially a binary operation. That means that it works with two numbers at a time.

In fact, all four arithmetic operations (addition, subtraction, multiplication, and division) are binary operations, but for addition (and multiplication) it is possible to chain a series of operations together. When you add 4 + 9 + 7 + 5, you’re actually only adding two numbers at a time.

You add 4 + 9 to get 13, then that 13 + 7 to get 20, and then 20 + 5 to get 25. The same kind of chaining works with larger numbers, as long as you remember to stack the numbers so that decimal points, and therefore place values, are lined up.

Suppose you wanted to add 59,201 + 18,492 + 81,002 + 6,478. First, stack them with the (invisible) decimal points aligned.

Add each column, regrouping and carrying over to the next place if you need to. Chain the addition in each column. In the ones column, you’re adding 1 + 2 + 2 + 8, so 1 + 2 is 3, 3 + 2 is 5, and 5 + 8 is 13. Put the 3 in the ones column of the answer and carry the 1 ten to the tens column.

Add the tens column. 0 + 9 + 0 + 7 + the 1 you carried is 17, so put down the 7 and carry the 1.

Keep the chain of additions going, column by column, and don’t be alarmed when the thousands column adds to 25. Just put down the 5 and carry a 2 over to the ten-thousands column.

There are a lot of little steps in an addition like this, and you may wonder why some people are so quick at it while others take more time. The answer probably has to do with the order in which those speedy folks do the job.

You can only add two numbers at a time, but you don’t have to add them in the order they’re given to you. There are two properties of addition that help to simplify and speed up your work. They’re called the commutative property and the associative property.

The commutative property tells us that order doesn’t matter when adding. It doesn’t take long to realize that 4 + 7 is the same as 7 + 4, and the same is true for any two numbers you add.

If you add 3,849,375 + 43,991, you’ll probably put the 3,849,375 on top and the 43,991 under that, because that’s the way it was given to you, but you’d get exactly the same answer if you did it with the 43,991 on the top.

It’s important to remember that not every operation has this property. If you have $1,000 in the bank and withdraw $100, no one at the bank will blink, but if you have $100 and try to withdraw $1,000, there’s likely to be an unpleasant reaction. Withdrawing money from your bank account is a subtraction, and subtraction isn’t commutative.

DEFINITION

The commutative property is a property of addition or multiplication that says that reversing the order of the two numbers will not change the result.

The other useful property of addition is the associative property. This property tells us that when adding three or more numbers, you can group the addends in any combination without changing the outcome.

For example, when adding 8 + 5 + 5 + 2, you might decide that adding those two 5s first is easier than going left to right. The associative property says you can do that without changing the result. You can take 8 + 5 + 5 + 2, add the two 5s first, and make the problem 8 + 10 + 2. That will give you 20, which is the same answer you would have gotten going left to right.

DEFINITION

The associative property is a property of addition or multiplication that says that when you must add or multiply more than two numbers, you may group them in different ways without changing the result.

If a problem has lots of numbers, you’ll sometimes see parentheses around some of the numbers. This is a way of saying “do this part first.” It might have 3 + (7 + 4) + 9 to tell you to add the 7 and the 4 first. That can be helpful, and sometimes absolutely necessary, but the associative property says that if the problem is all addition or all multiplication, you can move those parentheses. It’s telling you that you’ll get the same answer no matter which part you do first, as long as the problem has just one operation, addition or multiplication. 3 + (7 + 4) + 9 = (3 + 7) + 4 + 9. You can regroup.

When you let yourself use both the commutative and the associative properties, you realize that as long as addition is the only thing going on, you can tackle those numbers in any order. That’s one step toward speedier work. If you can add any two numbers at a time, do the simple ones first. Adding 8 + 5 + 5 + 2 is easier if you rearrange it to 5 + 5 + 8 + 2. Add the 5s to get 10, add the 8 + 2 to get another 10, and the two 10s give you 20.

MATH TRAP

Like the commutative property, the associative property is for addition (or multiplication), not for subtraction (or division) and not for combinations of operations. (8 + 7) + 3 is the same as 8 + (7 + 3), but (8 + 7) x 3 is not the same as 8 + (7 x 3).

Grouping the numbers in this way is easier because 5 and 5 are compatible numbers, and so are 8 and 2. Compatible numbers are pairs of numbers that add to ten. Why ten? Because our decimal system is based on tens. You might have your own version of compatible numbers, which add to something else.

For example, if you were a shepherd and had to keep track of a flock of seven sheep, you’d spend a lot of your time counting to seven to be sure you had them all. You’d quickly get to know that if you saw 5 of them in the pasture and 2 on the hill, all was well. If 3 were by the stream and 4 under the tree, you were good. You’d know all the pairs of numbers that added to 7: 1 + 6, 2 + 5, and 3 + 4. For general addition purposes, however, compatible numbers are pairs that add to 10: 1 + 9, 2 + 8, 3 + 7, 4 + 6, and 5 + 5.

Looking for compatible numbers, and taking advantage of the associative and commutative properties, can speed up addition. Adding 4 + 9 + 5 + 7 + 8 + 9 + 2 + 3 + 6 + 5 + 1 just as written could be tedious. But if you look for compatible numbers and rearrange, it’s not too bad.

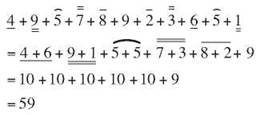
If you use these tactics on each place value column, even long addition problems can go quickly. Take a look at the following addition problem.

In the ones column, you can find 2 + 8 and 1 + 9 and another 5 to make 25. Put down the 5 and carry the 2. In the tens, there’s a 3 + 7 and an 8 + 2 (that you carried) and another 9 for 29. Put down the 9 and carry the 2. In the hundreds, you’ll find 7 + 3, 4 + 6 and 8 + 2 for a total of 30. Put down the 0 and carry 3. There are two pairs that make 10 in the thousands, plus another 9, and the ten-thousands will add to 16.

CHECK POINT

Use compatible numbers to help you complete each addition problem.

6. 18 + 32 + 97               

7. 91 + 74 + 139             

8. 158 + 482 + 327 + 53

9. 71,864 + 34,745 + 9,326

10. 9,865 + 7,671 + 8,328 + 1,245 + 3,439

Subtraction

Subtraction is often thought of as a separate operation, but it’s really a sort of backward addition. It’s how you answer the question, “What do you add to A if you want to have B?” What do you add to 13 to get 20? Well, 20 - 13 is 7, which means 13 + 7 is 20. In this example, 7 is the difference between 20 and 13.

Subtraction and addition are inverse operations. Remember that shepherd who knows all the pairs that add to 7? If he looks up and only sees 5 sheep, he needs to know how many sheep are missing. His question can be phrased in addition terms as 5 + how many = 7? Or you can write it as a subtraction problem: 7 - 5 = how many? Either way you think about it, compatible numbers will be helpful with subtraction as well as addition.

DEFINITION

The result of a subtraction problem is called a difference. Officially, the number you start with is the minuend, and the number you take away is the subtrahend, but you don't hear many people use that language. In the equation 9 - 2 = 7, 9 is the minuend, 2 is the subtrahend, and 7 is the difference.

An inverse operation is one that reverses the work of another. Putting on your jacket and taking off your jacket are inverse operations. Subtraction is the inverse of addition.

The “take-away” image of subtraction thinks of the problem as “if you have 12 cookies, and I take away 4, how many cookies are left?” That works fine for small numbers, and when you’re working with large numbers, you can apply it one place value column at a time. In the following subtraction problem, you can work right to left:

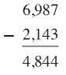
7 ones take away 3 ones equals 4 ones

8 tens take away 4 tens equals 4 tens

9 hundreds take away 1 hundred equals 8 hundreds

6 thousands take away 2 thousands equals 4 thousands

Things get a little more complicated when you try a subtraction like 418 - 293. It starts out fine in the ones place: 8 - 3 = 5. But when you try to subtract the tens column, you have 1 - 9, and how can you take 9 away from 1? This is when you need to remember—and undo—the regrouping you did in addition.

In the process of addition, when the total of one column was more than one digit, too big to fit in that place, you carried some of it over to the next place. So when you’re subtracting —going back—and you bump into a column that looks impossible, you’re going to look to the next place up and take back, or borrow, so that the subtraction becomes possible.

In our example of 418 - 293, you’ll look to the hundreds place of 418, where there are 4 hundreds, and you’ll borrow 1 hundred. You’ll cross out the 4 and make it a 3, so you don’t forget that you borrowed 1 hundred, and you’ll take that 1 hundred and change it back into 10 tens. You’ll add those 10 tens to the 1 ten that was already in the tens place, and you’ll have 3 hundreds, 11 tens, and 8 ones. Then you can take away 293, or 2 hundreds, 9 tens, and 3 ones. So 8 ones - 3 ones = 5 ones, 11 tens - 9 tens = 2 tens and 3 hundreds - 2 hundreds = 1 hundred. Here’s how it would look:

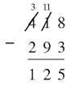
Borrowing isn’t always necessary, as you saw in the earlier example. When it is, you’ll find it’s wise to mark the ungrouping you’ve done and not try to juggle it all in your head.

CHECK POINT

Complete each subtraction problem.

11. 596 - 312

12. 874 - 598

13. 1,058 - 897

14. 5,403 - 3,781

15. 14,672 - 5,839

Thinking of subtraction as adding back instead of taking away can be helpful for mental math. If you buy something that costs $5.98 and give the cashier a $10 bill, how much change should you get? Instead of doing all the borrowing and regrouping that’s necessary to subtract 10.00 - 5.98, start with $5.98 and think about what you’d need to add to get to $10. You’d need 2 pennies, or $0.02, to make $6, and then another $4 to make $10. So your change should be $4.02.

You can use the add-back method of subtraction whenever it seems convenient, even if you’re not making change. To subtract 5,250 - 3,825, you can start with 3,875 and think:

Adding 5 will make 3,830

Adding 20 will make 3,850

Adding 400 will make 4,250

Adding 1,000 will make 5,250

So 5,250 - 3,825 = 1,425.

CHECK POINT

Subtract by adding back.

16. 100 - 62

17. 250 - 183

18. 500 - 29

19. 400 - 285

20. 850 - 319