Basic Math and Pre-Algebra

PART 3. The Shape of the World

CHAPTER 14. Quadrilaterals and Other Polygons

Rhombuses and Squares

A rhombus is a parallelogram with four sides of the same length, an equilateral parallelogram. Because the rhombus is a parallelogram, it has all the properties of a parallelogram, and it still may have that lean to one side, if its angles are different sizes. It’s an equilateral parallelogram, but not always an equiangular one.

A square is a parallelogram that is both a rhombus and a rectangle. Squares have four right angles and four equal sides. They are equilateral and equiangular.

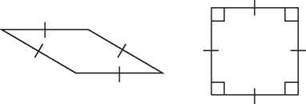
A rhombus is a parallelogram in which all sides are congruent. A square is a parallelogram with four congruent sides and four right angles.

In a rhombus or a square, drawing one diagonal will make two congruent triangles, just as it does in any parallelogram. In a rhombus, those triangles will be isosceles, and in a square, they will be isosceles right triangles. You know that in 45-45-90 right triangles the length of the hypotenuse is the length of a leg times the square root of two. That means that the length of the diagonal of a square will be the length of a side times radical two. Because the square is a rectangle, both diagonals are the same length.

When you draw both diagonals in a rhombus or a square, a bunch of things happen. The diagonals bisect each other, just as they do in any parallelogram. Because the sides of the rhombus (or square) are all the same length, you can figure out that the diagonals of any rhombus, including a square, are perpendicular to one another.

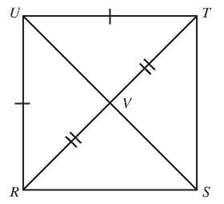
In RSTU, RU = UT, RV = VT, and UVequals itself, so ∆RVU and ∆TVU match each other. That means ∠RYU is congruent to ∠TVU, but they’re also supplementary, so they must both be 90°. If the diagonals cross at right angles, they’re perpendicular.

CHECK POINT

For each quadrilateral described, choose the best label from parallelogram, rectangle, rhombus, or square.

6. In quadrilateral FORT,  and 

7. In quadrilateral CAMP, CA = AM = MP = CP and 

8. In quadrilateral VASE, diagonals  and  are congruent, but sides  and  are not.

9. In quadrilateral SOAP,  and 

10. In quadrilateral COLD, diagonals  and  are perpendicular bisectors of one another, but they are not congruent.