Basic Math and Pre-Algebra

PART 3. The Shape of the World

CHAPTER 14. Quadrilaterals and Other Polygons

Area of Quadrilaterals

The area of a quadrilateral is a little trickier to calculate than the perimeter, but once you know a few formulas, it’s not hard at all. The area of any parallelogram is found by multiplying the base times the height (A = bh). In a triangle, the height must be measured as the perpendicular distance between a vertex and the base. In a parallelogram, the height is the perpendicular distance between two bases.

MATH TRAP

Don't confuse the perpendicular, so rectangles, where side with the height. In most parallelograms, the sides are not you can't use a side as a height. The exception, of course, is the sides do meet at right angles.

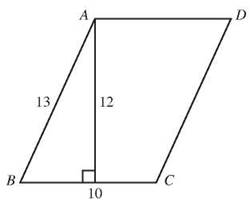
To find the area of parallelogram ABCD, it’s not enough to know that AB = 13 meters and BC = 10 meters. You could use either of those measurements as the base, but neither of them is a height. You need to know the perpendicular distance between two bases. If you know that the height, drawn to BC, is 12 meters, then you can find that the area is 12 x 10 or 120 square meters.

WORLDLY WISDOM

Remember that area is always measured in square units. That's because you multiply a length in units (such as inches, feet, or meters) by another length in the same units. Units multiplied by units equals units squared, or square units.

That area formula of base times height (A = bh) will work for any parallelogram, including rectangles, rhombuses, and squares. But there are other area formulas, specific to those special parallelograms, which may be useful from time to time. Some are just another way of saying things. Because a rectangle has adjacent sides that are perpendicular, the sides, usually called the length and the width, are the base and the height, so you see the formula for the area of a rectangle as A = L x W. The formula for the area of a square is special, because it is a rectangle, so you could use A = L x W, but all four of its sides are the same length, so the formula becomes A = s².

WORLDLY WISDOM

The habit of referring to the exponent 2 as “squared” comes from the fact that the area of a square is the length of a side to the second power.

Let’s look at a story problem using area.

Suppose you want to buy carpet for a room that measures 15 feet by 20 feet. The room is a rectangle, so you multiply 15 by 20 and go to the carpet store, knowing you need 300 square feet of carpet. When you arrive, you find that carpet is sold by the square yard, not the square foot. What now?

You have two choices. Your first option is to start over and figure out the measurements of your room in yards instead of feet. You know there are 3 feet in a yard, so 15 ÷ 3 = 5 yards and 20 ÷ 3 = yards. Then you can multiply 5 by to find out you need square yards.

Your second option is to take your 300 square feet and divide by the number of square feet in a square yard. A square yard is a yard times a yard, or 3 feet times 3 feet, so it’s 9 square feet. Your 300 square feet divided by 9 is square yards. In both cases, you arrived at the same answer.

MATH TRAP

To get units squared, you need to multiply units by units, that is, feet times feet or meters times meters. But if you don't pay attention to whether the units match, you could be multiplying feet times inches, and that doesn't give you square feet or square inches. It just gives you the wrong answer. Make sure your units match.

The rhombus is usually thought of as the most unusual parallelogram, and its area formula is the most different from the others. It’s built from the fact that the diagonals divide the rhombus into four congruent right triangles. The area of each right triangle is one-half of the product of its base and height, and it’s a right triangle, so the legs are the base and height. Each leg is half of a diagonal, so if we call the the diagonals d₁ and d₂, the area of each right triangle is Since there are four triangles that make up the rhombus, the area of the rhombus is or one-half the product of the diagonals.

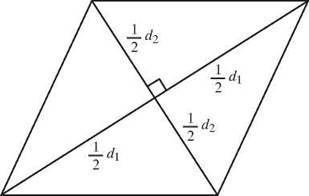
How would you use that formula? Suppose you need to find the area of a rhombus with diagonals 12 cm and 20 cm. You could go through a lot of calculating to try to find the length of the side, but you’d still need the height. Instead, remember that the area of a rhombus is half the product of the diagonals. The area of the rhombus is

So you can use the formula A = bh for all parallelograms if you know the base and the height. That covers the A = LW for the rectangle and the A = s² for the square. You can use the fancy formula for the rhombus if you know the lengths of the diagonals. But what about a trapezoid? It’s not a parallelogram, so your parallelogram formula doesn’t work, but you might need to find its area anyway. How?

Well, it just so happens that if you draw the median of a trapezoid and cut along the median, you can flip the top piece over and set it next to the bottom piece. When you do that, the two pieces will fit together to make a parallelogram.

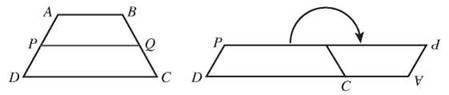
The height of the parallelogram is half the height of the trapezoid. The base of the parallelogram is the sum of the length of the long and the short base of the trapezoid. So the area of a trapezoid is equal to half the height multiplied by the sum of the bases.

WORDLY WISDOM

Some people remember this formula as the average of the bases times the height, or the length of the median times the height.

Try using that formula to figure out the height of a trapezoid with an area of 40 square centimeters and bases 3 cm and 5 cm. Plug those numbers into the formula.

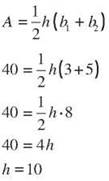
The height of the trapezoid is 10 centimeters.

CHECK POINT

16. Find the perimeter and area of a square with a side of 17 cm.

17. Find the perimeter and area of a rectangle 18 inches long and 9 inches wide.

18. Find the area and perimeter of parallelogram ABCD if AB = CD = 7 inches, AC = BD = 21 inches, and the height from B perpendicular to is 3 inches.

19. Find the perimeter and area of a rhombus with sides 5 inches long if the diagonals measure 6 inches and 8 inches.

20. The area of a parallelogram with a height of 48 cm is 3,600 square centimeters, and its perimeter is 250 cm. Find the lengths of the sides of the parallelogram.