Basic Math and Pre-Algebra

PART 3. The Shape of the World

CHAPTER 15. Circles

Triangles, quadrilaterals, pentagons, hexagons, and all the figures you’ve learned about so far have one thing in common: line segments. All polygons are built from line segments that form their sides and meet to form their angles. But the world of geometry isn’t all straight lines.

Around the world of geometry, you’ll find lots of things that are round, things that curve. The basic shape that forms the basis of all things that curve is the circle. In this chapter, you’ll meet the circle and all the lines and angles that are associated with it. You’ll get to know what those lines tell you about the circle and see how they relate to the familiar triangle. You’ll learn how to measure the angles, and find out how they relate to the circle and to one another. And just as you learned to find the perimeter and area of a polygon, you’ll explore how to measure the distance around a circle and how to measure the space inside it.

The Language of Circles

Take a piece of string and tie a pencil to one end. Pin the other end of the string to the center of a sheet of paper, grab the pencil and pull it out as far as the string will go. With the pencil point on the paper, move the pencil wherever you can, keeping the string taut. The pencil moves around the point where you pinned the string, tracing a curve that comes around to meet itself. That curve is a circle.

A circle is defined as the set of all points at a fixed distance from a given point. The point is called the center of the circle. That’s the spot where you pinned down the string. The fixed distance that determines the size of the circle is called the radius. That’s the length of the string. (The plural of radius is radii.) All radii of a circle are the same length, because every point on the circle is the same distance from the center.

DEFINITION

The collection of all points that sit at a certain distance, called the radius, from a set point, called the center, forms the shape called a circle.

If you mark two or more points on a circle, you divide the circle into sections. Each portion or part of the circle is called an arc. An arc that is less than half the circle is a minor arc. An arc that is greater than half the circle is a major arc. A half circle is called a semicircle.

DEFINITION

An arc is a portion of a circle. A semicircle is half a circle, a minor arc is smaller than a semicircle, and a major arc is larger than a semicircle.

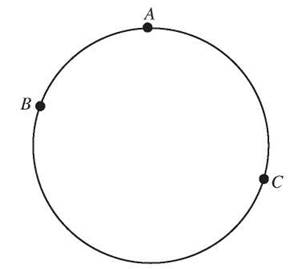
Arcs are named by the points at each end of the arc, with an arc symbol over the top, but that isn’t always enough information. The notation  means the minor arc that is the shorter path along the circle from A to C, but you might want to name the major arc that goes around the circle in the other direction from A to C. To show that you want a major arc, include another letter of a point on the major arc to show which way you want to travel. So  names the major arc from A through B to C.

Most of the units of measurement you use were designed for lines, so when you get to circles, you need a different way of measuring. The type of measuring you want to do in circles is much more like measuring an angle than measuring a line, so you borrow the system of degrees for use in circles. Degrees measure the rotation, how far you turn around a point. A circle turns all the way around its center point until it meets itself again. That full rotation is 360°. There are 360° in a full circle and 180° in a semicircle. Every arc can be assigned a measurement as a number of degrees, according to what part of the circle it is. Minor arcs are less than 180°, and major arcs are more than 180°. A quarter of the circle is one-fourth of 360°, or 90°.

One circle, all by itself, is pretty, but there’s not a lot to say about it. Its center controls where it is, its radius controls how big it is, and it’s always the same shape. If you have two or more circles, they can begin to interact a little bit. You can have two circles that just barely touch each other and have just one point in common. Those are tangent circles.

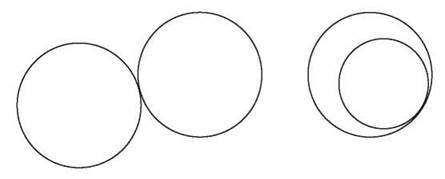
Tangent circles touch at only one point.

One circle can be tangent to another from outside or from inside. If the circles are externally tangent, they can be the same size or different sizes, but to be internally tangent, they’ll have to be different sizes or they’ll just sit right on top of one another. If a smaller circle is placed inside a larger one so that their centers are aligned, they won’t touch each other, but they are concentric circles, circles with the same center.

Concentric circles are circles with the same center.

MATH IN THE PAST

Not every curve is a circle or part of a circle. Ancient mathematicians looked at the different shapes that are seen when a cone is cut. If the cut goes straight across, you see a circle, but if it slants a little, or a lot, you see different shapes. One of them is an oval shape that mathematicians call an ellipse. It's sort of a squashed circle.

CHECK POINT

Complete each sentence.

1. An arc less than half a circle is a _______ arc.

2. The distance from the center point to any point on the circle is called the _______.

3. Two circles with the same center are _______ circles.

4. If two circles touch each other at just one point, the circles are _______.

5. An arc that is exactly half the circle is called a _______.