Basic Math and Pre-Algebra
PART 3. The Shape of the World
CHAPTER 15. Circles
Segments and Angles
When an angle is drawn so that its vertex is at the center of a circle, it’s called a central angle. A central angle is an angle formed by two radii. The measure of a central angle is equal to the measure of the arc between the endpoints of its sides, its intercepted arc. The measure of a central angle is equal to the measure of its intercepted arc, and the measure of the arc is the measure of the central angle that cuts it off. The two measurements are interchangeable.
DEFINITION
A central angle is an angle with its vertex at the center of a circle whose sides are radii.
A chord is a line segment whose endpoints lie on the circle. The longer the chord, the closer it will be to the center of the circle. Short segments will fit near the edge, but longer ones will have to go closer to the center. The diameter is the longest chord of a circle. It passes through the center of the circle. The diameter is twice as long as the radius.
When you draw a chord, you divide the circle into two portions, two arcs, usually a major arc and a minor arc. You think of the minor arc as being the arc that belongs to that chord. If you draw two chords in the same circle and the two chords are the same length, then the arcs they cut off will be the same size. Congruent chords cut off congruent arcs.
DEFINITION
A chord is a line segment that connects two points on a circle. The diameter is the longest chord that can be drawn in a circle and passes through the center.
If you draw two radii, they both come from the center point, and they form a central angle. If you draw two chords that come from the same point on the circle, you form an angle that also intercepts an arc, but you can see that it’s smaller than the central angle that intercepts that same arc. An inscribed angle is an angle whose sides are chords and whose vertex lies on the circle. In the figure, central angle ∠AOB and inscribed angle ∠ACB both intercept arc ![]() but you can see that ∠ACB is smaller.
but you can see that ∠ACB is smaller.
DEFINITION
An inscribed angle is an angle with its vertex on the circle whose sides are chords.
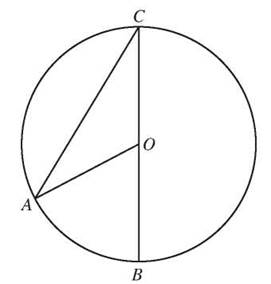
If you look at ∆AOC, you can see it’s an isosceles triangle because radii AO = OC, and that means that m∠OAC = m∠OCA. In addition, ∠AOB is an exterior angle of the triangle, so m∠AOB = m∠OAC + M∠OCA = 2m∠OCA. That means the central angle is twice the size of the inscribed angle, or, in other words, the inscribed angle is half the size of the central angle. The measure of an inscribed angle is equal to one-half the measure of its intercepted arc.
Suppose that in circle O, ![]() and
and ![]() are radii and
are radii and ![]() and
and ![]() are chords. If
are chords. If ![]() = 50°, find m∠AOB and m∠ACB.
= 50°, find m∠AOB and m∠ACB.
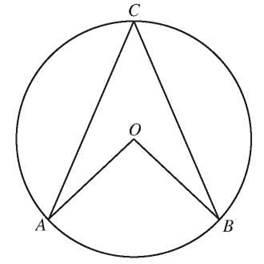
![]() is the intercepted arc for both angles. m∠AOB is a central angle, so its measure is the same as the measure of the arc. m∠AOB = 50°. m∠ACB is an inscribed angle, so its measure is half the measure of the arc m∠ACB = 25°.
is the intercepted arc for both angles. m∠AOB is a central angle, so its measure is the same as the measure of the arc. m∠AOB = 50°. m∠ACB is an inscribed angle, so its measure is half the measure of the arc m∠ACB = 25°.
WORLDLY WISDOM
An angle inscribed in a semicircle is a right angle.
When two chords intersect within a circle, they form four angles, which are labeled with numbers in the figure. Vertical angles are congruent, so ∠1 ≅ ∠3 and ∠2 ≅ ∠4. You might look at the picture and think that arc AC is smaller than arc BD (and you’d be right), and so you might wonder how the two angles could have the same measurement.
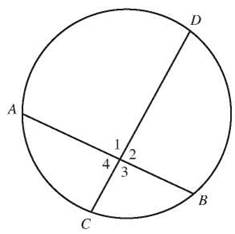
Draw chord AD to make a triangle. ∠4 is an exterior angle of that triangle, and so it’s equal to m∠DAB + m∠CDA. Those are inscribed angles, so ![]() But then you notice that ∠2 is also an exterior angle of that triangle and equal to exactly the same thing. The measure of an angle formed by two chords (and the measure of its vertical angle partner) is one-half the sum of the two intercepted arcs. To find the measure of an angle formed by two chords, average the arcs intercepted by the two vertical angles.
But then you notice that ∠2 is also an exterior angle of that triangle and equal to exactly the same thing. The measure of an angle formed by two chords (and the measure of its vertical angle partner) is one-half the sum of the two intercepted arcs. To find the measure of an angle formed by two chords, average the arcs intercepted by the two vertical angles.
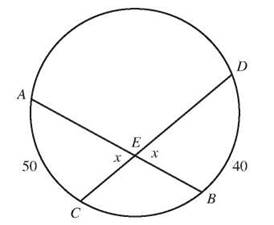
If two chords intersect in the circle as shown, and you want to find the value of x, you just need to realize that the two vertical angles whose measure is x intercept arcs of 40° and 50°. Then ![]()
CHECK POINT
6. ∠TOP is a central angle in circle O, and arc ![]() measures 48°. Find the measure of ∠TOP.
measures 48°. Find the measure of ∠TOP.
7. Points M, A, and N lie on circle O. Arc ![]() measures 78°. Find the measure of ∠MAN.
measures 78°. Find the measure of ∠MAN.
8. Diameter ![]() meets chord
meets chord ![]() at point I on circle P. Arc
at point I on circle P. Arc ![]() measures 36°. Find the measure of ∠SIT.
measures 36°. Find the measure of ∠SIT.
9. In circle P described in question 8, chords ![]() and
and ![]() meet each other at point T and meet the ends of diameter
meet each other at point T and meet the ends of diameter ![]() . Find the measure of ∠ITS.
. Find the measure of ∠ITS.
10. Chords ![]() and
and ![]() intersect at point A inside circle O. Arc
intersect at point A inside circle O. Arc ![]() measures 56° and arc
measures 56° and arc ![]() measures 82°. Find the measure of ∠GAL and the measure of ∠PAL.
measures 82°. Find the measure of ∠GAL and the measure of ∠PAL.