Basic Math and Pre-Algebra

PART 3. The Shape of the World

CHAPTER 15. Circles

Area and Circumference

When you explored polygons, whether triangles, quadrilaterals, or polygons with more sides, you always wanted to know two things: how to quickly find the distance around the edges of the polygon (its perimeter), and how to measure the area enclosed by the polygon. You want to be able to do these same things for the circle.

The circumference of a circle is the distance around the circle. The circumference is the circle’s equivalent of the perimeter of a polygon. The distance around a circle is a little more than three times the diameter of the circle. The formula for the circumference of a circle is C = πd, where d is the diameter of the circle and π (pi) is a constant approximately equal to 3.14159.

DEFINITION

The circumference of a circle is the distance around the circle. The word circumference comes from Latin. Circum is the preposition for around, and ferre is a verb that means carry. If you carry something around the circle, you trace out the circumference.

You sometimes see the formula as C = 2πr, because r is the radius of the circle, and the diameter is twice the radius. Because π is an irrational number, many times you’ll give your answer as a number times π, for example, 9π. If you use an approximate value, you’ll want to say “approximately equal” when you give your answer. For most questions, you can use 3.14 or 22/7 as approximate values of π.

Suppose the circumference of circle O is 40π cm. To find its radius, use the circumference formula C = πd = 40π. The diameter must be 40 cm, and therefore the radius is half of that, or 20 cm.

The area of a circle, the space enclosed by the circle, can be approximated in a number of ways. One is to sandwich it between a polygon whose sides are tangent to the circle, called a circumscribed polygon, and a polygon whose vertices are on the circle, called an inscribed polygon. The area of the circle will be larger than the area of the inscribed polygon but smaller than the area of the circumscribed polygon. To get a good approximation, however, you would have to use polygons with many sides and that makes for difficult calculations.

DEFINITION

A polygon is circumscribed about a circle if the polygon surrounds the circle with each side tangent to the circle. A polygon is inscribed in a circle if each of its vertices lies on the circle.

Here’s a way to approximate the area of the circle that’s a little easier. Cut the circle into wedges, like a pie. Line up the wedges, alternating point up and point down. It should look like this:

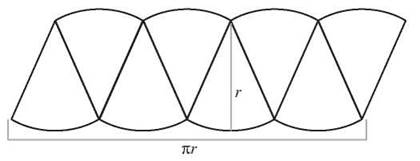
The rearranged area looks a lot like a parallelogram. The height of the parallelogram is the radius of the circle, and the base is half the circumference, or πr. The area is base times height, or r times πr, which equals πr². The area of a circle is the product of π and the square of the radius. To find the area of a circle whose radius is 7 inches, you could just square 7 to get 49 and say the area is 49π square inches. That’s absolutely true, but if you don’t really have a sense of what 49π means, you could use square inches.

CHECK POINT

16. Find the area of a circle with a radius of 9 cm.

17. Find the circumference of a circle with a diameter of 12 inches.

18. Find the area of a circle with a diameter of 32 cm.

19. Find the circumference of a circle with an area of 36π square meters.

20. Find the area of a circle with a circumference of 24π feet.