Basic Math and Pre-Algebra

PART 3. The Shape of the World

CHAPTER 16. Surface Area and Volume

Prisms

First up are polyhedrons, figures made from polygons that meet at their edges. The polygons are called faces of the polyhedron.

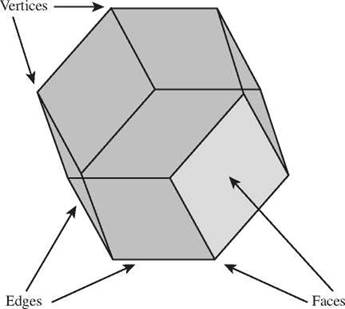
A polyhedron is a solid constructed from polygons that meet at their edges. Each of the polygons is a face of the polyhedron.

Polyhedrons come in two varieties: prisms and pyramids. A prism is a figure that has a pair of parallel bases, connected to one another by parallelograms. There’s enough math-speak in that sentence to scare even the bravest reader, so let’s take it apart and look at some examples. Look at the book you’re holding. It has rectangles for front and back covers, and those are parallel. The edges of the pages and the spine of the book form rectangles that connect the front cover to the back cover. When it’s closed, the book is a prism, specifically a rectangular prism.

A cube, like a die, is an example of a prism, and a rather special one because all its faces are squares. Many boxes are good examples. You might have even seen fancy boxes with tops and bottoms that have six or eight sides. Those are prisms, too, but they’re hexagonal prisms if the bases have six sides or octagonal prisms if the bases have eight sides. You may have seen a type of candy that’s packed in a triangular prism. The ends of the box are triangles, and the three sides that connect the triangles are rectangles.

DEFINITION

A prism is a polyhedron with two parallel faces connected by parallelograms. Prisms take their names from the polygons that form the bases, such as a rectangle or octagon. The exception is the cube, which is a prism whose faces are all squares.

Most of the examples you see around you are what mathematicians call right prisms. That means that the two bases are positioned in line with one another so the sides meet the bases at a right angle. It is possible to make a prism that isn’t right and seems to lean to one side, but you don’t see them being used very often.

DEFINITION

A prism is a right prism if the parallelograms meet the bases at right angles.

Surface Area

Questions about the surface area can be answered by finding the area of each face of the solid and adding them up. It’s often easier just to disassemble the prism, and then think about the area of the pieces. Do you have a triangular prism? That’s two triangles for the bases and three rectangles around the sides. Check for the dimensions of each and go to work on the areas.

MATH TRAP

Don't automatically assume that all the parallelograms are the same size. If your bases are regular polygons, it might be true, but make sure you check first.

Suppose you’re looking for the surface area of a triangular prism that stands 6 inches high, and the triangular bases are equilateral triangles with sides 3 inches long. You need to find the area of the two equilateral triangles and the area of the 3 rectangles.

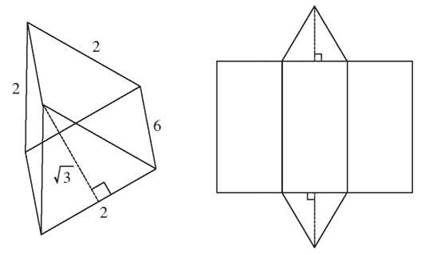
Each rectangle is 6 inches long and 2 inches wide, so each has an area of 12 square inches.

The equilateral triangles have a base of 2 inches, but you need a height, and for that you have to remember your 30-60-90 right triangles. The height of an equilateral triangle is half the length of a side times the square root of three, or in this case, 1√3. The area of each triangle is 

The total surface area is the two triangles plus the three rectangles or 2(√3) + 3(12) = 36 + 2√3 ≈ 39.46 square inches. The area of the three rectangles is called the lateral area.

DEFINITION

The lateral area of a prism is the total of the areas of the parallelograms surrounding the bases.

Coming up with a formula for that process is difficult because of all the different possibilities for the number of edges of the base and therefore the number of rectangles around it. Add the fact that the bases may or may not be regular polygons, and it’s amazing that you can get any kind of formula, but you can.

Imagine a prism 6 inches high whose bases are 3-4-5 right triangles. The surface area is  Let’s rewrite those last three pieces, so the surface area looks like this:  The sum in the parentheses, 3 + 4 + 5, is the perimeter of the base. So you can say the surface area of the prism is two times the area of the base plus the height (h) times the perimeter of the base. If you use B for the area of the base and P for the perimeter of the base, the formula is SA = 2B + hP.

The surface area of a rectangular solid, is SA = 2LW + 2Lh + 2Wh = 2LW + h(2L + 2W) = 2(area of base) + h(perimeter of base). Let’s apply this to the rectangular prism shown.

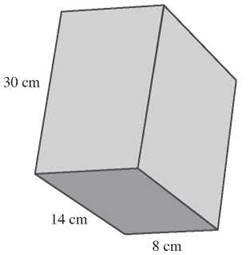
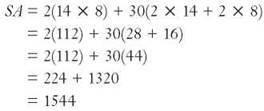
The surface area is 1,544 square centimeters.

CHECK POINT

Find the surface area of each prism. SA = 2B + hP

1. A rectangular prism with edges of 15 cm, 24 cm, and 10 cm.

2. A triangular prism 8 inches high, with a base that is a right triangle with legs 5 inches and 12 inches long and a hypotenuse 13 inches long.

3. A hexagonal prism 42 cm high with a base that is a regular hexagon with a perimeter of 30 cm and an area of 65 square cm.

4. A pentagonal prism, 4 inches high, with a base that is a regular pentagon with sides 15 inches long and an area of 387 square inches.

5. A cube 17 cm on each edge.

Volume

Rather than memorizing a lot of different volume formulas, remember that the volume of a prism is equal to the area of its base times its height. If you use B for the area of the base, V = Bh.

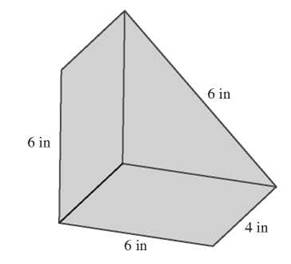
If you need to find the volume of a triangular prism 4 inches high, whose base is an equilateral triangle with sides 6 inches long, first you’ll need to find the area of the base. Because it is an equilateral triangle, you can use the 30°-60°-90° triangle relationship to find the height. The altitude of the equilateral triangle is half the side times the square root of three, or 3√3. The area of the triangle is  square inches. Finally, the volume of the prism is the area of the base times the height, or 9√3∙4 = 36√3 cubic inches.

WORLDLY WISDOM

Volume is always measured in cubic units.

To find the volume of a rectangular prism with length of 15 inches, width of 9 inches, and height of 14 inches, first find the area of the base, 15 x 9 = 135 square inches, and multiply the area of the base by the height. 135 x 14 = 1890, so the volume of the rectangular prism is 1,890 cubic inches.

The volume of a rectangular prism is still V = Bh, but because the area of B is length times width, the volume of a rectangular prism is sometimes written as V = lwh.

CHECK POINT

Find the volume of each prism. V = Bh

6. A cube 7 inches on each edge.

7. A rectangular prism with edges of 12 cm, 21 cm, and 15 cm.

8. A triangular prism 6 inches high, with a base that is a right triangle with legs 3 inches and 4 inches long and a hypotenuse 5 inches long.

9. A pentagonal prism, 8 inches high, with a base that is a regular pentagon with sides 15 inches long and an area of 387 square inches.

10. A hexagonal prism 50 cm high with a base that is a regular hexagon with a perimeter of 30 cm and an area of 65 square cm.