Basic Math and Pre-Algebra
PART 3. The Shape of the World
CHAPTER 16. Surface Area and Volume
Cones
If cylinders behave a lot like prisms, it’s not surprising that cones have a lot in common with pyramids. Like cylinders, cones have a circle as their base. Like pyramids, their lateral surface slopes to a point. Trying to unroll a cone is a bit trickier than taking the label off a can, as you did with the lateral area of a cylinder. If you try to unroll the cone’s lateral area, you’ll find it’s part of a circle, but how big a part depends on the size of the base circle.
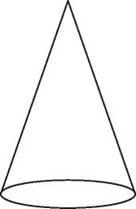
A cone is a solid with a circular base and a lateral surface that slopes to a point.
Surface Area
The surface area of a pyramid is equal to the area of the base plus the combined area of all the surrounding triangles. That lateral area, you learned, was equal to 1/2 x perimeter x slant height. For a cone, the surface area is still the area of the base plus the lateral area. The base is a circle, so the area of the base is πr2. If the slant height is l, the lateral area is a fraction of the area of a circle with area πl2. What fraction? The fraction you create when you put the circumference of the base, 2πr, over the circumference of a circle with radius equal to the slant height. ![]() The lateral area is πrl, so the surface area is SA = πr2 + πrl.
The lateral area is πrl, so the surface area is SA = πr2 + πrl.
To find the surface area of a cone with a radius of 8 cm and a slant height of 10 cm, find the area of the base. πr2 = π(82) = 64π, and then calculate πrl = π(8)(10) = 80π. The surface area is 64π + 80π = 144π square centimeters.
Volume
The volume of a pyramid is one-third of the volume of a prism with the same base and height. Conveniently, the volume of a cone is one-third of the volume of a cylinder with the same base and height. For a cone, ![]()
To find the volume of a cone 9 meters high with a base that has a radius of 8 meters, follow the formula.
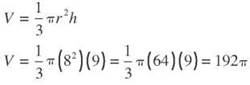
The volume is 192^ cubic meters, or approximately 603.2 cubic meters.
CHECK POINT
Find the surface area and volume of each cone. SA = πr2 + πrl and ![]()
26. A cone with radius 10 cm, height 24 cm, and slant height 26 cm.
27. A cone with diameter 8 inches, height 3 inches, and slant height 5 inches.
28. A cone with circumference 16π cm, height 6 cm, and slant height 10 cm.
29. A cone with radius 12 inches and height 5 inches. (Hint: Use the Pythagorean theorem to find the slant height.)
30. A cone with base area 324π cm and a height of 24 cm.