Basic Math and Pre-Algebra
PART 3. The Shape of the World
CHAPTER 17. Geometry at Work
Areas of Irregular Figures
Once you know how to find the area of a certain type of polygon, it becomes a routine process. From time to time, you may have to work backward, if you’re given the area and need to find one of the dimensions, but that’s not all that difficult. The interesting problems are the ones that combine those basic formulas with a little bit of cut-and-paste thinking to figure out how to find the area of that!
It may be a figure that doesn’t fit any rule when you take it as a whole, but can be broken down into sections that fit common rules nicely. For those problems, the trick is to break the figure up in a way that leaves you with figures whose areas you know how to find and whose dimensions you know or can find easily. Your strategy is to break the figure into parts, find their areas, and then put it all back together.
The other type of problem is one in which the overall outline of the shape does fit a rule but it has holes cut out of it. In those cases, the best tactic is to find the area of the whole shape and then subtract the area of the holes. “Whole minus holes” if you want a shortcut.
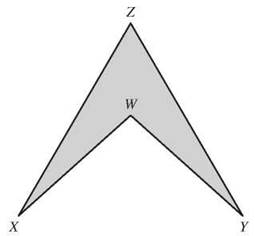
Let’s take a look at one of these more interesting problems. The figure shown here is a quadrilateral, but it’s definitely not part of the family of parallelograms. It’s called a concave polygon. That dent from X to W to Y is where it caves in. Concave polygons cave in. Officially, a polygon is concave if one of its diagonals falls outside the polygon. If you tried to draw a diagonal from X to Y, it would be outside the quadrilateral.
DEFINITION
A concave polygon is one in which one or more diagonals falls outside the polygon. A convex polygon is one in which all the diagonals fall inside the polygon.
All that is nice, but how do you find the area of something like that? You could divide and conquer. Draw ZW and divide the figure into two triangles. Find the area of each and add them together.
Of course, to find the area of each triangle, you need to know the lengths of a base and the height to that base. If you knew that ZW = 4 cm and that an altitude from X to the extension of ZW measures 3 cm, you could calculate the area of ∆XWZ as 1/2 x 4 x 3 = 6 square centimeters. If the altitude from Y is also 3 cm, you have the polygon broken into two triangles, and each triangle has an area of 6 square centimeters, so the quadrilateral has an area of 12 square centimeters.
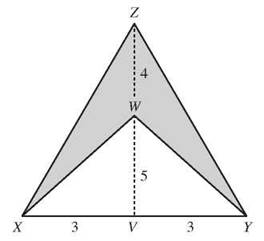
Or you could add more lines to the figure. Connect X and Y, draw 
and extend it to meet 
at V. Find the area of ∆XZY and the area of ∆XWY and subtract. If XV and YV are both 3 cm, XY is 6 cm. ZW is 4 cm, and if WV is 5 cm, you can calculate the area of ∆XZY as 1/2 x 6 x 9 = 27 square centimeters, and the area of ∆XWY = 1/2 x 6 x 5 = 15 square centimeters. Subtracting 27 - 15 gives you the area of the quadrilaterals as 12 square centimeters.
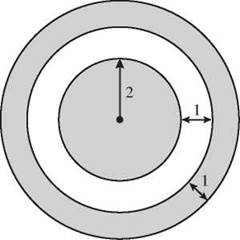
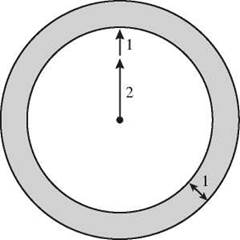
It’s not uncommon to be asked to find the area of part of a figure, the portion shaded in this picture. In problems like these, it can be confusing to find the measurements you actually need. In this target diagram, the two outer rings are marked as 1 inch wide, but there’s no convenient formula for the area of a ring.
MATH TRAP
When you're looking for the area of a shaded region, be careful to take the shape apart carefully. It's easy to include area you don't really want or miss area you do want if you rush to get an answer.
To find the shaded area, you’re going to have to devise a way to get the area of that outer ring. You can deal with the circle in the middle later. It’s a circle. You know what to do with that. Try thinking about the picture as a big gray circle with a smaller white circle sitting on top.
WORLDLY WISDOM
Taking the time to sketch out the portions of the figure before you begin calculating is time well spent. Especially if you're thinking of the figure as shaded and unshaded layers, it's wise to sketch the layers separately.
The smaller white circle has a radius of 3 inches. The gray circle underneath is an inch bigger, so its radius is 4 inches. The area of the big gray circle is 42 times pi, or 16π square inches. The white circle has an area of 32 times pi, or 9π square inches. The part of the gray circle peeking out from behind the white circle, the gray ring, has an area of 16π - 9π = 7π square inches.
Now that you know the area of that outer ring, you can bring back the gray circle in the middle. It has a radius of 2 inches, so its area is 4π square inches. Add that to the outer ring, and you have a shaded area of 7π + 4π = 11π square inches.
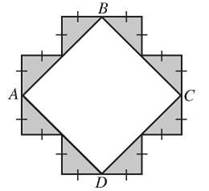
You’ve looked at circles in circles, what about squares in squares? In this figure, the area of square ABCD is 32 square centimeters. To find the area of the shaded region, work backward to find the dimensions you need. Square ABCD has an area of 32 square centimeters, so each of its sides is √32 = √16√2 = 4√2 centimeters. What you need, however, is to find the area of the gray isosceles triangles.
Each side of the square fits the hypotenuses of two triangles, so each hypotenuse is half of 4√2, or √2 centimeters. In an isosceles right triangle, with two legs the same length, the Pythagorean theorem says a2 + b2 = a2 + a2 = 2a2 = (2√2)2. That means that 2a2 = 8, a2 = 4 and a = 2, so each leg of the little gray triangles is 2 centimeters long. The area of each little triangle is 1/2 x 2 x 2 or 2 square centimeters, and there are 8 triangles, making the total shaded area 16 square centimeters.
WORLDLY WISDOM
Leave any square roots in radical form at least until the end of your calculation. If you move to a decimal approximation sooner, you'll have to do your arithmetic with that decimal. That's more work, plus it's approximate to begin with, and you may need to round more at the end. Wait, keep the radical, and then, if you really need a decimal approximation, do it when all the calculation is done.
CHECK POINT
Find the shaded area in each figure.
