Basic Math and Pre-Algebra

PART 3. The Shape of the World

CHAPTER 17. Geometry at Work

Similarity and Congruence

When we talk about how polygons relate to one another, we most often talk about congruence and similarity. Two polygons are congruent if they are the same shape and the same size. They’re copies of one another, as if you ran one through a copier. Two polygons are similar if they’re the same shape but different sizes. Think about enlarging a photo without distorting the image. Polygons of any number of sides can be congruent or similar, but most often you will encounter congruent triangles or similar triangles.

Congruent Triangles

Triangles are congruent if they are the same shape and the same size. Because the size of the angles controls the shape of the triangle, in a pair of congruent triangles, you can match up angles that are the same size. In other words, corresponding angles are congruent. Because the length of sides controls size, corresponding sides are of equal length, or congruent.

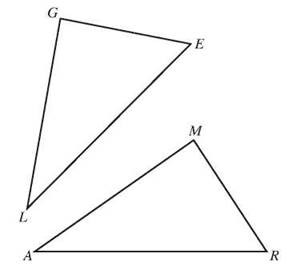
Two triangles are congruent if each pair of corresponding sides are congruent and each pair of corresponding angles are congruent.

If ∆ARM ≅ ∆LEG, ∠A and ∠L will be the same size, ∠R will have the same measurement as ∠E, and m∠M = m∠G. Sides are congruent as well. and

The order in which the vertices of the triangle are named tells you what matches. You can sometimes tell what matches by looking at a picture, but unless you’re told the measurements, or you can actually measure, you can’t always be certain. The order in which the vertices of the triangles are named will tell the correct match-up.

Of course, that assumes that someone told you that the triangles were congruent. What if they asked you if the triangles were congruent? Technically, you’d have to measure all the sides and all the angles of both triangles and check to see that you can match up parts of the first triangle with parts of the second so that corresponding parts are congruent. That’s what the definition of congruent triangles says.

That’s a lot of measuring, and you might realize that, for example, you don’t really have to measure the third angle of each triangle. If you measure the first two angles of both triangles and they match, the third angles will have to match as well, because the three angles of any triangle always add to 180°. That might get you to thinking about whether there’s anything else you can skip.

It turns out that to be certain that two triangles are congruent, you only need to check three measurements from each triangle. You must always have at least one pair of congruent sides, to guarantee that the triangles are the same size. If you only have the measurements of one side of each triangle, and they are congruent, then you must have two pairs of matching angles to be certain the triangles are congruent. It can be any two pairs, because if you know that two pairs of angles are congruent, the third pair will match as well. If you measure two pairs of sides and find that they match, and you can show that the angles they form also match, you can be certain the triangles are congruent.

If you were to cut three sticks to set lengths and tried to put them together into triangles, you’d find out there’s only one triangle you can make. If you measure all three pairs of sides in two triangles and they match, you don’t need to measure any angles before you decide the triangles are congruent. Three pairs of congruent sides congruent is enough.

Each of these “minimum requirements” involves three pieces, and each one has a three-letter abbreviation.

Minimums Required To Be Certain Triangles Are Congruent

CHECK POINT

Decide if the information given is enough to guarantee that the triangles are congruent. If so, state the rule that guarantees the congruence. If not, write “cannot be determined.”

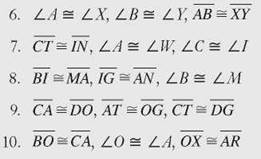
Similar Triangles

Triangles are similar if they are the same shape, but not necessarily the same size. Because they have to be the same shape, and angles control shape, corresponding angles are congruent. They don’t have to be the same size, so you don’t have to have corresponding sides congruent, but to change the size without distorting the triangle, corresponding sides will be in proportion. If the longest side of one triangle is twice the size of the longest side of the other triangle, then the shortest side of the first triangle will be twice the size of the shortest side of the second triangle. All the sides will be multiplied by the same number, called the scale factor.

DEFINITION

Two triangles are similar if each pair of corresponding angles are congruent and corresponding sides are in proportion.

The scale factor of two similar triangles is the ratio of a pair of corresponding sides.

To conclude that triangles are similar, you must know that all three pairs of corresponding angles are congruent, and you must check that sides are in proportion. Just like with congruent triangles, however, there are shortcuts. The most common one for similar triangles is called AA. You must know that two angles of one triangle are congruent to the corresponding angles of the other. Of course, if two pairs of angles are congruent, the third pair will be congruent, too. The second shortcut is to check that two pairs of sides are in proportion and the angles between them are congruent to each other. The third is to check that all the sides are in proportion. In fact, AA is the one used most often.

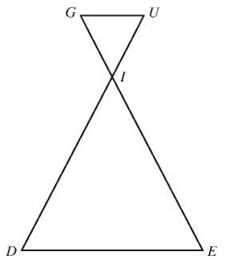
∆GUI will be similar to ∆EDI if ∠G ≅ ∠E and ∠U ≅ ∠D. The third angles are the pair of vertical angles, and vertical angles are congruent, so you know m∠GIU = m∠EID. The corresponding sides will be in proportion, When you know that two triangles are similar, you can use a little squiggly line to show their relationship, like this: ∆GUI ~ ∆EDI.

CHECK POINT

Write the proportion for each pair of similar triangles.

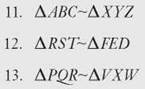
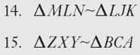
Finding Missing Measurements

The primary reason that you want to know if a pair of triangles might be similar or congruent is that it will help you find a measurement you need but can’t measure directly. If you know two triangles are congruent, you know you have two identical sets of measurements. Suppose ∆RST ≅ ∆MNP. If RS = 12 feet and ST = 18 feet, you can find the length of , even though it’s in the other triangle. Because corresponding parts of congruent triangles are congruent, MN = RS = 12 feet.

If you know triangles are similar, you know angles are congruent and sides are in proportion. Suppose ∆RST ~ ∆ABC, RS = 12 feet, BC = 6 feet and ST = 18 feet, and you need to find the length of . Use the fact that in similar triangles, corresponding sides are in proportion: . Fill in the known lengths. Cross-multiply and solve. 18x = 72, and x = 4. The length of is 4 feet.