Basic Math and Pre-Algebra
PART 3. The Shape of the World
CHAPTER 17. Geometry at Work
Indirect Measurement with Similar Triangles
Right triangles are often helpful in finding areas of irregular figures and in finding measurements indirectly, as you’ll see a little later. Triangles of many different shapes can be used for indirect measurement, if you use what you know about similarity.
Remember the two triangle relationships, congruence and similarity? Either one can help you find a measurement you can’t take directly, but in cases where you can’t measure directly, you may not be able to create an exact copy to use congruent figures. Similarity is easier because you can make a smaller copy of the same shape and then use similar triangles to find the measurement of the larger version.
Similar polygons are the same shape but not necessarily the same size. Because their sides are in proportion, however, you can use a smaller version of the figure to calculate the measurements of a larger one.
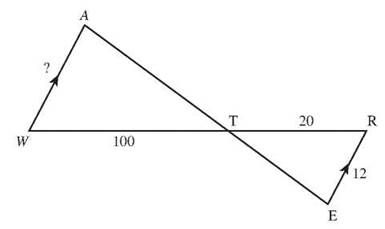
If you need to know how wide the river is from point W on one bank to point A on the other bank, you can’t walk on water to take the measurement. But you can measure off 100 meters along one bank and mark point T, then go another 20 meters and mark point R. Create ∆RET to be similar to ∆WAT by making side RE parallel to side WA, and ∠WTA = ∠RTE. (Okay, you probably don’t walk around with a protractor in your pocket, but it’s possible to do it.) Measure RE and set up the proportion ![]() You can plug in what you know, and solve for WA.
You can plug in what you know, and solve for WA.
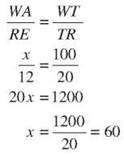
The river measures 60 meters from W to A.
If you want to know if that big tree in your local park is as tall as the holiday tree in Rockefeller Center, you’re not going to climb the tree with a yardstick. But you can go down to the park with a friend on a sunny day and use the sun, your friend, and similar triangles to help you measure the tree.
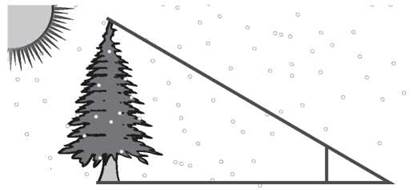
The sun will cause the tree to throw a shadow on the ground, and although you can’t easily measure the tree, you can measure its shadow. Have your friend stand up nice and tall beside the tree and measure his height and the length of his shadow. The tree and its shadow form the legs of a right triangle (with a ray of sunlight as its hypotenuse). Your friend and his shadow make the legs of a similar right triangle. You can set up a proportion to find the height of the tree.
If your friend is 5 feet tall and casts a shadow 2 feet long, and the tree’s shadow is 30 feet long, your proportion will look like this.

Your tree is 75 feet tall, just a foot shorter than the 2013 Rockefeller Center tree.
CHECK POINT
Find the length of the specified segment.
16. ∆GHI~∆ARM, GH = 9 ft, GI = 8 ft, AR = 12 ft. Find AM.
17. ∆JKL~∆DOG, JK = 17 m, JL = 25 m, DG = 30 m. Find DO.
18. ∆ABC~∆XYZ, AB = 21 cm, BC = 54 cm, XY = 7 cm. Find YZ.
19. ∆DEF~∆CAT, DE = 65 in, EF = 45 in, CA = 13 in. Find AT.
20. ∆MNO~∆LEG, MN = x - 3, NO = 3, EG = 21, LE = 2x + 4. Find LE.