Basic Math and Pre-Algebra

PART 4. The State of the World

Your great adventure in the world of numbers is almost over, at least for now. Hopefully, you’ve enjoyed enough of this tour to want to visit at least some of these areas again.

What’s left on the agenda? Well, when you’ve had a great adventure, you usually want to report on your experience when you get home. Telling people about what you’ve seen and what you’ve learned often means using some statistics, like the average rainfall in Thailand or the number of people who ride the Tube every day in London. Statistics are numbers that summarize a larger collection of information, and the heading “Statistics” also includes charts and graphs and other means of communicating the “big picture.” This last part of your journey is about assessing risks and possibilities—probability—and summarizing what you’ve found out—statistics. These will help you make smart decisions and share what you’ve learned with the folks back home. Include a few photos—or charts and graphs—to keep things interesting for them.

CHAPTER 18. Probability

Math is all about the one right answer, right? Not so fast. It would be comfortable if everything had an absolutely certain right answer, but that’s often not the case. One of the greatest skills math gives us is the ability to talk about possibility and uncertainty in an organized way. When you can’t be certain that something is going to happen, being able to talk the chance of it happening and being able to assign a number to that chance is helpful.

In this chapter, you’ll explore ways to assign a number to the likelihood that something will happen. You’ll do that by comparing to all the things that could happen. In simple situations, that’s all you need to do, but you’ll see there are some rules to make the more complicated situations easier to handle. For all of this, you’ll have to do a lot of counting, so let’s start with a look at efficient methods of counting.

Counting Methods

You know how to count, of course. If you had a bag of marbles, some red and some blue, and you wanted to know the chance that the first marble you pulled out (without looking) was a blue marble, the first thing you’d want to know is how many red marbles and how many blue marbles are in the bag. Unless it was a gigantic bag of marbles, you could answer that question by counting.

On the other hand, suppose you were going to buy a lottery ticket that asked you to pick five numbers from a group of 50, and you had to get all five correct to win. Your chance of winning will depend on how many ways there are to pick five numbers, and that counting problem is more complicated.

When you start to pick your number for the lottery ticket, you have 50 numbers to choose from. After you pick your first number, there are 49 left to choose from for the second number, then 48 for the third, 47 for the fourth, and 46 for the fifth. (That’s assuming you have to pick five different numbers. If you’re allowed to repeat, you have 50 choices each time.) And there’s another question, too. Do you have to have the five numbers in just the right order? Is 12345 the same as 54321? Or are those different?

Big counting jobs raise many questions, but there are some rules that will help. Let’s start with the most essential rule.

Basic Counting Principle

The fundamental rule for quick counting is called the basic counting principle. It gives you a fast way of counting up the possibilities by multiplying the number of choices. Suppose you’re getting dressed and you need to choose jeans or khakis and then pick a shirt from the six t-shirts in the drawer. You could wear any one of the six t-shirts with jeans, or any one of the six t-shirts with khakis. That’s 12 possible outfits: 2 choices for pants times 6 choices for shirts.

If you have to do something that requires several choices, and you create a slot for each choice that needs to be made and fill each slot with the number of options for each choice, multiplying those numbers will tell you how many different possibilities you have.

If you have 5 shirts, 4 pairs of slacks, and 3 pairs of shoes, and you’re comfortable mixing and matching any of them, how many different outfits can you make? Using the basic counting principle, create a slot for shirts, a slot for slacks, and a slot for shoes:

Then fill in the number of each that you have and multiply.

Now, if you’re willing to do laundry often so everything is wearable, you could wear a different outfit every day for almost two months with just those few items. Add a couple of sweaters, and you’d be set for almost four months.

So what about that lottery ticket? Let’s suppose you can’t repeat numbers, but you do have to have them in the right order. The basic counting principle says you can multiply the number of options you have for each choice to find the total number of ways to pick five numbers from the pool of fifty.

That’s over 250 million different ways to pick five numbers, and only one will win.

CHECK POINT

Your favorite salad bar has 2 kinds of greens, 5 different veggie toppings, 3 crunchy toppings, and 4 dressings. How many different salads can you make if you choose...

1. Greens and a dressing?

2. Greens, a veggie, and a dressing?

3. Greens, a veggie, a crunchy topping, and a dressing?

4. Greens, 2 different veggies, and a dressing?

5. Greens, 2 different veggies, 2 crunchy toppings, and a dressing?

Permutations

A popular television game show has a game in which the contestant is told all the digits in the price of the very expensive prize (usually a car or a trip), but the contestant only wins the prize if he or she can put the digits in the correct order. Depending on how many digits there are, the chance of guessing correctly may be pretty good or pretty terrible.

If I told you that the digits in the price of your prize are 3 and 6, you’re either going to guess 36 or 63. There are only two possible answers, and one of them is right. Basic counting principle says 2 choices for the first digit times 1 choice for the second digit gives you two possibilities. But you’re not going to find a car for $36 or for $63. There will be quite a few digits in the price of the car or trip or other expensive prize. How many possibilities would there be if you had to put 5 digits in order? Or 6 digits?

This question of the number of ways you can arrange a group of things—numbers, letters, people, whatever—is the question of how many permutations there are. The word permutation means arrangement or ordering.

DEFINITION

A permutation is an arrangement or ordering of a group of objects.

You can answer the question about the number of permutations by using the basic counting principle. If you have to put five digits in order, there are 5 x 4 x 3 x 2 x 1 = 120 permutations. This pattern of multiplication, from a number (in this case, 5) down to 1, is called a factorial. The symbol for factorial is an exclamation point. 5! = 5 x 4 x 3 x 2 x 1 = 120.

The number of orders in which the 8 children on a soccer team could line up at the water fountain, or the number of different arrangements of 8 people taken 8 at a time, is 8! = 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1 = 40,320. For any number n, the permutations of n things taken n at a time is n!

But what if you’re not taking n things at a time? For example, a baseball team needs to put 9 players on the field but might have 25 players on the roster. Now, if you know anything about baseball, you know that the players aren’t all interchangeable, but still, how many permutations of 25 people taken 9 at a time are possible?

Your best strategy is to go back to the basic counting principle. Make nine slots and start filling them from 25 on down. 25 x 24 x 23 x 22 x 21 x 20 x 19 x 18 x 17. Multiply that out and you get ≈ 7.4 x 1011. That’s approximately 740 billion possible lineups. Maybe it’s a good thing the players aren’t all interchangeable.

You’re still talking about an arrangement, or permutation, but an arrangement of 9 out of the 25, not all 25. You don’t want the entire 25!, but you do want the first 9 slots of it. You can write a formula for the permutations of n things taken t at a time as

In this case, the permutations of 25 things taken 9 at a time is 25!

Do you see how the factorial in the denominator cancels the part of the factorial in the numerator that you don’t want? And isn’t it good to know you don’t have to write out all those factorials all the time?

So if you need the permutations of 7 things taken 4 at a time, the basic counting principle says you want 7x6x5x4, and the permutation formula says . The approaches are different, but the result is the same.

CHECK POINT

6. What is 6!?

7. What is 7!?

8. What is 7! ÷ 6?

9. Find the permutations of 9 things taken 3 at a time.

10. Find the permutations of 10 things taken 4 at a time.

Combinations

If 8 people are candidates in a school board election and the top two finishers will serve on the board, you might ask how many permutations of 8 people taken two at a time are possible. You can calculate that  There are 56 different orders of finish.

On the other hand, if both of the top two finishers will serve, regardless of which is first and which is second, the order in which they finish doesn’t really matter. Mr. Smith and Ms. Jones is a different permutation from Ms. Jones and Mr. Smith, but they both give you the same school board members.

Because all the different arrangements of the same two people shouldn’t count separately, the number of permutations is too big, but it can give you a place to start. There are 56 permutations, or arrangements, of 8 people taken 2 at a time, but fewer combinations or groups in which order doesn’t matter. Specifically, there are half as many combinations as permutations.

DEFINITION

A combination is a way of selecting a number of objects from a larger group when the order of the objects is not significant.

What if the top three vote-getters were chosen for the school board, instead of the top two? There would be 8 x 7 x 6 = 336 permutations of eight people taken three at a time, but how many combinations? If you were to list all the permutations, your list would include some permutations that include Mr. Smith, Ms. Jones, and Dr. Johnson. How many permutations on the list include these three people? That’s the same as asking how many permutations are there of three people taken three at a time, and the answer is 3 x 2 x 1 = 6. Each group of three people contributes 6 permutations to the total of 336. Because there are six arrangements of these same three people—six arrangements of any three people—the number of permutations is six times larger than the number of groups or combinations. Dividing the number of permutations by 6, or  will give you the number of combinations. The combinations of n things taken t at a time is 

The permutations of 10 things taken 5 at a time is 

The combinations of 10 things taken 5 at a time is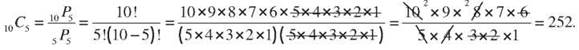 

The number of combinations will always be smaller than the number of permutations. Use permutations when the arrangement or order is important and combinations when a group should only be counted once, no matter how it’s arranged.

CHECK POINT

11. Find the number of combinations of 6 things taken 3 at a time.

12. Find the number of combinations of 7 things taken 4 at a time.

13. Find the number of combinations of 5 things taken 2 at a time.

14. How many different committees of 5 people can be chosen from a group of 12 people?

15. How many different ways can you order your ice cream sundae if you are going to choose 3 toppings from a list of 12 possibilities and the order in which you put toppings on does not matter?