Basic Math and Pre-Algebra

PART 4. The State of the World

CHAPTER 18. Probability

Probability of Compound Events

Basic probability is pretty simple. The number of ways things can go right, over the number of ways things can happen. But life is complicated. Things don’t always happen one at a time. In fact, they rarely happen one at a time. Usually there are at least two things to think about, but if you can handle them two at a time you can work your way through everything. It’s all about whether you want one or the other, or you want both.

Probabilities with “And”

Calculating the probability of a single card drawn at random from a standard deck being a 7 is fairly simple. There are four 7s out of 52 cards, so the probability is 4/52 or 1/13. Calculating the probability of a particular poker hand is much more complicated, because more cards are involved, and both the number of successes and the number of cards in the deck change as the deal goes on. That calculation begins, however, with finding the probability that you get two cards, two particular cards, one after the other. Let’s say you want a heart and then a diamond.

That’s drawing two cards, of course, not one. So how many ways are there to draw two cards from a deck of 52? That’s the permutations of 52 things taken 2 at a time, or 52 x 51 = 2,652. And how many ways to get a heart and then a diamond? Go back to your basic counting principle. There are 13 ways to get a heart on the first draw, and there are 13 ways to get a diamond on the second draw. 13 x 13 = 169 ways to get a heart and then a diamond. The probability of a heart and then a diamond is 169 out of 2,652. Let’s reduce that fraction.

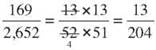
Another way to think about this is that the probability you get a heart on the first draw is 13/52, and the probability of a diamond on the second draw is 13/51. (The denominator is only 51 because you’ve already taken one card out of the deck.) 

Any time you need to find the probability of this event and that one, you want to multiply the probability of the first event by the probability of the second event. Suppose you roll a die, record the number that comes up, then roll again and record the second result. What’s the probability that both of them are even numbers? There are six possibilities for how the die can land, and three of them are even. The probability of two even numbers is 

Sometimes, when you look at the probability of two events occurring in sequence, the results of the first event have an effect on the probability of the second and sometimes it doesn’t. When you roll the die twice, the first roll doesn’t affect the second. They’re what we call independent events. The result of the first roll has no effect on the probabilities for the second.

When you drew the two cards, on the second draw, there would only be 51 cards to choose from, and that changes the probability. Drawing two cards without replacement is an example of dependent events, because the result of the first draw changes the probability for the second draw. But if you choose one card at random from a deck, record what it is, then put it back in the deck and shuffle before you pull a second card, the probabilities for the second draw are the same as the first.

If two cards are drawn at random from a standard deck, with replacement—that is, the first card is drawn, recorded, and replaced before the second card is drawn—the probability of drawing two aces is  If two cards are drawn without replacement, however, the probability of drawing two aces is 

CHECK POINT

A card is drawn from a standard deck, recorded, and replaced in the deck. The deck is shuffled, and a second card is drawn.

16. Find the probability of drawing a heart and then a queen.

17. Find the probability of drawing a heart and then a heart.

18. Find the probability of drawing a black card and then a red     card. Two cards are drawn at random from a standard deck, without replacing the first card.

19. Find the probability of drawing a king and a queen.

20. Find the probability of drawing two black cards.

Probabilities with “Or”

When you look at the probability of event A and event B happening, you multiply the probability of A times the probability of B. Multiplying these two fractions, both less than one, gives a smaller number. A smaller probability makes sense because it’s harder to have a success when success means having two different things happen than if success means having only one thing happen.

What if you want to find the probability of getting a five or a six when you roll a die? If you’re willing to accept either number as a success, your chance of success increases—in this case, it doubles. The probability of rolling a five or a six is the probability of rolling a five plus the probability of rolling a six. 

If you draw a card at random from a standard deck, what’s the probability of drawing a queen or a 10? The probability of drawing a queen is  and the probability of drawing a 10 is also  so the probability of drawing a queen or a 10 is 

Here’s a question that sounds the same, but be very careful. Don’t jump in without thinking it through. If you draw a card from a standard deck, what’s the probability of drawing an ace or a black card? Start with the probability of drawing an ace.  Then you want the probability of drawing a black card:  Before you add, think for a minute. There’s a little problem, or more accurately, two little problems: the ace of spades and the ace of clubs. The probability of an ace was based on four aces, including the ace of spades and the ace of clubs. The probability of a black card was based on 26 black cards, including the ace of spades and the ace of clubs. The two black aces are being counted twice, so you’ll have to make an adjustment for that.

In general, the probability of A or B is the probability of A plus the probability of B minus the probability of A and B.

You may wonder why this little adjustment wasn’t necessary in the example about rolling the die. The answer is that when you roll a die, getting a five and getting a six are mutually exclusive outcomes. There is no way that you can get a five and a six on the same roll. When event A and event B are mutually exclusive, the probability of A and B is zero, so  just becomes 

CHECK POINT

A bag contains 24 marbles. Six of the marbles in the bag are red, 4 are blue, 3 are white, 9 are green and 2 are yellow. One marble will be chosen at random.

21. What is the probability that the marble chosen is red or blue?

22. What is the probability that the chosen marble is yellow or blue?

23. What is the probability that the marble is green or white?

24. What is the probability that the chosen marble is yellow or red?

25. What is the probability that the marble is red or orange?

The Least You Need to Know

• To count quickly, take the number of options for each decision and multiply.

• The probability of an event is the number of ways it can happen over the total number of things that can happen.

• The probability of A and B is the probability of A times the probability of B.

• The probability of A or B is the probability of A plus the probability of B minus the probability of both.