Basic Math and Pre-Algebra
PART 5. Extra Practice
CHAPTER 21. Extra Practice
Part III: Geometry
Use the diagram to identify each of the following.
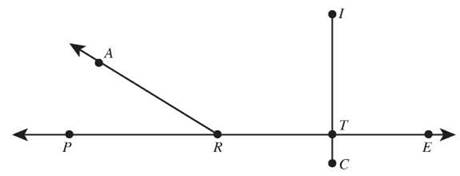
61. A ray
62. A line segment
63. An acute angle
64. An obtuse angle
65. A pair of vertical angles
Use the diagram to answer questions 66-70. 
and 
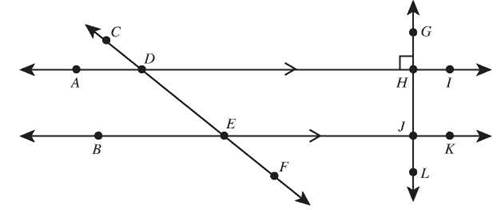
66. Name the angle that corresponds to ∠HDE.
67. ∠CDH and ∠BEF are a pair of _________ angles.
68. If m∠ADC = 20°, find m∠DEJ.
69. Find the measure of ∠HJK.
70. If m∠DEJ = 150°, find the measure of ∠HDE.
Find the missing measurements.
71. In ∆JAM, JA = AM. If m∠J = 80°, find m∠A.
72. If AR = 7 cm, RM = 13 cm, and ∆ARM is isosceles, then AM = _____ cm or _____ cm.
73. ∆LEG is a scalene triangle. LE = 4 cm and EG = 17 cm. The length of 
must be at least _____ cm but not more than _____ cm.
74. In ∆MAT, MA = 4 inches, AT = 4 inches, and MT = 6 inches. Is ∆MAT a right triangle?
75. ∆COW is a right triangle with right angle ∠O. If CW = 65 cm, and CO = 25 cm, find the length of 
.
76. If ∆PAT ≅ ∆POT and m∠A = 70°, then m∠O = _____.
77. ∆DOG ≅ ∆CAT, and DO = 28 in., OG = 34 in., and DG = 45 in. How long is CT?
78. ∆HOG ~ ∆PIG, and ∠OGH and ∠IGP are vertical angles. If HO = 14 cm, PI = 21 cm, and HG = 18 cm, find PG.
79. ∆RUG ~ ∆LAP, and RU is 8 centimeters longer than LA. If RG = 14 cm and LP = 10 cm, find RU.
80. ∆PLA is a scalene triangle, and side 
is extended through A to point Y and beyond, to form exterior angle APAY. If m∠PAY = 115° and m∠L = 75°, find m∠P.
Using the diagram, complete each sentence with parallelogram, rectangle, rhombus, or square.
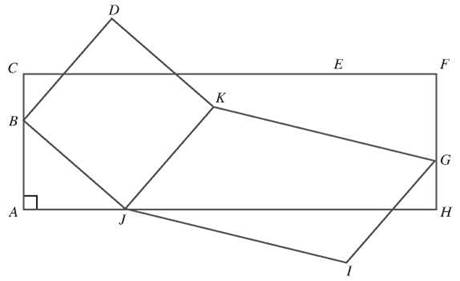
81. ACFH is a quadrilateral with 
and 
ACFH is a _______.
82. BJ = JK = KD = DB. BDKJ is a _______.
83. 
and 
JKGI is a _______.
Find the measurement.
84. In rhombus BDJK, BD = 12 cm. In parallelogram JKGI, GI = _____ cm.
85. Find the area of a parallelogram with a base of 12 inches and a height of 5 inches.
86. ABCD is a trapezoid with 
If m∠A = 58°, find m∠B.
87. In trapezoid ABCD with 
M is the midpoint of 
and N is the midpoint of 
BC = 29 cm and AD = 41 cm. Find the length of 
.
88. PQRS is a trapezoid with 
and 
. If m∠Q= 119°, find m∠S.
89. Find the area of a trapezoid with height of 15 cm and bases 24 cm and 18 cm.
90. The area of a trapezoid is 375 cm2, and the median is 15 cm long. Find the height.
91. Arc 
measures 76°, and ∠APB has its vertex at point P on the circle. Find m∠APB.
92. Tangent 
and tangent 
touch circle O at Qand R and intercept arcs of 59° and 301°. Find m∠QPR.
93. Chord 
intersects chord 
at point X inside circle O. Arc 
measures 24° and arc 
measures 52°. Find m∠MXS.
94. Find the circumference of a circle with radius 7 cm.
95. Find the area of a circle with diameter 24 cm.
Find the surface area of each of the figures described.
96. A square pyramid with side 8 cm and slant height 5 cm.
97. A triangular prism 11 cm high, with bases that are right triangles with legs 18 cm and 24 cm and hypotenuse 30 cm.
98. A cylinder with radius 15 inches and height 22 inches.
99. A cone with radius 5 inches, height 12 inches, and slant height 13 inches.
100. A sphere with a radius of 18 cm.
Find the volume of each of the figures described.
101. A rectangular prism with length 8 inches, width 5 inches, and height 14 inches.
102. A triangular pyramid 42 cm high with a base that is an equilateral triangle 26 cm on each edge, with an altitude of 22.5 cm.
103. A cylinder with a diameter of 20 cm and a height of 48 cm.
104. A cone with a radius of 50 inches and a height of 45 inches.
105. A sphere with a diameter of 60 cm.
Solve.
106. You stand 100 m from the base of a tall building and look up to the top of the building. You measure the angle between your line of sight and the horizontal as 72°. Use trigonometry to find the height of the building to the nearest foot.
107. The tip of the torch of the Statue of Liberty is 305.5 feet above the ground. If you stand on the edge of New York harbor and look to the tip of the torch and find that the angle is 3°, approximately how far from the Statue are you?
108. Jennifer is installing a bird feeder in her yard and wants to steady the pole it sits on by attaching wires to the pole and to stakes in the ground. She wants each wire to form the hypotenuse of a right triangle that is approximately isosceles. If each wire is 10 feet long, how far above the ground should she connect it to the feeder pole?
109. For safe use, a ladder should make an angle of about 75° with the ground. If you want to reach a point 30 feet above the ground and maintain the safe angle, how long should your ladder be?
110. What is the highest point on a wall that a 25-foot ladder can reach if it is placed at the safe 75° angle?