Basic Math and Pre-Algebra
PART 1. The World of Numbers
CHAPTER 3. Order of Operations and Integers
Arithmetic with Integers
Arithmetic with integers may be clearer if you have a sense of owing and having, or gaining and losing. You can use the directional sense of the number line, right and left or up and down, to help as well. We’ll look at each operation and discuss the rules associated with that operation.
Before we begin, let’s address important point about notation. If you write negative numbers with a sign in front, like -7, it would make sense to write positive numbers with a sign in front, like +6. It’s perfectly correct to do that, and sometimes you will see it, but most times, you won’t. You can assume that a number that doesn’t have a sign in front, like 9 or 3, is a positive number, but a negative number, like -5 and -101, will always have a sign to tell you it’s negative. A number with a negative sign is also called a signed number.
Adding Signed Numbers
Adding a positive number to a positive number is nothing new. 4 + 7 = 11, and 73 + 65 = 138. A gain plus a gain is a bigger gain, so a positive number plus a positive number is a positive number. And a loss plus a loss is a loss, so a negative number plus a negative number is a negative number. If you lose $5 and then you lose $8, you’ve lost a total of $13, so -5 + -8 = -13. To put it in formal language, if you’re adding numbers that have the same sign, you add their absolute values and give the answer the same sign as the original numbers.
But what happens when you add numbers with different signs, when you add a positive and a negative? Unfortunately, that’s one of the times when the answer is “it depends.” If you’re playing football and you lose 3 yards on the first play and gain 14 yards on the second, the big gain cancels out the loss and still moves you forward.
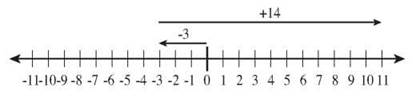
Picture it on a number line (or a football field, if you’re so inclined). Call the line of scrimmage, your starting point, the point we label 0. The first play is a loss of 3, taking you to -3.

Your second play starts from -3 and moves you 14 spaces in the positive direction. The first 3 of those 14 bring you back to 0, and then you continue for another 11 in the positive direction: -3 + 14 = 11. A negative number plus a positive number gave you a positive number.
But what if things were reversed and you gained 3 yards and then lost 14 yards? That’s 3 + -14. Start from 0 again. A gain of 3 moves you 3 to the right, but then the loss moves you back to the left. You give up the 3 you had gained and keep moving left another 11 spaces. 3 + -14 = -11.
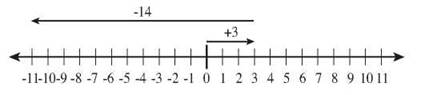
A big gain overpowered a small loss, resulting in a gain, but a big loss overpowered a small gain, leaving you with a loss. In mathematical terms, the number with the larger absolute value dominates the addition and gives its sign to the result. The absolute value of the answer is the difference between the absolute values of those two competing forces.
To add numbers with different signs:
• Subtract the absolute values.
• Take the sign from the number with the larger absolute value.
CHECK POINT
Complete each addition problem. Use a number line to help.
16. -15 + 25
17. 19 + -12
18. -23 + 14
19. -58 + -22
20. 147 + -200
Subtracting Signed Numbers
There’s a simple rule for subtracting signed numbers: don’t. This doesn’t mean you can just ignore those problems. Subtraction, as you saw in the last chapter, is the opposite, or undoing, of addition, and learning a lot of new and separate rules for subtraction is effort you don’t need to expend.
When you’re asked to subtract, add the opposite. Instead of 12 - 8, which you know equals 4, think of 12 + -8, which also equals 4. Then when you’re asked to do -14 - 7, you can just think of -14 + -7 and quickly arrive at -21. 6 – (-3) will become 6 + 3, which is clearly 9. This rule is sometimes referred to as “keep, change, change” because you keep the first number as it is, change to addition, and change the second number to its opposite.
To subtract signed numbers:
• Leave the first number as is.
• Change to addition.
• Change the second number to its opposite.
• Add, following the rules for addition.
CHECK POINT
Complete each subtraction by adding the opposite.
21. -17 – 4
22. 39 – 24
23. 26 – -12
24. -83 – 37
25. -48 – -32
Multiplying and Dividing Signed Numbers
Because multiplication is a shortcut for repeated addition, it’s fair to ask if you can use some of the addition rules to help with multiplication of signed numbers, and because division is the opposite or undoing of multiplication, you’d certainly expect to be able to apply some of the same rules about signs. Let’s look at multiplication first, and then you’ll see that there’s very little more to say about division.
Multiplication is really repeated addition. 5 x 12 means “add 5 twelves together” (or 12 fives, if you prefer). 5 x 12 = 12 + 12 + 12 + 12 + 12, and adding positive numbers gives you a positive number. 5 x 12 = 60. Nothing new there.
What if you multiply a positive number by a negative number? What is 3 x -4? It means “add 3 copies of the number -4” or “take 3 losses of 4 each.” That’s -4 + -4 + -4, and adding negative numbers gives you a negative. 3 x -4 = -12. If you’re wondering what to do with a negative times a positive, like -5 x 7, remember that multiplication is commutative. -5 x 7 = 7 x -5 = -35, and no new rules are necessary.
When you multiply a negative number by a negative number, remember that the negative sign means “the opposite of.” This means -5 x 7 is the opposite of 5 x 7, or the opposite of 35, or -35. If both numbers are negative, as in -2 x -4, you’re asking for the opposite of 2 x -4. You know that 2 X -4 is -8, and the opposite of that is 8. -2 x -4 = 8. A negative multiplied by a negative is a positive.
To multiply signed numbers, multiply the absolute vales and follow these rules for signs.
Positive x Positive = Positive
Positive x Negative = Negative x Positive = Negative
Negative x Negative = Positive
If you’re multiplying more than two numbers, you can save some time by counting the number of negative signs. If the number of negatives is even, the product will be positive. If the number of negatives is odd, the product will be negative. For example, -2 x -5 x -3 x -1 = (-2 x -5) x (-3 x -1) = 10 x 3 = 30. Four negatives, an even number, make a positive. But put one more negative into the problem and you have -2 x -5 x -3 x -1 x -4 = (-2 x -5) x (-3 x -1) x -4 = 10 x 3 x -4= 30 x -4 = -120. With an odd number of negatives, your answer is negative.
WORLDLY WISDOM
A quick way to remember the rules for multiplying integers: multiply same signs, your answer is positive; multiply different signs, it's negative.
CHECK POINT
Complete each multiplication problem.
26. -4 x 30
27. 8 x -12
28. -7 x 15
29. -11 x -43
30. -250 x 401
You’ll be pleased to know that the rules for division of signed numbers are the same as the rules for multiplication, except that, obviously, you divide the absolute values instead of multiplying.
To divide signed numbers, divide the absolute values and follow these rules for signs.
Positive ÷ Positive = Positive
Positive ÷ Negative = Negative ÷ Positive = Negative
Negative ÷ Negative = Positive
Following those rules, you can see that 42 ÷ 6 = 7, and 84 ÷ -4 = -21. -15 ÷ 5 = -3, but -15 ÷ -5 = 3.
CHECK POINT
Complete each division problem.
31. 49 ÷ -7
32. -125 ÷ -15
33. -27 ÷ 9
34. 120 ÷ -6
35. -981 ÷ -9
The Least You Need to Know
• When completing an arithmetic problem, follow the order of operations: parentheses first, then exponents, then multiplication and division, and lastly, addition and subtraction.
• The distributive property says that when you need to add two numbers and then multiply by a third, you can choose to multiply each of the first two by the third and then add. You’ll get the same answer.
• The absolute value of a number is its distance from zero on the number line.
• To add integers with the same sign, add the absolute values and keep the sign.
• To add integers with different signs, subtract the absolute values and take the sign on the number with the larger absolute value.
• To multiply or divide integers, multiply and divide without the signs. Then it the signs of the two numbers are the same, your answer is positive. If the signs are different, your answer is negative.