Mathematics for the liberal arts (2013)
Part I. MATHEMATICS IN HISTORY
Chapter 3. MODERN MATHEMATICS
3.2 The 18th Century: Consolidation
Introduction
The 18th century saw the continuation of the Scientific Revolution of the previous century. Newtonian physics was triumphant, and scientists worked to apply the new scientific method to other fields. Equally important was the birth of the Industrial Revolution, which, together with the new science, was eventually to transform everyday life in ways more profound than anything since the advent of agriculture.
France was the dominant political and cultural center of 18th century Europe. It was the richest and second most populous (after Russia) country in Europe. Early in the century, the French had expanded their colonial holdings overseas, but lost most of them in the Seven Years’ War (1756–63). This war, which pitted France, Austria, and Russia against Britain and Prussia, took place on several continents and killed about a million people. In India, the war was called the Third Carnatic War, and ended with the English East India Company establishing dominance over the other European traders. (The height of English colonialism in India was not until the 19th century.) In the American theater, the war is called the French and Indian War; it established English control of Canada.
In 1789 the French Revolution began, the central political conflict in the modernization of Europe, specifically the reduction in power of the royalty and the Church. On July 14 the revolutionaries attacked the prison and armory called the Bastille. A decade of political unrest followed. At the beginning, the king remained in place, but was forced to cede some power to the National Assembly. The members of the Assembly sat in two sections, the supporters of the king and church on the right, and the supporters of the revolution on the left. This was the origin of the custom of dividing political factions into the left and the right.
Unrest continued, eventually leading to the execution of the king in 1793. This was followed by the Reign of Terror (1793–94), during which many thousands were executed by guillotine. France was also engaged in wars with its neighbors, whose kings were not too happy with the ideas of the revolution. After some initial defeats, the French army was victorious. One of its generals, Napoleon Bonaparte, took control of France in 1799.
In Eastern Europe, this century saw the rise of Prussia and Russia, at the expense of Poland. The Kingdom of Prussia was formed in 1701 and transformed into a world power especially by Frederick the Great (r. 1740–86). Frederick was a great patron of science and the arts; he himself was a flutist and composer. He also was interested in philosophy and an admirer of the Enlightenment (see below).
Russia greatly expanded its empire under Peter the Great, who ruled 1682–1725 (jointly with his half-brother until 1696, when he was 24 years old). In addition to his conquests, he modernized Russia, adapting much from Western Europe, and founded St. Petersburg, modeled after the canal city of Venice. This city hosted the greatest of 18th century mathematicians, Leonhard Euler (1707–1783).
The other Eastern European power was the Hapsburg empire based in Austria. Although the Hapsburgs had their political difficulties in this century, their capital, Vienna, was a major cultural center, notable especially for its musical luminaries, including Haydn, Mozart, and Beethoven.
The Industrial Revolution began in England. It was preceded and.made possible by an “Agricultural Revolution,” which increased agricultural efficiency and made available the labor to work in the new industrial factories. There were many aspects to the new agriculture, which were added gradually over the centuries. These included new crops from America, improved crop rotation, better transportation, increased availability of financing, and new mechanical inventions. In 1701 Jethro Tull introduced his horse-drawn seed drill, which placed seeds more efficiently in rows, at the right depth, and covered them with soil. Several improvements were made to the plow during this century, and there was increased use of iron plows, which replaced wooden plows. In 1784 Andrew Meikle invented the threshing machine, used to separate the grain from the rest of the plant.
The Industrial Revolution was powered by coal, of which England had an abundance. In 1709 Abraham Darby I built a blast furnace at Coalbrookdale that used coke, a fuel derived from coal, to produce pig iron. The coke replaced charcoal made from wood. This, and other technical innovations throughout the century, made iron increasingly available for the tools of the Industrial Revolution.
A central technology of the early Industrial Revolution was the steam engine, which used a coal fire to heat water into steam, which in turn drove a piston to do the work. The first commercially successful steam engine was introduced around 1712 by Thomas Newcomen. It was used primarily in coal mines. As the shallower coal seams were exhausted, miners needed to dig deeper to mine the coal. These mines often flooded; the new steam engines were used to pump out the water. In 1769 James Watt invented an improved steam engine. By 1800 his firm had produced 496 engines, mostly powering machinery in mills.
The textile industry underwent major developments in this century, turning it from a cottage industry into a factory industry. The spinning jenny, introduced in 1764 by James Hargreaves, made the process of producing yam from wool more efficient. Richard Arkwright built the first cotton mill, a factory combining spinning and weaving machines. In 1794 the American Eli Whitney patented the cotton gin, which separated the seed from the cotton fiber.
The 18th century is also called the Age of Enlightenment. Enlightenment was a philosophy that emphasized the rational over the supernatural. It promoted science and opposed superstition. The Enlightenment had its origins in the 17th century, in the works of the philosophers Baruch Spinoza (1632–1677) and John Locke (1632–1704), as well as the new science. Its apex, however, was in the 18th century, throughout Europe and North America, but centered in France. Among its stars were the writer Voltaire (1694–1778), the philosopher Jean-Jacques Rousseau (1712–1778), and Denis Diderot (1713–1784), editor of the influential Encyclopédie, ou dictionnaire raisonné des sciences, des arts et des métiers (Encyclopaedia or a Systematic Dictionary of the Sciences, Arts and Crafts). This was a 35-volume work, first published between 1751 and 1772, which attempted to include all of the world’s knowledge. Its many contributors included all the leading lights of the French Enlightenment.
The Enlightenment had a political aspect as well, one which rejected the divine right of kings and emphasized the consent of the governed, and the ideals of freedom and equality. These ideals were expressed in the American Declaration of Independence (1776) and the French Declaration of the Rights of Man and the Citizen (1789). They inspired the world’s first modem liberal democracy, the United States of America.
The 18th century witnessed a remarkable collection of intellects in Scotland, beginning with the philosopher Francis Hutcheson (1694–1746). This group included the philosopher David Hume (1711–1776), the poet Robert Bums (1759–1796), the geologist James Hutton (1726–1797), the chemist Joseph Black (1728–1794), and the philosopher Adam Smith (1723–1790), whose 1776 work An Inquiry into the Nature and Causes of the Wealth of Nations is considered the beginning of modem economics. Also native to Scotland were the inventors James Watt (1736–1819) and Andrew Meikle (1719–1811).
In science, the 18th century saw the birth of modem chemistry with the work of Joseph Black (1728–1799), Joseph Priestley (1733–1804), and especially Antoine Lavoisier (1743–94) (who was executed in the Reign of Terror); they isolated oxygen, nitrogen, hydrogen, and carbon dioxide, and discovered the law of conservation of mass.
Modem geology was also bom, inspired in part by mining. At the beginning of the century, the most popular theory traced geological origins to the biblical flood. During the century, an effort was made to establish a strictly scientific basis for geology. The year 1795 saw the publication of James Hutton’s An Investigation of the Principles of Knowledge and of the Progress of Reason, from Sense to Science and Philosophy, whose 2138 pages developed theories of the origin of rocks, including sedimentary rocks formed in the sea and later raised up, concluding that the Earth was in fact much older than the biblical few thousand years, and still geologically active.
Research in electricity accelerated in the 18th century, helped considerably by the invention of the Leyden jar, a device for storing charges. The connection of electricity to lightning was discovered by Benjamin Franklin (1706–1790), and to frog muscles by Luigi, Galvani (1737–1798). Charles-Augustin de Coulomb (1736–1806) discovered his famous law, a formula for the force between two charges at a given distance. The century ended with the invention of the first electric battery by Alessandro Volta (1745–1827).
In mathematics, much work was done to consolidate the advances of the previous century. This included reconciling the different versions of calculus presented by Newton and Leibniz. Scientists also continued refining and extending the Newtonian theory of mechanics, which describes how bodies move when acted upon by forces. This theory was as much mathematics as physics. The typical application used Newton’s laws to arrive at a type of equation, called a differential equation. Then the hard work began, studying the differential equation to extract useful formulas giving the motion of the bodies. Such studies were carried out on planets and moons, on violin strings and drums.
In addition to differential equations, important advances were made in this century in number theory, especially by Euler. He and others also studied the complex numbers earlier investigated by Bombelli. In fact, complex numbers became one of the most important topics in mathematics right through the 19th century.
Finally, we note that this century was characterized by a major split between British and Continental mathematicians, which began with a priority dispute between Newton and Leibniz over the invention of the calculus. As a result, even though science was well represented in the British Isles, most of this century’s mathematics was developed on the Continent.

The Budding of 18th Century Mathematics
The invention of Calculus in the previous century by Isaac Newton and Gottfried Leibniz ushered in a new way of approaching both mathematics and physics. Eminent in this endeavor were the illustrious Bernoulli family.
James (1654–1705) and John (1667–1748) Bernoulli
Probably no other single family has produced so many capable mathematicians as the Bernoulli family. As many as eight different members of this Swiss family were mathematicians of note, beginning with the brothers James (Jacob) and John (Johann). Many of them were widely known, as this story illustrates.
Once, while traveling with a learned stranger who asked his name, he said, “I am Daniel Bernoulli.” The stranger could not believe that his companion actually was that great celebrity, and replied [in jest], “I am Isaac Newton.”1
Though their father wished James to study theology and John to study medicine, both eventually pursued mathematics, particularly the new calculus of Leibniz. In Basel, Switzerland, James was professor of mathematics from 1687 until his death in 1705. He was succeeded in that post by his younger brother John, who, until that time, had taught at Groningen, Holland.
![]()
Figure 3.7 A logarithmic spiral.

James Bernoulli was responsible for several notable mathematical achievements. He was perhaps the first mathematician to actively use polar coordinates to solve problems. He studied many special curves including the catenary (hanging chain) and the lemniscate (figure eight), but he was particularly interested in the logarithmic spiral, which has the polar equation r(θ) = aebθ (see Figure 3.7). He even asked that the spiral be engraved on his tombstone, cleverly referring to the way the curve looks like a copy of itself when magnified via the epitaph, “I shall arise the same, though changed.”2
James also had an interest in series. He proved that the harmonic series diverges (i.e. it has an infinite sum).
![]()
He also determined that the reciprocals of the squares have a finite sum, though it was Euler (a student of his brother John) who finally discovered the actual value to be π2/6.
![]()
One of James Bernoulli’s most famous results is the “Law of Large Numbers,” which is sometimes referred to simply as Bernoulli’s Theorem. It states:
If the probability of an event is p, and if n independent trials are made, with k successes, then ![]() → p as n → ∞.
→ p as n → ∞.
An easy way to think about Bernoulli’s Theorem is to consider a fair coin. Call flipping heads a “success.” Although the probability of heads is 50%, if you flip a coin 10 times, you may get any number of heads (successes) and tails (failures), even 10 heads in a row. However, the theorem guarantees that no matter what has happened with any finite number of flips, as you flip more and more, the proportion of heads will always tend (eventually) toward 50%.
Together, James and John made many contributions to the early calculus, sometimes in collaboration and often in competition. The brothers were regular correspondents with Leibniz, and together the three men discovered what would today constitute much of a college course in calculus.
Figure 3.8 A cycloid.
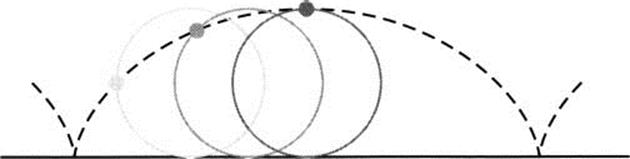
In 1696 John Bernoulli proposed the brachistochrone problem as a calculus challenge to Newton. It was addressed, “to the shrewdest mathematicians in the world.” The problem can be stated,
Let two nails in a wall, one not directly above the other, be connected by a wire. Find the shape of the wire that allows a (frictionless) bead to fall from the higher point to the lower in the least amount of time.
John knew, via calculus, the answer to be a cycloid (actually, an upside-down cycloid), which is a curve traced by a fixed point on a rolling circle, as in Figure 3.8. The challenge was correctly solved by four other mathematicians: his brother James, Leibniz, Newton, and l’Hôpital.
John Bernoulli was also indirectly responsible for the content of the world’s first calculus text, because as tutor to Guillaume de l’Hôpital (1661–1704), he contributed many of the ideas that were incorporated into l’Hôpital’s book, Analyse des infiniment petits, published in 1696.
Complex Numbers
A recurring theme in the history of mathematics is the expansion of what we consider to be a number. We have seen this theme played out when the Pythagoreans discovered the existence of irrational numbers. The theme occurred again when zero was invented in China and India. As we saw at the end of Chapter 2, acceptance of square roots of negative numbers came about through the solution of cubic and quartic equations. Mathematicians defined a new number, i, such that i2 = – 1. Certainly, i is not a real number, since the square of a real number is always nonnegative. It is called an imaginary number. A complex number is a number of the form a + bi, where a and b are real numbers. Complex numbers, at first regarded with skepticism, were fully incorporated into mathematics once Caspar Wessel (1745–1818) and Jean-Robert Argand (1768–1822) showed that the new numbers are not mysterious at all. They can be plotted on a Cartesian coordinate plane, with the horizontal axis giving the real part of the number and the vertical axis the imaginary part. See Figure 3.9.
As if to close the deal, Carl Friedrich Gauss (1777–1855) proved that every polynomial of degree n has n complex roots (the Fundamental Theorem of Algebra). For example, the quartic polynomial
![]()
Figure 3.9 The complex plane.
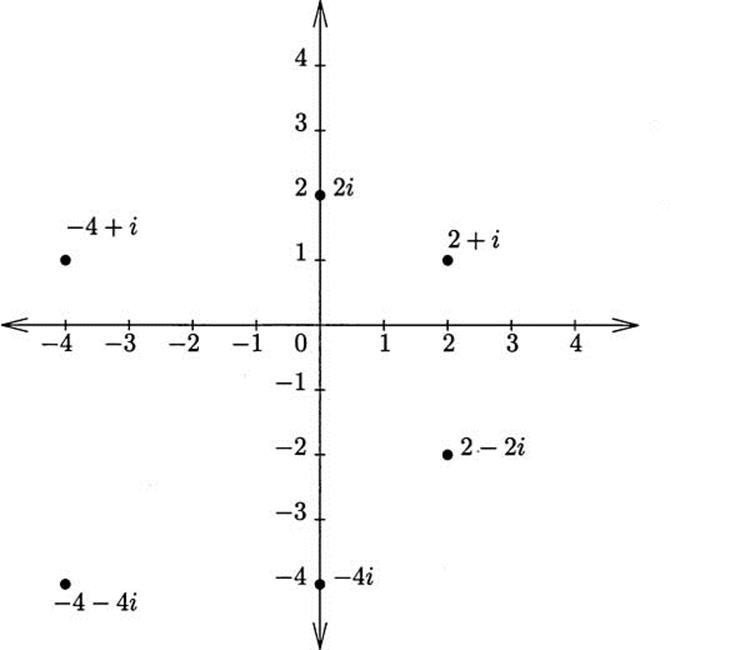
has four roots, two real roots, 2 and 3, and two complex roots, 1 + i and 1 – i. Thus the quartic factors as
![]()
Complex numbers have elegant geometric properties. The addition of complex numbers is quite simple. To add two complex numbers, add their real parts and add their imaginary parts. This is a vector addition. Multiplication is more interesting. Take, for example, the case of multiplication by i. The product of 1 by i is i; the product of i by i is – 1. This means that the unit vectors on the real and imaginary axes are rotated 90° counterclockwise. Indeed, multiplication by i rotates the entire plane 90° counterclockwise. Multiplication by a real number, on the other hand, stretches each complex number by that number. Multiplication by an arbitrary complex number stretches and rotates each complex number. Thus, we may think of multiplication as stretching and twisting the complex plane.
Complex numbers are instrumental in many branches of mathematics, as well as in applied fields such as electrical engineering. The imaginary has proved to be eminently practical.
Euler
Read Euler, read Euler, he is the master of us all.
PlERRE-SlMON DE LAPLACE (1749–1827)
Leonhard Euler (1707–1783) was the most prolific mathematician in history, and one of the best. He contributed to many areas of mathematics, and, although he never had a teaching job, his texts have been immensely influential in mathematics education.
Euler helped change the emphasis in calculus from studying curves to studying functions. He originated the now ubiquitous notation f(x). He was the first to treat sine and cosine as functions, instead of just lengths. For example, we now can write x(t) = sin t, where iisa number, not necessarily an angle. This notion is quite important in physics, where, for example, x may measure the position of an object at time t.
Leonhard Euler (1707–1783)
Leonhard Euler was bom in Basel, Switzerland, the son of a Protestant minister. He was a child prodigy, graduating from the University of Basel at age fifteen. Although his father originally intended for him to become a minister, Leonhard showed an early interest in mathematics. This was nurtured by contact with a family friend, Johann Bernoulli. In 1726 Euler joined Nicolaus and Daniel Bernoulli, sons of Johann, at the St. Petersburg Academy of Sciences. He worked in Russia until 1741, when he joined the Berlin Academy of Sciences. In 1766 he returned to St. Petersburg, where he spent the rest of his life.
In addition to his mathematics, Euler produced important work in physics, engineering, and astronomy. He helped create improved lunar tables, which were used to solve the difficult problem of determining longitude at sea. He wrote a successful work of popular science. After he returned to Russia, he became almost completely blind, but was still able to perform involved calculations in his head, and continued his prodigious output of research until his death.
![]()
Euler spent much time studying logarithms and exponential functions, which were quite important in solving a variety of differential equations. (Exponential functions are of the form f(x) = ax, where a is some constant, called the base.) Euler discovered a remarkable connection between these functions and trigonometric functions.
To state Euler’s discovery, we need to introduce one of the most important mathematical constants: e. We consider a simple problem in compound interest. Suppose that we invest $1 at 100% interest. After 1 year, we might have $2, the original $1 plus $1 in interest. But suppose that our interest was figured twice a year. After six months, we would have earned fifty cents interest, so would have $1.50. In the next six months, we would earn 50% more, but on the full $1.50; in other words, we would earn another $.75, for a total of $2.25.
Suppose now that we figure (“compound”) interest three times. After four months, we have 1 + 1/3 dollars. After eight months, we have
![]()
dollars. After one year, we have
![]()
dollars, approximately $2.37.
It is clear that the more times we compound the interest, the more money we have at the end, because we are earning interest on more interest. Does this mean that we can earn as much as we like, by compounding more often? Unfortunately, no; we get at most about $2.72. As we compound more and more often, the amount of money at the end gets closer and closer to our number e, which is approximately 2.718281828. Put another way, the limit of (1 + l/n)n, as n goes to infinity, is e. In passing, we note another nice formula.
![]()
Euler was able to define an exponential function with e as the base. He could even deal with powers of e that are complex numbers. The connection to trigonometric functions that he found was this:
![]()
where x is given in radians. For example, if x = π, then sin x = 0 and cos x = – 1, so eπi – 1, or
![]()
This is called Euler’s Identity. Remarkably, it ties together the five most important numbers in mathematics: 0,1,π, e, and i.
Euler also solved a famous problem posed in 1644, the Basel Problem. The problem was to compute the sum
![]()
He showed that the sum is π2/6. In fact, his method could be used to find the sum
![]()
for any positive even integer n. He also tried to compute
![]()
but was unsuccessful. Nobody knows what this sum is even today, although it has been proved to be an irrational number.
Finally, we mention an important formula in geometry discovered by Euler. This concerns polyhedra, solids with flat faces and straight edges. An example is a cube. Let us denote by V the number of vertices (comers) of a polyhedron, by E the number of edges, and by F the number of faces. So in the case of a cube, V = 8, E = 12, and F = 6. (Check!) What Euler discovered is the formula V – E + F = 2 for polyhedra with no holes. Although he published a proof of this, it was incomplete. The first complete proof was given by Adrien-Marie Legendre (1752–1833) in 1794.
This formula has a nice application to the classification of Platonic solids. Recall that the five Platonic solids (Figure 3.10) were constructed in Euclid’s Elements. These polyhedra have the following two properties:
Each vertex is the endpoint of the same number of edges, which we denote by m.
Each face is bounded by the same number of edges, which we denote by n.
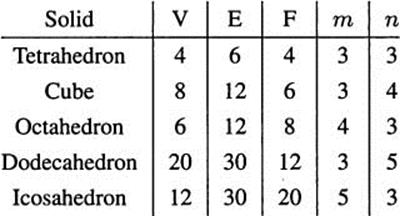
For a cube, m = 3 and n = 4. Figure 3.11 shows V, E, F, m, and n for the Platonic solids.
Figure 3.10 The Platonic solids.
Figure 3.11 Parameters for the Platonic solids.
We will use the two conditions above, and V – E + F = 2, to show that there can only be these five Platonic solids. First, note that each edge has two endpoints, so if we add up all edge-vertex pairs, we get 2E. Since each vertex is the endpoint of m edges, that same sum is mV. In other words, 2E = mV.
Similarly, each edge bounds two faces, so if we add up all edge-face pairs, we get 2E. Since each face is bounded by n edges, that same sum is nF. In other words, 2 E = nF.
Let us use the last two results to substitute for F and V in V – E + F = 2.
![]()
Divide by 2E.
![]()
Add 1/2 to both sides.
![]()
Since each vertex is the endpoint of at least three edges, m ≥ 3. Since each face is bounded by at least three edges, n ≥ 3. Suppose that m and n were both greater than 3. Then
![]()
Since 1/E > 0, this clearly is impossible. So we must have m = 3 or n = 3.
If m = 3, we must have n < 6, since l/n + 1/3 > 1/2. The three cases n = 3,4,5 yield the tetrahedron, cube, and dodecahedron, respectively.
If n = 3, we must have m < 6. The three cases n = 3,4,5 yield the tetrahedron, octahedron, and icosahedron, respectively. Therefore, these are the only possible Platonic solids.
Euler’s influence on mathematics was huge. One last example: Euler introduced the notation π for the ratio of the circumference of the circle to its diameter.
Number Theory
Another area of mathematics that Euler advanced was number theory, the branch of mathematics that studies properties of the positive integers. Among other contributions, he provided proofs for a number of theorems that Fermat stated without proof. He also proved Fermat’s Last Theorem for the case n = 3, i.e., that there is no nontrivial integer solution to x3 + y3 = z3.
The other mathematician of this century who was in Euler’s class was Joseph- Louis Lagrange. Like Euler, Lagrange contributed to many areas of mathematics. In number theory, he proved a number of important results, including several stated without proof by Fermat and others.
Joseph-Louis Lagrange (1736–1813)
Joseph-Louis Lagrange was bom Giuseppe Luigi Lagrangia, in Turin, Italy. His family was French on his father’s side, and he later adopted the French version of his name. Like Euler, Lagrange was a prodigy. He became a lecturer in mathematics at the Royal Artillery School of Turin at age nineteen.
In 1766, when Euler left Frederick the Great’s Berlin Academy to return to St.Petersburg, Lagrange replaced him. He stayed in the Prussian capital until Frederick’s death in 1787. He then accepted an invitation to Paris, where he was given apartments in the Louvre. It was in Paris that he finished his great work, Mécanique Analytique.
In Mécanique Analytique (Analytic Mechanics), published in 1788, Lagrange reformulated Newtonian mechanics. The new formulation made use of an extension of calculus called the calculus of variations, which Euler and Lagrange had developed. Although this was a work of mathematical physics, Lagrange himself viewed mechanics as a branch of pure mathematics. The Mécanique Analytique was the basis of all subsequent work in the area. It was so beautifully done that William Rowan Hamilton (1805–1865) called it a “kind of scientific poem.”
Besides his work in mathematics and mechanics, Lagrange contributed to astronomy, and to education. Since he was nonpolitical, he survived the crazy years following the French Revolution, unlike his chemist friend Lavoisier, who was guillotined. Lagrange helped develop the metric system and reform science education in France.
![]()
One theorem of number theory proved by Lagrange was Wilson’s theorem, discovered around 1770 by John Wilson (1741–1793), an English mathematics professor. Wilson did not realize that the theorem was known to Ibn al-Haytham around 1000, and even earlier to Bhaskara I in the 7th century. Such is the vagary of naming in mathematics. Wilson gets the credit, even though he wasn’t the original discoverer, nor did he prove the theorem. It was Lagrange who proved it.
Wilson’s theorem is a criterion by which we can tell whether an integer is a prime number. An integer n, greater than 1, is prime if and only if (n – 1)! + 1 is a multiple of n. (Wilson only stated the “if” part of the theorem.) For example, 7 is prime, and (7 – 1)! + 1 = 721, a multiple of 7. On the other hand, 6 is not prime, and (6 – 1)! + 1 = 121, not a multiple of 6. The only shortcoming of Wilson’s theorem is that the computation of (n – 1)! takes too long for the criterion to be useful. However, early in the 21st century, an effective procedure was found for determining when a positive integer is prime.
Also around 1770 Lagrange proved that every positive integer is a sum of four squares. For instance, 97 = 82 + 5 2 + 22 + 22. Here is a challenge: How many ways can you write 10 as a sum of four squares, where the order of the terms matters, and the numbers being squared can be positive or negative? For example, 32 + 12 + 02 + 02, 32 + 02 + 02 + l2 and (–3)2 + l2 + 02 + 02 are all considered different. See the next section for the answer.
One of the most important theorems of number theory was conjectured in 1796 by Adrien-Marie Legendre (1752–1833). It is called the Prime Number Theorem, and has to do with the distribution of prime numbers. It says that the number of prime numbers less than a given number n is approximately n/ln n, where In n is the natural logarithm of n. For example, the number of primes less than 106 (one million) is approximately 72,382, whereas the actual number is 78,498 (an error of about 8%). The relative error decreases as n increases. As we will report in Section 3.3, the Prime Number Theorem was proved about 100 years after it was conjectured. A new machinery was needed for the proof: complex variables.
Paris
Paris was the premier center of mathematics in this century. Among its illustrious mathematicians, in addition to Lagrange, were Alexis Clairaut (1713–1765), Jean Le Rond d’Alembert (1717–1783), Gaspard Monge (1746–1818), Pierre-Simon de Laplace (1749–1827), and Adrien-Marie Legendre (1752–1833).
Pierre-Simon de Laplace (1749–1827)
Pierre-Simon de Laplace was bom at Beaumont-en-Auge, in Normandy, France, the son of a farmer. He studied at the University of Caen, then went to Paris in 1769, with a letter of recommendation to the mathematician Jean d’Alembert. With the help of d’Alembert, he obtained a professorship at the École Militaire in Paris.
Laplace’s greatest accomplishments were in mathematical physics. In particular, he worked on the problem of the stability of the solar system. Newton had determined the larger motions of the solar system, due to the gravitational attraction of the Sun on the planets, but understood that the planets interacted among themselves. He despaired of solving this more general problem exactly, and in fact opined that divine intervention was necessary from time to time to maintain the system’s stability. Laplace, in a series of papers, showed that the solar system was on average stable. (This was not the final word, as Poincaré demonstrated one hundred years later that the solar system is in fact chaotic.)
In the process of rewriting celestial mechanics, Laplace developed a number of new mathematical techniques. His influence is memorialized in terms such as the Laplace transform and Laplace’s equation, which every undergraduate mathematics and physics major encounters. In addition, Laplace did groundbreaking work in probability and statistics. He also took time in 1780, in joint research with the chemist Antoine-Laurent Lavoisier, to demonstrate that respiration is a form of combustion.
![]()
The leading mathematicians of the day did not work at universities. The modem research university was a 19th century invention. The best education in science and mathematics in 18th century France was provided at military schools, which trained engineers. The best research was done at academies, especially at the Paris Academy of Sciences.
Many of the military schools and universities were closed during the French Revolution. The need for education did not disappear, however. In 1794 the École Centrale des Travaux Publiques was founded. Shortly after, it was renamed the École Polytechnique. Monge was heavily involved in developing the curriculum, and most of the leading French mathematicians of the time taught there, including Lagrange and Laplace. The École Polytechnique became a model for engineering schools worldwide.
The 1790s also saw the invention of the metric system. Lagrange was the president of the committee that established the metric system. Laplace and Monge also served on this committee.
EXERCISES
3.20 Find the sum and product of the complex numbers 2 + 3i and 3 + 2i. Find the quotient (2 + 3i)/(3 + 2i) in the form a + bi.
3.21 Explain what happens geometrically when the complex number 3 + i is multiplied by –i. Do the same for multiplication by 2i.
3.22 Find all four roots of the quartic polynomial x4 – x3 + x2 – x.
3.23 Can you give an example of a quartic polynomial with no real roots?
3.24 Give a quintic polynomial with roots 0,1, –1, i, and – i.
3.25 What is eπi/2?
3.26 What is e4πi?
3.27 A soccer ball is a polyhedron. Find the values of V, E, and F for it.
3.28 Give an example of a polyhedron, other than the dodecahedron, such that V = 20, E = 30, and F = 12.
3.29 Give an example of a polyhedron, other than the icosahedron, such that V = 12, E = 30, and F = 20.
3.30 Use Euler’s solution of the Basel Problem to find the sum of the infinite series
![]()
3.31 Verify Wilson’s theorem for n = 5, 8, 9,10, and 11.
3.32 How many ways can you write 4 as a sum of four squares, where the order of the terms matters, and the numbers being squared can be positive or negative? Can you answer the same problem for the number 10?