Mathematics for the liberal arts (2013)
Part I. MATHEMATICS IN HISTORY
Chapter 4. CALCULUS
4.5 Formulas for Derivatives
We saw in Section 4.3 that slopes can be used to compute tangible things such as velocities of objects. In Section 4.4 we created a formal mathematical process for finding slopes, called differentiation. Since derivatives are the key to solving all kinds of mathematical problems, it is natural to want to know the derivative of as many different kinds of functions as possible. However, even the most mathematical of us eventually find it tedious to compute derivatives using the limit definition. Luckily, there are easily recognizable patterns that we can use as shortcuts, or “derivative rules.”
The Constant Rule
The simplest derivative rule is that the derivative of a constant function f(x) = c is f′(x) = 0. The graph of a constant function f(x) = c is a horizontal line that intersects the y-axis at the value c. Since it is a horizontal line, it has a slope of 0 everywhere. That is, at every x the slope is zero. This is precisely what f′(x) = 0 means (it gives 0 for every value of x).
The Line Rule
Non-horizontal lines are just as easy. The derivative of a linear function f(x) = mx is f′(x) = m, since f is a line through the origin with slope m. Of course, nothing changes if the y-intercept happens to be different from 0 (i.e., if the line doesn’t go through the origin); it still has slope m. We can write this idea as a rule, and we have our first rule of derivatives.
The line rule: If f(x) = mx + b, then f′(x) = m.
Notice that the line rule contains the constant rule within it. If f(x) = b is a constant function, then the line rule tells of that f′(x) = 0. For example, if f(x) = 7 = 0x + 7 is a horizontal line (with y-intercept 7), then its derivative is zero.
![]() EXAMPLE 4.5
EXAMPLE 4.5
We can check the line rule carefully, using the definition of derivative. If f(x) = mx + b, then the definition of derivative tells us that
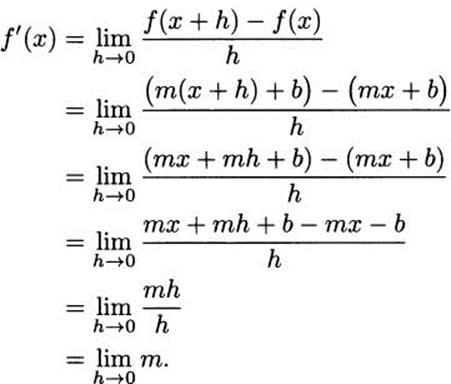
It feels a little strange to ask what m is getting close to as h becomes closer and closer to 0, since m is just a number, but it’s perfectly correct to declare that it gets close to m. You might say that being exactly equal to something is the very best way to get close to it.
So we get f′(x) = m. Of course, a slope of m is exactly what our experience tells us to expect for the line f(x) = mx + b.
The Sum Rule
It might have occurred to you that the function f(x) = mx + b is actually the sum of two lines, a non-horizontal line g(x) = mx and a horizontal line h(x) = b. Using the line rule for each, we get g′(x) = m and h′(x) = 0. Notice that if we add these derivatives, g′(x) + h′(x) = m, which happens to be the same as f′(x). This is not a coincidence, but is our second rule of derivatives.
The sum rule: The derivative of a sum is the sum of the derivatives:
![]()
![]() EXAMPLE 4.6
EXAMPLE 4.6
Since 3x = 2x + x, we can use the line rule directly to determine that (3x)′ = 3, but we can also use the sum rule (and the line rule) on the right hand side to get (3x)′ = (2x)′ + (x)′ = 2 + 1 = 3. It doesn’t matter which rules we use, we always get the same answer for the derivative.
If your algebra skills are good, you can verify the sum rule using the limit definition:
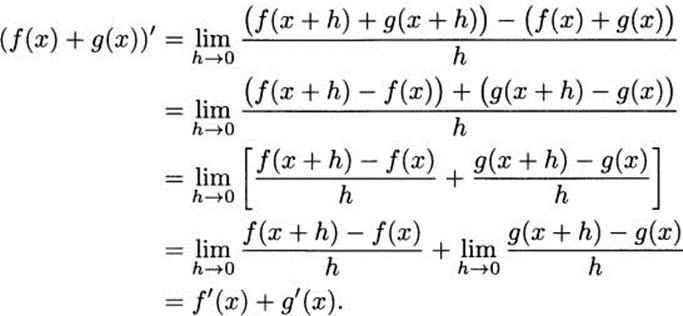
![]() EXAMPLE 4.7
EXAMPLE 4.7
The sum rule works for three (or more) terms as well. For example, take f(x) = x + x + x. We can group with parentheses, to make this a sum of just two terms, f(x) = x + (x + x). Then an application of the sum rule tells us

The key observation is that this pattern always works, no matter what functions you use. So (f(x) + g(x) + h(x))′ = f′(x) + g′(x) + h′(x).
The Power Rule
In Example 4.4 we discovered that (x3)′ = 3x2. Before that, in Example 4.3 we determined that (x2)′ = 2x. The line rule tells us that (x1)′ = 1, since x1 is another way of writing x. And because x0 = 1 we can see that (x0)′ = 0. Perhaps you have already determined that these all adhere to a common pattern.
The power rule: For any integer n ≥ 0, the derivative of the power function f(x) = xn is f′(x) = nxn–1.
![]() EXAMPLE 4.8
EXAMPLE 4.8
Let’s find the derivative of f(x) = x10. By the power rule, we have
![]()
![]() EXAMPLE 4.9
EXAMPLE 4.9
Find the derivative of f(x) = x3 + x2 + 3x + 7.
Solution: By the sum rule, we have

The Constant Coefficient Rule
There is a straightforward differentiation rule for multiplying functions by constants.
The constant coefficient rule: If c is a constant, then (cf(x))′ = cf′(x).
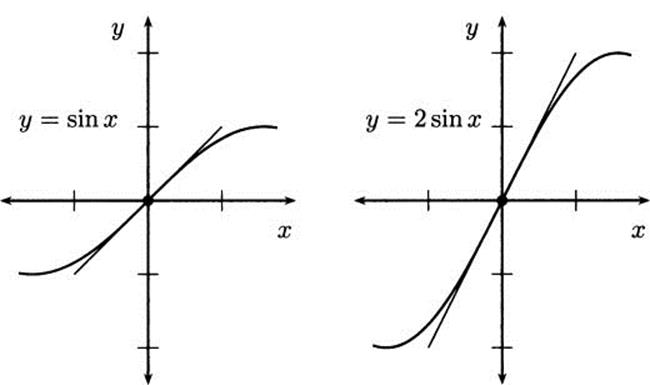
In terms of the graph, multiplying a function by some constant has the effect of stretching (or compressing) it vertically. For example, the function f(x) = 2sin x is twice as tall as a standard sine curve. What the constant coefficient rule tells us is that the coefficient applies to slopes in the same way. Examine Figure 4.10 to see that this seems plausible.
Figure 4.10 Slopes on 2 sin x are twice the size of slopes on sin x.
Intuitively, slope is always a calculation of “rise over run.” If we multiply a function by the constant 5, then in slope calculations the “rise” changes by the same factor of 5 (because all of the y-values are 5 times as large), but the “run” is the same. The new slope would look something like
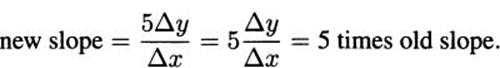
This agrees with what we already know from the line rule. By the line rule, we know that the derivative of 7x is 7. The constant coefficient rule tells us that we can also think of it as 7 times the derivative of x. Of course 7(x)′ = 7 · 1 = 7, so we get the same answer.
In the same way, the constant coefficient rule tells us that (5x3)′ = 5(x3)′ = 5 · 3x2 = 15x2.
Derivatives of Polynomials
The power rule, sum rule, and constant coefficient rule combine to tell us everything we need to take the derivative of any polynomial. At first, we should probably compute derivatives step by step, but soon we’ll be taking derivatives almost effortlessly.
![]() EXAMPLE 4.10
EXAMPLE 4.10
Let’s find the derivative of f(x) = 7x5 + 16x4 – 32x + 100. By the sum rule, we know that
![]()
The constant rule tells us that (100)′ = 0, and the constant coefficient rule lets us “pull out” the constant from each of the other terms we are taking the derivative of, so
![]()
Finally, applying the power rule,
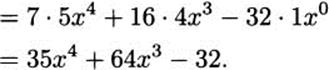
![]() EXAMPLE 4.1l
EXAMPLE 4.1l
While we are building these differentiation rules, we should not get caught up in the letters we use. Functions do not have to be called f and their variable does not have to be x. The rules apply in the same ways if we use other variable and function names. For example, the derivative of y(t) = 16 – 4t2 is

Here is a summary of some important derivative rules:

EXERCISES
4.20 Use derivative rules to verify the derivatives we found for each of the functions from the previous exercise set.
a) f(x) = x2 + 3
b) f(x) = x2 + x
c) f(x) = 3x
d) f(x) = 3x + 1
e) f(x) = –2x + 2
f) f(x) = x3 + x
4.21 Find the derivative of each polynomial.
a) f(x) = 9x5 – x4 + 8x3 + 4x + 3
b) x(t) = 2t3 + 7t2 + 6t – 1
c) x(t) = 2.5t3 + 7t2 + 6.3t – 1
d) x(y) = –y4 – 3y3 + 2y2 + 2y – 2
e) h(t) = 9.9t4 – 3.7t3 – 2.2t2 – 1.1 t + 0.2
4.22 The parabola y = x(x – 1) = x2 – x has a single point where the slope is 0. Find the value of x where the slope, i.e., the derivative, is 0. Then find the corresponding y. (The point (x, y) identifies the vertex of the parabola.)
4.23 The function y = x3 – x has two points where the slope is 0. Find both. Sketch the graph of the function by plotting points or using a calculator, and verify that the tangent line looks horizontal at both points.
4.24 Use derivative rules to find an equation of the tangent line to the parabola y = 3 – x2 at the point (1,2). (Hint: you are given a point, and the derivative tells you the slope.)
4.25 A pencil dropped from a height of 4 feet has a height function that looks like y(t) = 4 – 16.1t2. It only takes about 0.49844 seconds (not a full half second) for the pencil to reach the floor.
a) Find the derivative of y(t).
b) Find the slope of the tangent line when t = 0.49844.
c) How fast does the pencil hit the floor?
4.26 A pencil thrown vertically into the air from a height of 4 feet has a height function that looks like y(t) =4 + 5t – 16.1t2.
a) Find the derivative of y(t).
b) Find the slope of the tangent line when t = 0.
c) How fast is the pencil moving when t = 0?
d) At what time t does y′(t) = 0?
e) We know y′(t) = 0 means that the slope of the tangent line is zero. What does it physically mean about the motion of our pencil?