Mathematics for the liberal arts (2013)

Part I. MATHEMATICS IN HISTORY

Chapter 4. CALCULUS

4.8 Slopes and Optimization

In calculus, the term optimization refers to finding the maximum or minimum of some quantity. The maximized quantity can refer to something physical, like the maximum height of a ball thrown into the air. Or it can be non-physical, like the production level of a manufacturing plant that maximizes profit for the company (or minimizes cost).

A Simple Optimization Example

Consider the parabola f(x) = x(x – 2) = x² – 2x in Figure 4.12.

From the graph, it seems obvious that the function has a minimum occurring between x = 0 and x = 2. You may even intuitively guess that the smallest value happens precisely at x = 1. Let’s use calculus to verify this.

Figure 4.12 Finding the minimum of a parabola.

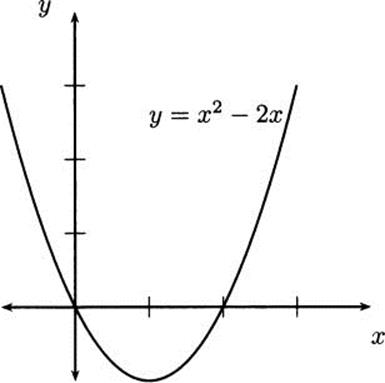
The key to finding a minimum is to consider slopes, which means we want to use the derivative function. For this parabola, the derivative is f′(x) = 2x – 2.

Observation 1: If the derivative is negative, then the slope of the function is “down” and the function gets smaller (or more negative) as we move to the right. A point where the slope is negative is not going to be a minimum because we can move a little bit to the right and find smaller function values.

When is f′(x) = 2x – 2 negative? Compute:

For any value x < 1 we know that the derivative is negative and, consequently, f(x) gets smaller as we move to the right. In mathematical language, we say f(x) is decreasing. No x on the left side of 1 can possibly be a minimum of f. Look at the graph, and see that this makes sense.

Observation 2: If the derivative is positive, then the slope of the function is “up” and the function gets bigger (or less negative) as we move to the right. A point where the slope is positive is not going to be a minimum because we can move a little bit to the left and find smaller function values.

When is f′(x) = 2x – 2 positive? Compute:

For any value x > 1 we see that f(x) gets larger as we move to the right, and smaller as we move to the left. In mathematical language, we say f(x) is increasing. No x on the right side of 1 can possibly be a minimum of f. Look at the graph, and see that this makes sense.

Putting these two observations together, we now can be certain that x = 1 is the location of a minimum of f, for f is decreasing when x < 1 and increasing when x > 1.

The value x = 1 is the location of the minimum. If we were asked to find the minimum value of the function, we would want to put that value back into f to find the y-value. For this parabola, the minimum value would be f(1) = 1²– 2 · 1 = – 1. If we were asked to give the lowest point on the function, we should give the ordered pair for the point, (x, y) = (1, –1).

Critical Points

Given a function f(x), we are interested in places where f may have a maximum or minimum. In general, functions may have no maximum or minimum, or they may have one or two or possibly many maxima and minima. So far, we have discovered that f′(x) > 0 guarantees that x is not the location of a max or min. We also have seen that f′(x) < 0 guarantees that x is not the location of a max or min.

Where then should we look for maxima and minima? Author William Priestley suggests we should think about such problems like Sherlock Holmes.¹ There is a famous Holmes quote that reads, “When you have eliminated the impossible, whatever remains, however improbable, must be the truth.” We have seen that a max or min is impossible where the derivative is either positive or negative. According to Sherlock Holmes, we eliminate these places and look for maxima and minima at the points that remain, i.e., at the places where the derivative is not positive or negative.

Definition. If f(x) is a function, then the critical points of f are the places where f′(x) is not positive or negative. Critical points happen where f′(x) = 0 or where f′(x) is undefined.

Critical points are not always maxima and minima, but if we follow the thinking of Sherlock Holmes they are the right places to look for maxima and minima. In mystery parlance, you might call them suspects. They are the places we suspect to find maxima and minima.

EXAMPLE 4.25

Let . Find any maxima or minima.

Solution: To check for critical points, we take the derivative:

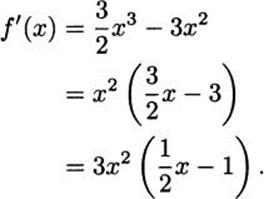
There are two ways a critical point can occur: the derivative can be zero or it can be undefined. In this example, the derivative is a polynomial, so there is no way for it to be undefined (we’ll never divide by zero, take the square root of a negative, etc.).

So we can focus on zeros. This is why we factored the derivative. It makes finding zeros simpler. If we set f′(x) = 0, we can see that either 3x² = 0 or x – 1 = 0. Consider each, in turn. If 3x² = 0, then x = 0. If x – 1 = 0, then x = 2.

So the function f has critical points when x = 0 or when x = 2. Accordingly, these are places to look for maxima and minima. Let’s consult a graph of f (Figure 4.13).

Figure 4.13 Checking the critical points at x = 0 and x = 2.

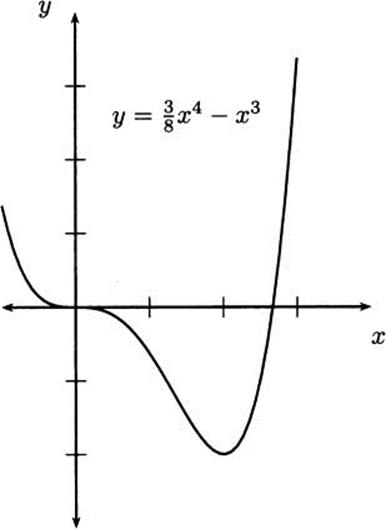
It would appear that x = 2 is the location of a minimum of f, but x = 0 is neither a maximum nor a minimum. When x = 0, the slope of the tangent line momentarily becomes zero (that is, horizontal). It looks like the function decreases on the left side of x = 0, becomes momentarily horizontal, and continues decreasing to the right until it reaches a minimum at x = 2.

We can verify the maxima and minima of a function in practice by checking the function value at a critical point and comparing to function values on both sides. Even without the graph, we could check:

As the graph indicates, the function is a bit positive when x = –0.1 and a bit negative when x = 0.1, telling us that (x, y) = (0,0) is a critical point that is not a max or min. However, when checking around x = 2, we see that the function is larger (that is, less negative) on both sides, verifying that x = 2 is the location of a minimum.

Our conclusion is that the minimum value of f is –2, which occurs at the point (x, y) = (2, –2). There are no maxima.

EXAMPLE 4.26

Find the maxima and minima of f(x) = .

Solution: To check for critical points, we take the derivative. We can either use the chain rule, thinking of f as a composition of functions, or we can first switch to fractional exponents.

Using fractional exponents, a cube root is the same as an exponent of 1/3, so . (Remember that you multiply exponents when taking a power of a power.) So, the derivative is .

Critical points occur where the derivative is not positive and not negative. We need to look for values of x with either f′(x) = 0 or where f′(x) does not exist.

We can readily see that there are no values that make the derivative zero. The function f′ is a fraction, and fractions can only be zero when the numerator (top part) is zero. However, there is one value of x that makes the derivative undefined, x = 0, since we can’t divide by zero. So x = 0 marks a critical point.

We know from the previous example that a critical point may not actually indicate a max or min, so we’ll check the values of the function on each side:

The critical point at x = 0 is apparently a minimum of f, because the values of the function are greater on both sides. Let’s compare with the graph in Figure 4.14.

Figure 4.14 Checking the critical point at x = 0.

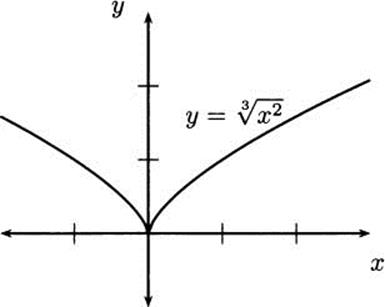
Our graph confirms that x = 0 is the location of a minimum of f. The graph also helps us visualize what occurs. At the origin, the tangent line to f becomes vertical, and you may recall that vertical lines have undefined slope (they are the only lines that cannot be written as y = mx + b, because there is no m).

The sharp point where the derivative becomes undefined is called a cusp, and this cusp forms a minimum for f. The function f has no maximum points.

In summary, optimization problems are solved by computing the derivative. Points where the derivative of a function is positive or negative will not be maxima or minima. If we eliminate these points, the remaining points are called critical points. Critical points occur where the derivative is zero or undefined and may or may not mark maxima and minima. We have to check each critical point in turn to see what kind of point it is.

EXERCISES

4.40 Find the maxima and minima of each function. Compare with a graph to confirm your answers.

a) f(x) = x³ – x

b) f(x) = x² – 2x + 1

c) f(x) = x⁴ – 4x³ + 6x²

d) f(x) = x^1/3

e) f(x) =

f) f(x) = 1/x