Mathematics for the liberal arts (2013)

Part I. MATHEMATICS IN HISTORY

Chapter 4. CALCULUS

4.11 Marginal Revenue, Cost, and Profit

If we are a company that manufactures some item, then the marginal cost of the item is said to be the cost of increasing our production level by one item. For example, if we can produce 10 hand-held radios by spending $33.67 for parts and labor, and 11 radios would cost us $35.77, then we can compute the marginal cost to be $35.77 – $33.67 = $2.10. At a production level of 10 radios, the marginal cost for making one more radio is $2.10.

Perhaps for our particular production line, the cost of making x radios is modeled by the function

We can make a couple of easy observations. One observation is that the cost of making zero radios is C(0) = 7. In most manufacturing situations there are some expenditures even when nothing is produced. These are called fixed costs. We can also verify the marginal cost for producing the eleventh radio by computing C(11) – C(10) ≈ 35.77 – 33.67 = $2.10.

EXAMPLE 4.29

Marginal cost generally depends on the production level, and it is common that the marginal cost decreases as we make more and more items. In fact, you’ve probably heard the phrase “efficiencies of scale.” Verify that the twenty-first item costs less to produce than the eleventh.

Solution: We’ll use the cost function. The cost of the twenty-first item is the difference between the cost for twenty-one items and the cost for twenty items:

The cost for the twenty-first radio is $2.03, which is less than the $2.10 that the eleventh radio costs to produce.

Definition. If C(x) is the cost of producing x items, then the marginal cost function is the derivative of the cost function. That is, MC(x) = C′(x).

EXAMPLE 4.30

Since the cost function for radios is

the marginal cost function is

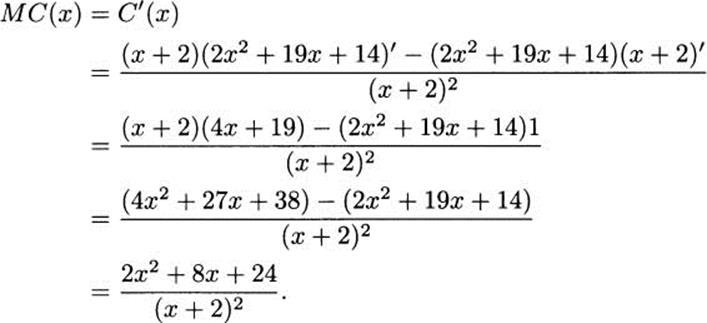
It follows that the marginal cost when producing 10 radios is C′(10) ≈ $2.11, and the marginal cost when producing 20 radios is C′(20) ≈ $2.03.

Notice that we don’t get precisely the same answer when using the derivative as we did by direct computation, but the results are very close. This is because our derivative definition of marginal cost is really a differential approximation of the cost for one more item.

Recall how differential approximation works. For small values of Δx, we know that

or equivalently,

If we take Δx = 1 (we are interested in the change in cost that comes from producing just one more item), we get ΔC ≈ dC/dx. The cost of one more item is approximately the derivative of the cost function. The intuitive definition of marginal cost and the calculus definition are approximations.

Revenue and profit work the same way.

Definition. If R(x) denotes the revenue from producing x items, then the marginal revenue is MR(x) = dR/dx. If P(x) denotes the profit from producing x items, then the marginal profit is MP(x) = dP/dx.

The marginal revenue is approximately the change in revenue that comes from producing one more item, and the marginal profit is approximately the change in profit from one more item.

The marginal profit function is the difference of the marginal revenue and marginal cost functions. That is, MP(x) = MR(x) – MC(x).

This agrees with our intuition. Since profit is revenue minus cost, the profit from one more item should be the revenue for the item after its costs are subtracted.

Proof. The rules of derivatives make this easy to verify:

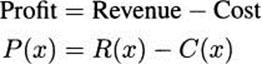
and taking derivatives of both sides,

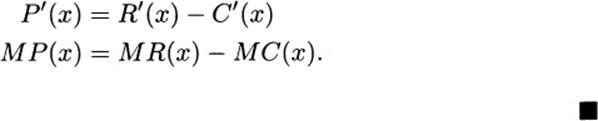
Maximizing Profit

In a business setting, raising revenues is good. Cutting costs is good. But maximizing profit is best, because that is what puts money in our pockets. If our business is modeled by a cost function and a revenue function, can we determine the production level that maximizes our profit?

Recall from the optimization principle (p. 261) that maxima of a function occur at critical points. We will want to check places where the derivative of P(x) is zero or undefined.

In general we need to worry about derivatives being undefined, but this is not a great worry for the profit function P(x). Remember, the derivative tells us the marginal profit, which is approximately the profit for making one more item. It would be an uncommon scenario where the profit for the next item couldn’t be determined. Consequently, we can assume that critical points of the profit function occur because the derivative is zero.

Theorem. Profit maxima (and minima) occur at production levels for which the marginal cost and marginal revenue coincide, that is, at values of x for which MC(x) = MR(x).

Proof. Maxima (and minima) occur at critical points, i.e., where the derivative is zero or undefined. Since there is not a worry that marginal profit is undefined, maxima (and minima) will occur where the derivative is zero. Calculating:

and, adding MC(x) to both sides, it follows that

We can verify this result intuitively with the following thought experiment. Assume we are manufacturing radios and our current production level is x radios.

If the marginal cost, MC(x), is less than the marginal revenue, MR(x), then we should increase our production level by at least one more radio. It will increase our profit (by increasing our revenue more than our costs). On the other hand, if the marginal cost is more than the revenue, i.e., MC(x) > MR(x), we should produce fewer radios. The cost savings will more than make up for the loss in revenue.

So, the maximum profit can only occur where the marginal cost neither lags nor exceeds the marginal revenue.

A similar argument works for minimum profit. The minimum profit will also occur at a production level where the marginal cost and marginal revenue coincide. If we invoke the precept of Sherlock Holmes yet again, we have to remember that places where the marginal cost and marginal revenue coincide are only “suspects” for the maximum profit. We still have to check each one.

EXAMPLE 4.31

Yo-yos sell for $2 each. The cost of producing x yo-yos is C(x) = 50 + 0.01x².

How many yo-yos should be produced to maximize profit?

Solution: Note that we haven’t been given a revenue function, but we have been given enough information to figure it out for ourselves. Since yo-yos sell for $2, if we sell x of them, our revenue function is R(x) = 2x.

To maximize profit, we want to consider when MC(x) = MR(x), so we compute the derivatives, MC(x) = 0.02x and MR(x) = 2. Setting them equal, we learn that

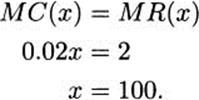
The profit for 100 yo-yos is R(100) – C(100) = 200 – (50 + 100) = $50. This could be a maximum, but it could also be a minimum (or even just a lucky point where the marginal cost and revenue happened to coincide by accident). We can verify that it is a maximum in several ways, but probably the two most obvious checks are:

We could calculate the profit for 99 yo-yos and for 101 yo-yos and discover that in each case the profit is less than $50 (i.e., less than the profit for 100 yo-yos). It is in fact $49.99 at both x = 99 and x = 101.

We could use a computer or calculator to graph the profit function P(x) = 2x – (50 + 0.01x²), on an interval around 100 and see that x = 100 is the location of the highest point.

EXAMPLE 4.32

A plane holds 450 seats. Tickets cost $400 each, and the cost of operating the plane with x passengers is C(x) = –0.001x³ + 0.9x² + 130x + 3000. How full should the plane be to maximize profit?

Solution: As in the previous example, we have to realize that a $400 ticket price implies that the revenue function is R(x) = 400x. To find critical points of the profit function, we take derivatives and set marginal cost and marginal revenue equal.

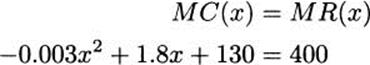
Subtracting 400 from both sides gives

Since this is a quadratic equation we can solve with the quadratic formula to get

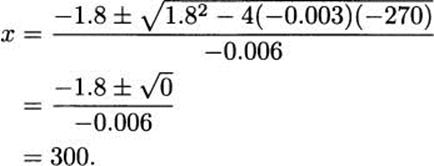
We still need to verify that selling 300 tickets maximizes profit, so we check values on each side:

It looks as though x = 300 is not a maximum. (It is not a minimum either.) Admittedly, the values are very close, so close that we should suspect or at least be cautious about rounding error. Let’s check again, with values a little further from 300:

Indeed, it looks like x = 300 is not a maximum or minimum for profit. That leaves our question unanswered: How many tickets should we sell to maximize profit? The answer is “all of them.”

Here’s how we see that: Since the critical point did not provide an answer, we must look at the boundary, that is, the smallest and largest possible values of x. The fewest number of tickets we can sell is 0, and the most is 450, so this entire problem takes place on the interval [0, 450].

Check the profit at the endpoints of the interval:

The profit for selling 450 seats is $27,375.00, which is greater than the value at x = 0 (which generates a loss) and the value at x = 300 where the critical point occurred. A full plane generates the greatest revenue.

EXERCISES

4.56 Graph the revenue function R(x) and the cost function C(x) for Example 4.31 together on one graph.

a) Sketch the tangent to each curve at the location of the maximum, x = 100, to demonstrate that the slopes of both curves agree there.

b) Draw a vertical line between the two curves at x = 100. The length of this line represents the profit. You should notice that the maximum vertical distance occurs where you’ve drawn the line.

4.57 Graph the revenue function R(x) and the cost function C(x) for Example 4.32 together on one graph.

a) Sketch the tangent to each curve at the location of the maximum, x = 300, to demonstrate that the slopes of both curves agree there.

b) Draw a vertical line between the two curves at x = 300, and another at x = 450. The lengths of these lines represent the profit at each capacity. You should notice that the larger vertical distance occurs at x = 450.

4.58 At a production level of x = 200 items, MC(x) = 7 while MR(x) = 10.

a) To maximize profit, how many items should we produce: fewer than 200, exactly 200, or more than 200 items?

b) Which has greater slope at x = 200: the cost function C(x) or the revenue function R(x)?

4.59 I intend to produce computers that sell for $400 each. My cost for producing x computers is C(x) = 1000 + x²/80.

a) How many computers should I produce to maximize my profit?

b) How much profit will I make?

4.60 Assume that the price I can charge for a product drops if I flood the market with items, so that the price I can charge is p(x) = 2000/x.

a) What is the revenue generated by x items, R(x)?

b) What is the marginal revenue function, MR(x)?

c) Assume that the cost function is an increasing function. Does that mean that the marginal cost function, MC(x), is less than 0, exactly 0, or greater than 0?

d) Assuming that I produce at least 1 item, prove that the maximum profit occurs when x = 1.