Mathematics for the liberal arts (2013)

Part I. MATHEMATICS IN HISTORY

Chapter 4. CALCULUS

4.12 Exponential Growth

Since derivatives tell us rates of change, it should be little surprise that calculus is important for the study of different kinds of growth. For example, linear growth (which describes something whose size looks like a line when you graph it over time) is very easy to describe with calculus. Its derivative is a constant (the slope of the line).

One of the most important kinds of growth is exponential growth. It describes many biology situations, such as the growth of a bacteria colony or the spread of a disease. It has a role in computing physical properties such as the decay of radioactive elements, or changes in temperature. It also has applications to finance.

Simple and Compound Interest

If you invest a sum, say $1000, and you receive simple interest at a rate of 5%, then each year you are paid 5% of your $1000 as interest. Over time, your investment will grow as in the following table:

No matter how many years you maintain your investment, the principal will always be $1000, and the interest payment will be 5% of that $1000. This kind of arrangement is typical for a bond that makes regular payments to you.

If we write r for the fractional interest rate (i.e., r = 0.05 denotes a 5% rate), and P for the principal invested, then over time the investment is worth

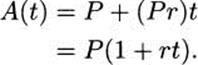
With an investment that pays compound interest, each interest payment is added to the principal. If you invest $1000, earning 5% annually, your principal becomes $1050 after the first year. Consequently the second year’s interest payment will be larger, because it will be calculated based on both the original $1000 investment and the previously awarded interest—5% of the entire $1050. Over time, your compounded investment will grow like:

Determining a formula for your investment after t years is a little harder than for simple interest, but not too bad if you write things down the right way. After 1 year, your balance is

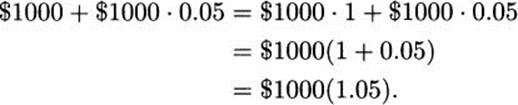
In the second year another interest payment is added, 5% of the new amount, increasing your balance to

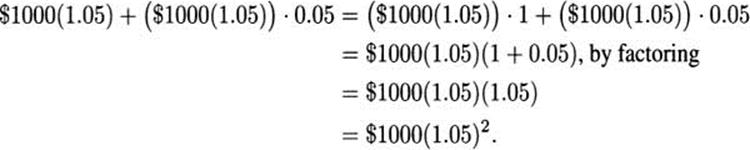
Each year, the new balance is derived from the previous balance by multiplying by 1.05, and the amount after t years is

Again, let r denote the fractional interest rate. If P is the original principal invested and t is years, then the amount the investment is worth after t years (compounded every year) is

A Review of Exponentials and Logarithms

Since compound interest is a kind of exponential growth, we take a moment and review some of what we learned from algebra class about exponential functions and their inverse functions, logarithms.

Definition. Let a be any positive real number, and define f(x) = a^x. Then f is said to be an exponential function with base a. If a > 1, then f is an exponential growth function, and if 0 < a < 1, then f is an exponential decayfunction.

EXAMPLE 4.33

The function f(t) = 1.05^t is an exponential growth function. The function g(t) = 0.95^t is an exponential decay function. Some sample values of each are computed in the following tables.

The exponent of an exponential can be any real number, though if it is not an integer we will usually use a calculator or a computer to aid with the calculation. On scientific calculators, the button for computing general exponentials is usually marked with a caret ^ or the expression y^x, and it can compute values such as 1.05^3.3 = 1.17469 and 0.95^10.4 = 0.58658 (these are approximate values).

You may also recall from algebra class that we have identity laws for exponentials. We summarize some here:

We can readily verify these with a calculator. For example, if a = 1.3, b = 5.5, and x = 3, then

while

We get the same answer either way.

There is one special base that is so important that we reserve a letter for it, and that is the number e = 2.71828182845904523536…. Like π, e has a nonterminating, nonrepeating decimal expansion. Scientific calculators have a key that is usually marked either exp or with the expression e^x which calculates exponentials with base e. With your calculator, you can verify a few values of this function.

Figure 4.22 The natural exponential function f(x) = e^x.

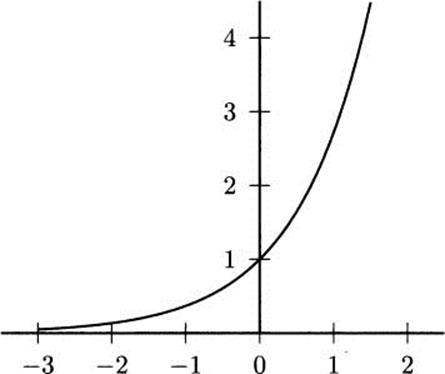
If you inspect the graph of the exponential function in Figure 4.22, you will see that it passes a horizontal line test (horizontal lines intersect the graph in a single point). You may remember from algebra class that functions that pass the horizontal line test have inverse functions. The inverse of the exponential with base a is called the logarithm with base a, and it is sometimes written as g(x) = log_a x.

Inverse functions “undo” each other, just as f(x) = and g(x) = x² undo each other. For example, start with x = 9. Then f(9) = = 3, and the reverse process that takes us from 3 back to 9 is g(3) = 3² = 9.

For the calculus student, the most important logarithm function is the logarithm with base e, which is called the natural logarithm, since it is the inverse to the natural exponential function. The notation for the natural logarithm is g(x) = ln x. Scientific calculators have a key labeled ln that computes natural logarithms, not to be confused with the log key which computes common (base 10) logarithms.

Using a calculator, we can verify the inverse relationship of the natural exponential and natural logarithm functions. First, compute e^1.5 = 4.4817. Then check that ln(4.4817) = 1.5. It works the other way too, that is, computing the logarithm first and then doing the exponential. For example, compute that ln(10) = 2.3026 and verify that e^2.3026 = 10.0.

Figure 4.23 The natural logarithm function f(x) = ln x.

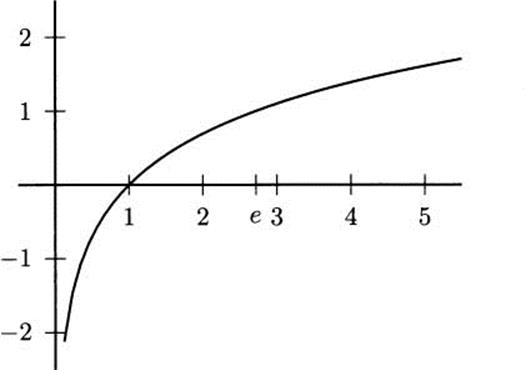
Some values of the natural logarithm are given in the table below. You may wish to check that you can produce them with your calculator. Notice that they agree with the graph of the natural logarithm in Figure 4.23.

Some computer programs use log(x) to denote the natural logarithm. If you suspect this, you can check by computing log(10). If you get an answer of 2.302585, then it is the natural logarithm. The common logarithm would return 1.0.

As with exponentials, there are identity laws for logarithms that help us with computations. Versions of these work with logarithms of any base, but we focus on the natural logarithm.

EXAMPLE 4.34

If I invest $1000 and receive 5% interest compounded annually, how long will it be before I have $5000?

Solution: We computed previously that the amount of money after t years is

We need to find the value of t when A(t) = $5000. Solving,

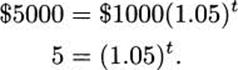
Here, we can take the logarithm of both sides.

Apply the identity for log of a power to the right-hand side.

Now get t alone on one side.

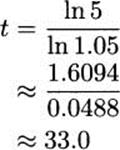
It takes about 33 years for this $1000 to grow to $5000.

Derivatives of Exponentials and Logarithms

We saw that $1000 invested at a simple interest rate of 5% has a value over time of A(t) = P(1 + rt) = 1000(1 + .05t) = 1000 + 50t. What happens if we take the derivative of this function?

The answer is A′(t) = 50. Does this represent anything useful? It does indeed, and recalling the differential notation can make it a bit more apparent. We could just as correctly have written,

The derivative tells us the (instantaneous) rate of change of the amount over the time. Consider the units that apply here. A change in A, which we write as ΔA is measured in dollars. A change in t is measured in years. The fraction dA/dt is the (instantaneous) slope of the function, measured in dollars/year. It tells us how fast our money is growing at any moment, at a rate of 50 dollars/year.

We don’t yet have a formula for the derivative of an exponential function, such as A(t) = 1000(1.05)^t. It is tempting to try to apply the power rule, but that is a mistake. A power, like x², is not an exponential, like 2^x. A different rule applies.

It turns out that the slope of an exponential function is always proportional to the height of the function at the point of tangency (i.e., there is some constant number that you multiply the value of the function by to get the slope). We get a sense of this if we remember that

If we take Δt = 1, then ΔA is the amount an investment will grow over the period of 1 year, and that amount is the interest rate times the current amount. If A(t) = 2000 for some t and r = 0.05, then we know that

This is an approximation of the slope, but for the derivative we want the exact slope. To discover this, we’ll take a detour and look at the natural exponential function, e^x.

You may wonder what is so ‘natural’ about the natural exponential function. It is natural because it has a simple differentiation formula.

The natural exponential rule: The derivative of f(x) = e^x is f′(x) = e^x. The natural exponential function is its own derivative.

Figure 4.24 The natural exponential function is its own derivative.

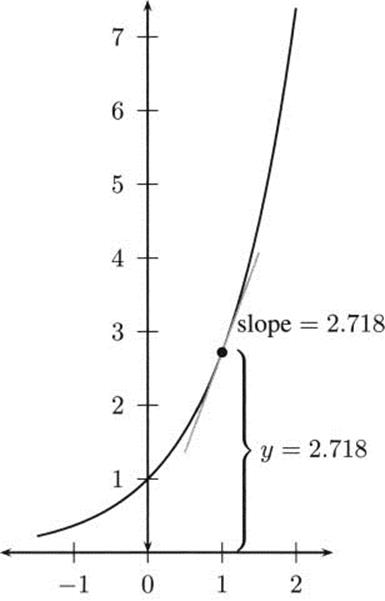
At any point on the graph of y = e^x, you’ll find the slope of the tangent line is the same as the height of the graph. Check, for example, by sketching a tangent at the point (0,1), and notice that your line has slope 1 (it extends up at a 45 degree angle). In Figure 4.24 the tangent at the point (1, e) has slope e, as we expect.

The natural exponential is the only exponential equal to its derivative. The derivative of any other exponential function contains an extra constant.

The general exponential rule: If a > 0 is any real number, then the derivative of f(x) = a^x is f′(x) = a^x ln a.

EXAMPLE 4.35

Find the derivative of A(t) = 1000(1.05)^t.

Solution: By the general exponential rule,

As promised, the derivative is proportional to the function A(t). That is,

and the constant of proportionality is ln 1.05 ≈ 0.04879. Also note that 0.04879 is approximately the same as the interest rate of 0.05. Of course, 0.05 appears in the derivative estimate we would get from using Δt = 1, i.e., if we computed A′(t) ≈ A(t + 1) – A(t) = 1000(1.05)^t+1 – 1000(1.05)^t = 1000(1.05)^t(0.05).

EXAMPLE 4.36

What is the slope of the tangent to A(t) = 2000(1.07)^t, when t = 0? What about when t = 3?

Solution: The derivative of A is A′(t) = 1000(1.07)^t ln 1.07, so the slope when t = 0 is A′(0) = 1000(1.07)⁰ ln 1.07 = 1000 ln 1.07 ≈ 67.66. The slope when t = 3 is A′(3) = 1000(1.07)³ ln 1.07 ≈ 82.88.

Like the natural exponential function, the natural logarithm function has a nice derivative.

The natural logarithm rule: The derivative of f(x) = ln x is f′(x) = 1/x.

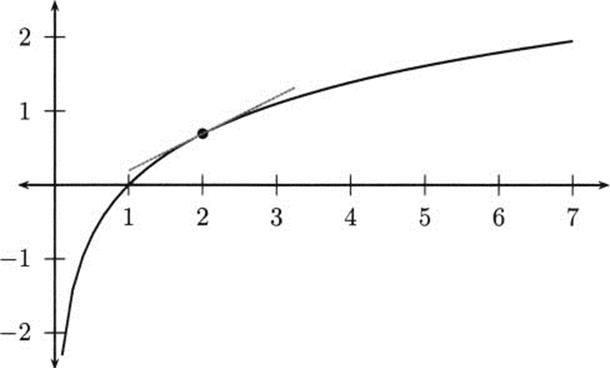
Figure 4.25 shows a graph of y = ln x together with a tangent line at x = 2. Notice that the slope appears to be 1/2, as the natural logarithm rule states. Ask yourself, what should the slope be when x = 1? Does the graph look right to you at that point?

The natural logarithm rule “fills in” a hole that we had in our differentiation rules. For each power, f(x) = xⁿ there is a function that we can take the derivative of to get f, except in the case where n = – 1. For example, , and . In general, , as long as n ≠ –1. So, until we learned the derivative of the logarithm, we did not have a function whose derivative was x^–1 = 1/x.

Figure 4.25 The derivative of ln x is 1/x.

EXAMPLE 4.37

The number of computer clock cycles a particular computer program needs to sort n items of data is given by the formula T(n) = 7000 + 1440n ln(n). For example, sorting n = 2000 data items requires about T(2000) ≈ 21.9 million clock cycles. At what rate is the sort time changing when n = 2000?

Solution: Since we are asked for a rate, we know that the answer is a derivative. It is reasonable to ask “what is the variable?” and “what is the function?” In this case, the variable is n, the number of items we wish to sort. The function is T, the time required to sort n items.

The rate we want is then the change in T with respect to n, or . Using the sum and constant coefficient rules we have

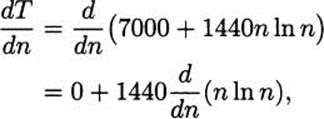
and applying the product rule and natural logarithm rule yields

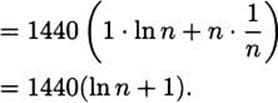
If we evaluate at n = 2000 we get 1440(8.6) ≈ 12,385 cycles/item. The computer program requires approximately 12,385 cycles to accommodate another sort item.

To check, let’s compute directly the difference between sorting n = 2001 items and n = 2000 items (without calculus).

This agrees well with our derivative calculation. ?

EXERCISES

4.61 If I invest $ 1500 and receive a return of 6% simple interest for two years, how much money will I have?

4.62 If I invest $5000 and receive a return of 8% simple interest,

a) How much interest will I receive each year?

b) How many years will be required to receive $45,000 of interest?

4.63 If I invest $5000 and receive a return of 8% compounded annually, how many years will it take to grow to $50,000?

4.64 The “rule of 72” says that if you receive a compound annual interest rate of p%, then the number of years it takes for your money to double is 72/p years. So, a 6% return will double your money in approximately 72/6 = 12 years.

a) Compute the number of years it takes $100 to double to $200 at an annual compound rate of 6% and compare it to the rule of 72.

b) Compute the number of years it takes $100 to double to $200 at an annual compound rate of 3% and compare it to the rule of 72.

c) Compute the number of years it takes $100 to double to $200 at an annual compound rate of 12% and compare it to the rule of 72.

4.65 Every exponential function f(t) = A · b^t can be rewritten using the natural exponential function in the form f(t) = Pe^rt. Find suitable P and r so that 1000(1.05)^t = Pe^rt by applying these steps:

a) Let t = 0 to find P.

b) Using P from part (a), let t = 1 and solve for r.

c) Write f(t) using the natural exponential.

4.66 If we invest $1000 at a 6% interest rate compounded monthly, then the balance after t years is 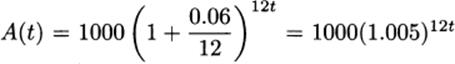. Find suitable P and r so that 1000(1.005)^12t = Pe^rt.

4.67 Compute the derivative of each function.

a) f(t) = te^t

b) A(t) = 100e–^t.

c) A(t) = e^–1.8t

d) g(x) = (ln x)e^x

e) y(t) = t(ln t – 1)

f) h(x) =

g) f(x) = ln(3x)

h) f(x) = 2 ln(3x + 4)

4.68 Find the equation for the tangent line to y = e^x at the value x = 1, as illustrated in Figure 4.24.

4.69 Find the equation for the tangent line to y = ln x at the value x = 2, as in Figure 4.25.

4.70 During the Cold War, nuclear detonators were made from radioactive Polonium-210. Because it is highly radioactive, Polonium-210 quickly decays into other elements. If a detonator initially contains 11 mg of Polonium-210, then the amount (in mg) remaining after t days is A(t) = 11e^–0.00502t.

a) How much Polonium-210 remains after 138 days? What can you conclude about the half-life of Polonium-210?

b) At what rate (in mg/day) is the Polonium-210 decaying into other elements when the detonator is new?

c) At what rate (in mg/day) is the Polonium-210 decaying into other elements when the detonator is 180 days old?