Mathematics for the liberal arts (2013)

Part I. MATHEMATICS IN HISTORY

Chapter 1. THE ANCIENT ROOTS OF MATHEMATICS

1.2 Ancient Mesopotamia and Egypt

The Middle East.¹

Two of the earliest civilizations arose in the Near East.

Ancient Mesopotamian history. All dates are BCE.

Mesopotamia (from the Greek, literally “between the rivers”) is the plain between the Tigris and Euphrates rivers, about 600 miles long, in modern-day Iraq. Mesopotamia was home to the earliest known agriculture. The major crops were wheat and barley, but there were also fruits, including dates, grapes, figs, melons, and apples; vegetables, including eggplant, onions, radishes, beans, and lettuce; and sheep, cattle, goats, and pigs.

Figure 1.1 The Tigris and Euphrates rivers are above and to the left of center; the Nile is on the left.¹

Between the Rivers

The farmers relied on the flooding of the Tigris and Euphrates. These floods, which could be violent and destructive, nonetheless left behind very fertile silt. Mesopotamia doesn’t get much rain, so the other important ingredient to agriculture was irrigation. One of the critical functions of the government was the construction and maintenance of irrigation systems. The first Mesopotamian civilization was the Sumerian, named after the city-state of Sumer in southern Mesopotamia. It arose circa 3500–3000 BCE. Politically, the early Sumerians did not have an empire; empires came later. Instead, they were organized into city-states, ruled by priest-kings. These city-states built up bureaucracies to manage the irrigation systems and the surplus grains. They even had postal systems. The Sumerians are credited with the invention of plows, the potter’s wheel, and wheeled carts. Their greatest invention was an improved writing system. Earlier writing systems had relied principally on pictograms, symbols which were meant to look like the thing represented. The Sumerians developed, over many hundreds of years, a system of standardized ideograms, symbols that represented ideas.

The Sumerians, and their successors in Mesopotamia, wrote by using a stylus, a reed cut at an angle, to make impressions in wet clay tablets. The tablets were then baked until hard. Their writing is called cuneiform, from the Latin cuneus (wedge) and forma (shape). It is from these tablets that we learn most of what we know about their history. Ironically, the preservation of this history was often assisted when the buildings housing the tablets were burned. This baked the tablets, making them more durable.

Mesopotamia is a crossroads. This allowed it to be a trading center and to profit from the ideas of other civilizations. It also was subject to regular raids and occasional full-scale invasions from its neighbors. So there was a succession of civilizations and empires through the years. The Sumerians were conquered by the Akkadians, whose most famous ruler was Sargon the Great, who lived around 2250 BCE. The Akkadians were replaced by the Babylonians.

The most important Babylonian king was Hammurabi, who ruled c. 1792–1750 BCE. He is famous for promulgating the first code of laws, a list of 282 short “laws.” Here is one: “If a man puts out the eye of an equal, his eye shall be put out.” Presumably he can put out the eye of an inferior with impunity. A “tooth for a tooth” is also here. Many of the laws end with “shall be put to death.”

If you read about ancient Mesopotamia, you will often find it referred to as Babylon, even during those times when Babylon was not its most important city. Perhaps this reflects Babylonian cultural accomplishments. In particular, the high point of Mesopotamian mathematics was during this time. After the Babylonians, mathematics was mainly stagnant.

The Babylonians in their turn fell to the Kassites, who had a new weapon, horse-drawn chariots, the tanks of their day. In the 9th century BCE, the Assyrians ruled, relying on iron weapons. In the 7th century came the Chaldean empire, when Nebuchadnezzar built the hanging gardens of Babylon and sent many Hebrews into Babylonian exile. The Persians under Cyrus invaded in 538 BCE, and Alexander the Great took over in 330 BCE, bringing Greek culture with him.

Most of the invaders did not displace the local culture. Instead they adopted much of it. In particular, the bureaucracy essential to managing their conquests tended to stay in place. This bureaucracy included the scribes who were at the heart of mathematics. Early on, the Sumerians developed scribal schools, which taught writing and mathematics, among other subjects, to future bureaucrats. Most of these scribes came from wealthy families. They were the ruling elite of their day.

The schools for scribes became centers of culture, including mathematics. Their main emphasis, however, was business and administration. Irrigation systems had to be run, laws administered, lands apportioned, taxes levied. A very important responsibility, and one that had a profound influence on mathematics in Mesopotamia and elsewhere, was maintenance of the calendar, which required accurate measurements of the heavens.

Most of the tablets from which we learn about Mesopotamian mathematics were created at the schools, for the purpose of training scribes. They usually took the form of solving problems. The problems were stated in practical terms: measuring fields, apportioning inheritance, and so on. But the purpose of the tablets was to train students in mathematical methods rather than in practical problem-solving. In some ways, mathematical textbooks haven’t changed.

Although the tablets reveal a strong mathematical tradition, they do not reveal a lot of theory, or even general methods. These methods are implied by the results, but apparently were restricted to an oral tradition. Sometimes historians have been able to infer the methods used, sometimes they have to guess them.

Numeration One of the greatest accomplishments of the Mesopotamian culture was the development of the best number system of antiquity.

A problem that any sophisticated number system must address is how to group numbers. Small numbers may be expressed by simple ticks, but if we are to handle larger numbers, they must somehow be grouped together. The Sumerians were the first to establish a consistent grouping system. Unlike our number system, which groups by powers of 10 (1, 10, 100, …), the Sumerians grouped by powers of 60 (1, 60, 3600, …). This system is called sexagesimal (from the Latin sexagesimus, sixtieth), as opposed to our decimal system (from decimus, tenth).

No one knows exactly why they chose this system, but one of its useful features is that 60 has many divisors: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, and 60. By contrast, 10 has only four divisors. More divisors make fractions easier to work with. Consider the multiplication 1/2 × 3/5. One way of doing this is to convert to a decimal representation: .5 × .6 = .3. Thus, we can use our regular multiplication and not have to deal with fractions as ratios. It only works, however, because 2 and 5 are divisors of 10. Consider 2/3 × 11/12. This problem does not lend itself to an easy decimal representation in base 10. Ten doesn’t have enough factors. We will see below how a sexagesimal system can handle this multiplication.

The legacy of the Mesopotamian sexagesimal system survives to this day: we divide hours into 60 minutes, minutes into 60 seconds, and we divide the circle into 360 degrees.

One of the most important advances in representing numbers was the idea of place-value notation, developed by the Babylonians. To understand this, let us look at how we represent numbers in our own place-value system. Consider the number 235:

The meaning of each digit depends on its place in the number. So, for example, 235 is not the same as 253.

Since the Babylonians had a sexagesimal system, they would represent the number 235 in powers of 60. Thus

so we might write this as 3,55, using a comma to separate powers of 60.

What number would 3,40,6 represent?

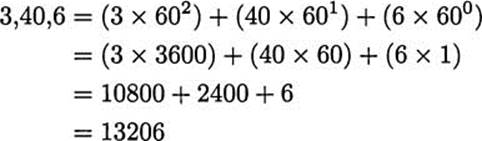
One of the advantages of a place-value system is the ability it gives us to express arbitrarily large numbers with a small set of symbols, ten symbols in the case of our decimal system. The number symbols used in Mesopotamia changed dramatically through the years. The Sumerians used hundreds of symbols, both pictorial and phonetic. Their successors, the Akkadians, developed a standardized system of number ideograms. These ideograms represented the idea of a number, divorcing it from concrete notions such as a “hand,” for five.

The Babylonians reduced the number of symbols to two, one for 1 and one for 10. They repeated these symbols as necessary to get the numbers from 1 to 59, as in Figure 1.2. For numbers greater than 59, they used their place value system, as we do for numbers greater than 9. Figure 1.3 shows how they would write the number 2,34 = 2 × 60 + 34.

Figure 1.2 Babylonian symbols.

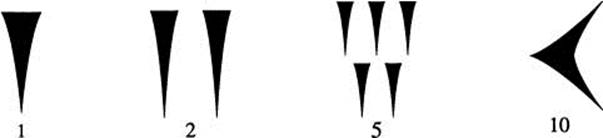
Figure 1.3 Babylonian 2,34.

This system could also handle numbers less than one, in the same way as our decimal system. We write 2/5 as .4. If we use a semi-colon, instead of a decimal point, the Babylonians could use; 24 for two-fifths, since 24 is two-fifths of 60. Since 60 has so many divisors, this was a convenient way of writing fractions. Another example: since 20 is one-third of 60, we would write 1/3 = ;20. Here is an example of a mixed fraction.

The Babylonians did not use a semi-colon, or any indicator of where fractions started, so there was an ambiguity to their numerals. For example, they wrote all these numbers the same way:

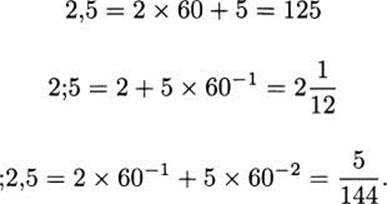
They would determine which number was meant by the context.

The other missing element in this system was the notion of zero. The Babylonians did not have a zero number, and would never write a number such as 2,5,0. They wrote 2,5 and interpreted it as 2,5,0 from context. They did have to develop some way to indicate skipped digits, such as what we mean when we write 0 in the middle of a number, as in 205. This gap was indicated in different ways, often with just a space.

Computation and Algebra The Babylonian number system allowed for a sophisticated arithmetic. Like us, the Babylonians wrote down multiplication tables. They also had tables of squares and cubes of numbers. For division, they used tables of reciprocals. For example, consider the problem 32 ÷ 25. If we had a table giving us .04 as the reciprocal of 25, we could translate the division problem into its equivalent multiplication problem, 32 × .04. This the Babylonians regularly did, aided by the fact that 60 has many divisors. Of course, this works well only when the reciprocal has a nice form; think of trying it with 32 ÷ 7. The Babylonian reciprocal tables were usually restricted to the nicer reciprocals. For other divisions, approximation techniques were used.

The Babylonians were very good at calculating square roots. A tablet from around 1600 BCE gives the approximation = 1; 24, 51, 10. In decimal terms, this is about 1.414213, while the correct value starts 1.414214. … The approximation is within one-millionth of the correct value.

The method they used to obtain such accuracy is not known with certainty, but may be what later was called Heron’s method, since Heron was the first to write it down, over 1500 years later. This method can be used to find the square root of any number N. You start with any guess for , say, x₁. You then generate a sequence of numbers x₂, x₃, x₄, …, as follows.

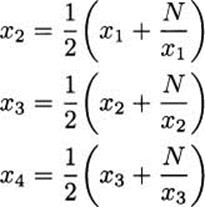
You can continue this pattern as long as you like. The numbers x₁, x₂, x₃, x₄, … get closer and closer to .

As an example, we will approximate . We first guess x₁ = 1.5. (The initial guess doesn’t have to be too accurate. Just pick something reasonable.) Then

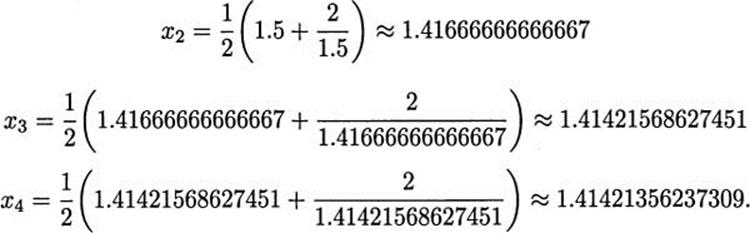
Already, all the digits given for x₄ are accurate.

Babylonian mathematicians had a good understanding of linear equations in one variable, ax + b = c, even though the scribes had no general notion of a variable. They could also solve systems of two linear equations in two unknowns.

Many of the tablets concern problems that involve solving quadratic equations, equations we would write as ax² + bx + c = 0. Here is an example: “I summed the areas of my two square-sides so that it was 0;21,40. A square-side exceeds the (other) square-side by 0;10.”

Let us translate that into modem notation. The number 0; 21, 40 refers to 21/60 + 40/3600 = (21 × 60 + 40)/3600 = 13/36. Also, 0;10 is 10/60, or 1/6. So we have two squares, one of side x, say, and the other of side x – 1/6. Since the sum of their areas is 13/36, the problem is to solve the equation

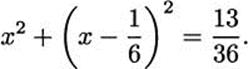
The solution is then given step-by-step. It starts like this: “You break off half of 0; 21, 40 and you write down 0; 10, 50.”

Note that the problem itself is stated in geometric form. This was typical; there was no clear distinction between algebra and geometry. The Babylonians did not have an algebraic notation. They also had no symbols for arithmetic operations, like +, –, ×, ÷. The problems were stated in words.

The solution of the problem is given by a set of specific instructions on how to proceed. This also was typical. There was no notion of a general solution like our quadratic equation, even though the scribes clearly had methods for solving many such equations. The idea of a general theory had yet to be developed.

Given these restrictions, their accomplishments in algebra were impressive.

Geometry The people of Mesopotamia dealt with many practical problems requiring geometric knowledge for their solutions. Surveyors had to measure distance and compute areas. Builders of large structures needed knowledge of distance, area, and volume.

Surviving tablets give us some insight into their geometry. The scribes had mles for computing the areas of triangles, rectangles, and various other plane figures such as pentagons, hexagons, and trapezoids. Rules for computing with circles usually have π = 3, although the better approximation of was also used. The Babylonians had the correct formula for the volume of a truncated pyramid, which is a pyramid with its top cut off.

What we now call the Pythagorean Theorem, a² + b² = c², where a and b are the legs of a right triangle and c its hypotenuse, was known in Mesopotamia at least 1000 years before Pythagoras. A famous clay tablet from the Old Babylonian Period lists a number of Pythagorean triples, which are sets of three numbers obeying the Pythagorean equation, for example, 3–4–5 (since 3² + 4² = 5²). See Section 5.11 for more on these triples.

We must remind ourselves when dealing with cultures several thousand years in the past, that our knowledge is spotty. In the matter of geometry, it has been suggested that clay tablets were not the best medium for drawings. Perhaps the scribes did their best work drawing in sand, or some other medium which has been lost. Having said that, it is certain that their geometry never approached anything like the sophistication attained in ancient Greece. The existing tablets address particular problems, not general theory. There is no notion of proof.

Egypt before Alexander

Ancient Egyptian history. All dates are BCE.

Gift of the Nile Egypt consists of a desert cut by the Nile River. The upper Nile, about 600 miles from Aswan to Memphis, is a narrow valley, not more than 15 miles wide, bordered by cliffs. The lower Nile, about 150 miles from Memphis to the Mediterranean, is a fan-shaped marshy delta. Outside the river valley is only desert.

In ancient times, before modem flood control systems, the Nile flooded every year. The flood left behind rich soil. About 7000 years ago, the Egyptians began to farm this soil. As in Mesopotamia, there was little rain, so the agriculture that developed was reliant on irrigation. Egyptians raised wheat and barley and a variety of vegetables for food, and flax for clothing. The most important domesticated animals were cattle, but they also kept sheep, goats, and pigs. It was one of the most productive agricultural areas in the world, producing in good years a large surplus that could support a sophisticated civilization.

The Egyptians had a written language by about 3200 BCE, almost as early as in Mesopotamia. The hieroglyphs, from the Greek for “sacred carvings,” were pictographs. A little later, the Egyptians developed the cursive hieraticscript, and, in the first millennium BCE, an alphabetic system called demotic.

Hieroglyphs were painted or carved on monuments, while the hieratic and demotic systems were written using ink on papyrus. Papyrus was a type of paper made from a reed, Cyperus papyrus, found in the Nile Delta. Our word “paper” derives from papyrus. Papyrus sheets were cheaper than the clay tablets used in Mesopotamia, but they don’t last as long. Thus much of what we know of Egyptian mathematics, with some exceptions noted below, comes from inscriptions on monuments.

One meaning of hieroglyphic in English is “hard to decipher,” and Egyptian hieroglyphs were unreadable by modem scholars until the decipherment of the famous Rosetta Stone. This stele (inscribed stone slab) was found by Napoleon’s armies in Egypt in 1799. It had a message written in Greek, hieroglyphic, and demotic, which allowed Jean Champollion, after much work, to decipher it in 1821.

Egypt was first brought together under a single ruler about 3100 BCE. In the Old Kingdom (c. 3000–2200 BCE), the Egyptians adopted much from the Sumerians, including irrigation systems, the plow, and metallurgy. They too had a class of scribes to assist in administration, and again it was from this class that most of their mathematics originated. It was during the Old Kingdom that the biggest pyramids were built, including the famous Great Pyramid of Giza (c. 2500 BCE).

Egypt was not organized into city-states like Mesopotamia, but instead was centrally ruled by the pharaoh, who was considered a god. Only under such a centralized system could monuments such as the pyramids be constructed. According to the Greek historian Herodotus (c. 484–425 BCE), who first called Egypt the “gift of the Nile,” the Great Pyramid required the labor of 400,000 men at a time, for three months of the year, over twenty years. That was after the effort of ten years building the road needed to transport the materials. (Herodotus wrote 2000 years after the fact, so the precise numbers shouldn’t be taken too seriously. Nonetheless, they are not far from modem estimates.)

A period of political unrest followed the Old Kingdom, until the arrival of the Middle Kingdom (c. 2100–1800 BCE). Egyptian culture flourished in this period. In fact, it was the high point of ancient Egyptian mathematics. The Middle Kingdom ended with the invasion of the Hyksos, from Syria-Palestine.

The Hyksos were expelled, starting the New Kingdom (c. 1600–1100 BCE). In this period, Egypt expanded its power into the Middle East (Palestine and Syria) and to the south (Nubia and the Sudan). The New Kingdom was followed by a period of weak kings and a number of invasions, including conquests by the Assyrians in 671 BCE, the Persians in 525 BCE, and finally, in 332 BCE, Alexander the Great.

Mathematics in ancient Egypt was applied to many of the same uses as in Mesopotamia: building irrigation systems and granaries, levying taxes, paying workers, and apportioning the surplus grain. Of particular note is surveying. Farms had to be marked off again after each yearly flood destroyed the previous year’s boundaries. For this, surveyors needed geometry—from the Greek geo, Earth, and metria, measure.

As mentioned above, most of what we know about ancient Egypt is from the thousands of inscriptions on monuments they left behind. The most important sources for the later mathematics are, however, a dozen or so papyri. Two stand out. The Moscow Mathematical Papyrus (which is in the Moscow Museum of Fine Arts), dating from about 1850 BCE, contains a list of twenty-five problems. Eleven of these twenty-five concern ways of making different beers and breads. The Rhind Mathematical Papyrus (bought in the 19th century in Luxor, Egypt by a man named Rhind) is a scroll 13 inches wide and 18 feet long, which contains eighty-seven problems and tables. It dates from around 1650 BCE, but its author writes that he copied it from a work written 200 years before that.

Numeration and Arithmetic The Egyptians had one system of numeration for each of their three writing systems: hieroglyphic, hieratic, and demotic. All of them were decimal, that is, they grouped numbers by powers of ten. The hieroglyphic system had symbols for 1, 10, 100, etc. Multiples of these were represented by repeating symbols. The hieratic and demotic systems added symbols for 2, 3, …, 9 and 20, 30, …, 90, and so on, which made writing large numbers much easier. Unlike the Mesopotamians, the Egyptians never developed a fully positional system.

Addition and subtraction in these systems was rather like in our own. For multiplication, they used a doubling system called duplation. It is similar to how modem computers multiply. Here is an example, computing 11 · 17. First we write powers of 2, with their corresponding multiples of 17. Each line is obtained by multiplying the previous line by 2.

Why only four lines? Because we can write 11 = 1 + 2 + 8. Therefore 11 · 17 = (l + 2 + 8) · 17 = 1 · 17 + 2 · 17 + 8 · 17. To complete the multiplication, we need only add the entries in the right-hand column corresponding to 1, 2, and 8, to get 11 · 17 = 17 + 34 + 136 = 187. Division was handled using the same idea, although it was a bit more complicated due to remainders.

Egyptians didn’t use fractions as we do. They only used unit fractions of the form 1/n, for example, 1/2, 1/3, or 1/4. The sole exception is their use of 2/3. Other fractions were expressed as sums of unit fractions. A famous problem from the Rhind Papyrus asks how to divide six loaves of bread among ten men. The answer given was 1/2 + 1/10. You can check that this equals 6/10. In fact, dividing the loaves is easy using 1/2 + 1/10. Cut five of the loaves in half, giving one-half to each man. Then cut the last loaf into tenths, giving each man one tenth. Each man ends up with one-half plus one-tenth.

The Egyptians did not prove that any fraction can be written as the sum of distinct unit fractions (they didn’t have the notion of proof), but it can be proven. To do the actual computations, they used extensive tables. The Rhind Papyrus, for example, includes a table decomposing fractions of the form 2/n into sums of unit fractions.

Geometry One area where Egyptian mathematics excelled was geometry. They knew how to compute areas of rectangles, triangles, and trapezoids, as well as volumes of rectangular boxes and various cylinders. They also used similar triangles. Two triangles are similar if they have the same three interior angles. One triangle is a blown up version of the other. They are useful because the ratios of their corresponding sides are the same. As for circles, again we refer to the Rhind Papyrus, where the area of a circle is given as (8d/9)², where d is the diameter of the circle. This was equivalent to approximating π by 256/81, about 3.16.

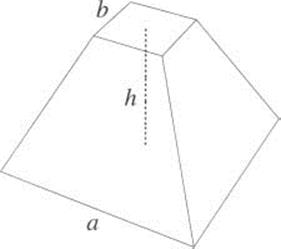
Given the importance of pyramids to them, it is no surprise that the Egyptians knew how to compute the volume of a pyramid. The Moscow Papyrus has a method for calculating the volume of a truncated pyramid. (You can see a drawing of a truncated pyramid on the back of a U.S. dollar bill, underneath an eye.) The method is equivalent to the formula

where α is the length of the lower base, b is the length of the upper base, and h is the height (see Figure 1.4).

Figure 1.4 A truncated pyramid.

The Egyptians did not pursue theoretical geometry the way the Greeks later did. They were, however, unsurpassed in practical geometry. This can be seen in their monuments. The base of the Great Pyramid is an almost perfect square about 756 feet per side. The length of the sides differ by less than one foot—and this was done using 2.5 ton stone blocks (more than 2,300,000 of them). Later Egyptian construction never reached this level of precision.

Algebra The Egyptians were able to solve linear equations, and some quadratic equations. They, as all ancients, were hampered by the lack of a good notation. For them, all problems were word problems.

One method the Egyptians scribes used is called the method of false position. This method was adopted by many other peoples, and used as late as the Middle Ages in Europe. As an example, the Rhind Papyrus offers this in Problem 26: “A quantity whose fourth part is added to it becomes 15. What is the quantity?” In modem notation, we want to solve the equation x + x/4 = 15 for x. The method of false position involves guessing a (probably incorrect) solution, then adjusting it using proportionality. In our problem, the scribe guessed that x = 4, to make the fraction x/4 easier. If x = 4, then x + x/4 = 5. Since we want x + x/4 = 15, we multiply by 3, because 15/5 = 3. If we multiply x= 4 by 3, we get x = 12. You can check that 12 + 12/4 = 15, so we have solved the problem.

Astronomy and the Calendar In ancient Egypt, as in many places at many times, an important use of mathematics was in astronomy. The astronomers of Egypt were priests, which suggests that astronomy was not only a practical science. Astronomers kept track of the Sun, Moon, planets, and stars. One notion they used to track the seasons was that of a helical rising of a star, which meant that the star rose just before the Sun. The most important helical rising was that of Sothus (which we know as Sirius), the brightest star in the sky. This rising occurred in July, shortly before the onset of the Nile floods. Sothus was known as the Dog Star, and we still refer to this time of year as the dog days of summer.

The Egyptians developed the calendar on which ours is based. Their civil calendar, used for official record keeping (as opposed to the everyday lunar calendar), had 365 days, divided into twelve 30-day months, plus an extra five days at the end of the year. Actually, they knew that the year was about days, but they never adjusted their calendar with leap years, as we do.

EXERCISES

1.5 Each of the numbers below is given in sexagesimal form. Translate each into our decimal form.

a) 2

b) 3, 1, 2

c) 1, 2; 6

d) ;1,40

1.6 Translate each of the decimal numbers into sexagesimal form.

a) 2

b) 122

c) 7265

d) .2

e)

1.7

a) Write the fractions 2/5 and 11/12 in sexagesimal form.

b) Use the results of (a) to write 2/5 + 11/12 in sexagesimal form. (Hint: think of how adding decimals works.)

c) Add 2/5 + 11/12 in our usual way, and confirm that you get the same answer.

1.8

a) Write the fraction 1/15 in sexagesimal form.

b) Use (a) to divide 7 by 15, expressing the result in in sexagesimal form.

19

a) Write the fraction 1/30 in sexagesimal form.

b) Use (a) to divide 43 by 30, expressing the result in in sexagesimal form.

1.10 Use Heron’s method to approximate , accurate to eight decimal places. (A calculator may be necessary.) Check your answer by squaring it.

1.11 Solve the Babylonian problem given in the text: “I summed the areas of my two square-sides so that it was 0;21,40. A square-side exceeds the (other) square-side by 0;10.”

1.12

a) Here is another problem from a Babylonian tablet, written around 2000 BCE: “I have added the area and two-thirds the side of my square and it is 0; 35. What is the side of my square?” Translate this into modem notation. The result should be a quadratic equation.

b) Solve the equation. Do you get the same answer as on the tablet? “You take 1. Two-thirds of 1 is 0; 40. Half of this, 0; 20, you multiply by 0; 20 and it, 0; 6,40, you add to 0; 35 and the result 0; 41,40 has 0; 50 as its square root. The 0; 20 which you have multiplied by itself, you subtract from 0; 50, and 0; 30 is the side of the square.”

1.13 Use duplation to calculate 13 times 15.

1.14 Use duplation to calculate 15 times 22.

1.15 Show that the formula (8d/9)² given in the Rhind papyrus for the area of a circle is equivalent to approximating π by 256/81.

1.16

a) Find the volume of a truncated pyramid with lower base 100 feet, upper base 30 feet, and height 69 feet,

b) No existing papyrus gives the volume of a whole (as opposed to truncated) pyramid, but this can easily be derived from the formula above. What is the formula for the volume of a whole pyramid? (Hint: what happens to b as a truncated pyramid gets closer to a whole pyramid?)

1.17 Around the year 1200 CE, the famous mathematician Fibonacci described a method for expressing any fraction as the sum of distinct unit fractions. The method was simple: find the largest unit fraction less than your number. Then subtract it from your number and repeat. For example, consider 41/42. The largest unit fraction less than this is 1/2. Subtracting, we get 41/42 = 1/2 + 20/42. The largest unit fraction less that 20/42 is 1/3. Subtracting, 20/42 = 1/3 + 6/42, so 41/42 = 1/2 + 1/3 + 6/42 = 1/2 + 1/3 + 1/7, and we are done.

a) Express 7/10 as the sum of distinct unit fractions.

b) Express 8/15 are the sum of distinct unit fractions in two different ways.

1.18 Solve by the method of false position: “A quantity whose seventh part is added to it becomes 32. What is the quantity?”

1.19 Solve by the method of false position: “A quantity whose fifth part is subtracted from it becomes 6. What is the quantity?”

1.20 Suppose that a civilization had a system similar to the Babylonian, but based on 5 instead of 60. If they write the first five numbers as A, B, C, D, and E, how would they write these numbers?

a) 23

b) 72

c) .2

d) .24