Mathematics for the liberal arts (2013)
Part I. MATHEMATICS IN HISTORY
Chapter 4. CALCULUS
4.17 Application: Rocket Science
If we know some simple facts, we can estimate some pretty cool things using only basic calculus. For example, we can figure out roughly how high the Space Shuttle flies, knowing only a few facts about the Shuttle. Calculus really is rocket science.
Although the space shuttle no longer flies, when it did, the first part of the ascent was accelerated by the three main engines as well as two solid rocket boosters (which then detached and fell in the ocean).
In the previous section, we learned that integrating an acceleration function will give us the total change in velocity of an object. In the same way, integrating a velocity function gives us the total change in position of an object. So, if we can determine the acceleration function of the Space Shuttle, then determining the height should be a matter of integrating two times, once to get the velocity and again to get the height.
The facts we need to know about the Shuttle are:
• On the launch pad, the mass of the Shuttle is two million kilograms, 2.0 × 106 kg.
• This mass includes 1.18 million kilograms of fuel (1.18 × 106 kg) that will bum up during the first two minutes of flight. (This includes fuel from both the main engines and the solid rocket boosters.)
• The solid rocket boosters produce a total of 23.6 million Newtons of force, or 2.36 × 107 kg m/s2.
• The main engines produce 5.0 million Newtons of force, or 5.0 × 106 kg m/s2.
Newton’s Second Law
Newton’s second law of motion tells us that force is mass times acceleration, or symbolically,
![]()
We are interested in the acceleration generated by the rocket engines, so we solve and substitute the facts that we know:
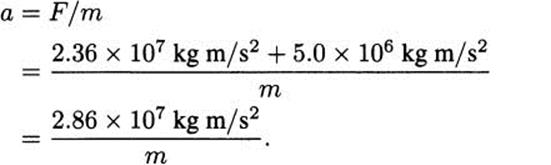
If we knew the mass of the Shuttle, then this calculation would be complete. You may be thinking that we already know that the mass of the Shuttle is 2.0 × 106 kg, but that is not quite correct. The mass certainly starts at two million kilograms, but only two minutes later more than half of the mass has been expended in the form of 1.18 million kilograms of burned fuel. That average rate of fuel use amounts to
![]()
So the mass of the Shuttle is a function of time. We don’t know that the Shuttle uses fuel at a constant rate, but that’s probably not a bad guess. That means that after t seconds, the mass in kilograms is m(t) = 2.0 × 106 – 9833t kg. Using this in the acceleration equation, the acceleration due to the engines is
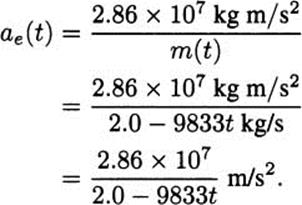
Of course, the engines are not the only acceleration that a rocket experiences. Gravity is also pulling it toward Earth. Fortunately, even for rockets enduring a launch, the acceleration of gravity is easy to compute. It is effectively constant, with the well-known value —9.8 m/s2. Combining this with the acceleration due to the engines, we get the total acceleration on the rocket (as a function of time):
![]()
We should be able to integrate this to get the velocity and height of the rocket.
Velocity of a Rocket
We know that the velocity of the rocket, v(t), will be an antiderivative of a(t), so we integrate:
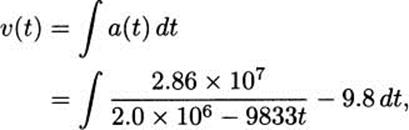
which by the rules of integrals is
![]()
An antiderivative for the second integral is easy to find, since it is the integral of a constant, so let’s focus on the first integral. It is a bit trickier, but not extremely hard.
Let ![]() . Then by the chain rule,
. Then by the chain rule,
![]()
So F is an antiderivative that we can use to compute the integral. Thus
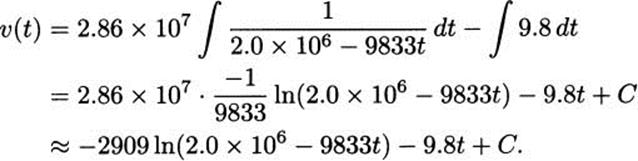
To find the value of C, remember that v(0) = 0 since the rocket starts resting on the launch pad. That means
![]()
and solving, we get C = 2909 1n(2.0 × 106) ≈ 42206. So, our velocity function must be
![]()
To find the velocity after 2 minutes, for example, we compute
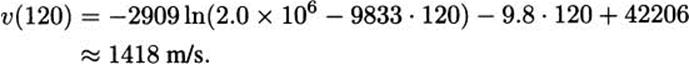
In miles per hour, this is
![]()
Height of a Rocket
We’re only one step away from deriving the height of the rocket. In the last step, we computed that the velocity function of the rocket is
![]()
Since velocity is the derivative of position (the height) we need only integrate one more time. You may quiver at the thought of finding an antiderivative for v(t), but at least some parts of it are easy. The last term is simple:
![]()
And the lines term is too:
![]()
The remaining term is going to take a little more work, but the rules of integrals at least let us factor out the constant in front:
![]()
At its heart, the expression we need to integrate is a logarithm. Alas, we haven’t learned an antiderivative for In t. But this doesn’t mean that no one has, and if you were to consult a table of integrals or use a computer program, you would find that t(In t – 1) is an antiderivative for In t.
We know how to take derivatives, so nothing stops us from checking this for ourselves. Let F(t) = t(ln t – 1). Then by the product rule,
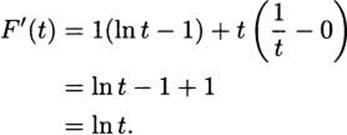
So, we know an antiderivative for In t. Can we build that up to an antiderivative for the expression we need to integrate, namely, ln(2.0 × 106 – 9833t)? If we start from F(t), our antiderivative for In t, we might think to try F(2.0 × 106 – 9833t), and that’s a good guess (though not quite right).
To see that it doesn’t quite work, use the chain rule:
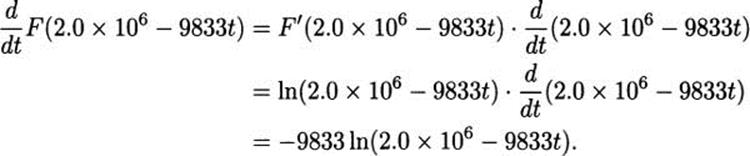
This would be exactly right, except for the extra constant factor of –9833 in front. Hopefully, you see that we can make one last adjustment, dividing by the constant –9833 to get an antiderivative that works perfectly. The antiderivative we need is
![]()
Wow, that was work! But it was work that brings us to our final goal. We can now integrate the velocity to find the position of the rocket at any time t.
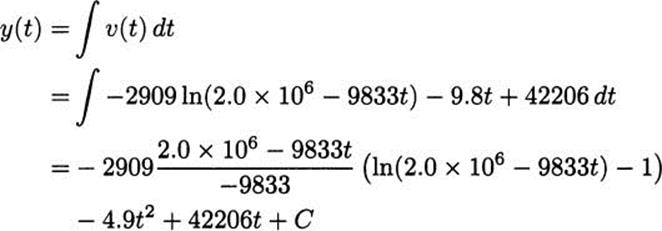
To discover the value of C, simply observe that the rocket begins on the ground. So when t = 0, the height of the rocket is y(0) = 0. It might be best to use a calculator for this part:
![]()
and, solving,
![]()
That makes the height function of the rocket
![]()
To calculate the height of the rocket after two minutes (which is 120 seconds), evaluate y(120) to get approximately 62,000 meters. Is this a reasonable answer?
Let’s convert it to miles:
![]()
If we check our numbers against NASA results, NASA says that after about 2 minutes of flight, the space shuttle has finished its first stage. It is at a height of 28 miles, and it is traveling 3000 mph. We computed a height of 38.5 miles and (in the previous section) a velocity of 3172 mph. It’s not a perfect match, but we are pretty close.
If you feel bad that our conclusion was off by about 10 miles, it may console you to know that at 3000 mph, the space shuttle covers 10 miles in approximately 12 seconds. So don’t think of our calculation as being off by 10 miles. Think of it as being off by 12 seconds.
EXERCISES
4.90 Assume that the space shuttle has a mass of m = 2.0 × 106 kg, and the engines produce F = 2.86 × 107 kg m/s2 of force. For this exercise, imagine that the shuttle stays the same mass, rather than getting lighter as it expends fuel.
a) Use Newton’s second law, F = ma, to compute the acceleration the shuttle feels from the engines.
b) Subtracting gravity, what is the total acceleration the shuttle feels?
c) Knowing that ![]() , what is the velocity of the shuttle when 2 = 120 s?
, what is the velocity of the shuttle when 2 = 120 s?
4.91 Compute the derivative of each function.
a) In t
b) ln(2 – t)
c) ln(2 – 9t)
d) ln(2.0 × 106 – 9833t)
4.92 Compute the derivative of each function.
a) t In t
b) – t + t In t
c) ![]()
d) ![]()
4.93 Consider the height function we derived for the rocket:
![]()
a) Plot the rocket’s height at times 2 = 0, 10, 20, 30, …, 120 s.
b) Find the velocity function of the rocket by computing v(t) = y′(t).