Mathematics for the liberal arts (2013)

Part I. MATHEMATICS IN HISTORY

Chapter 4. CALCULUS

4.18 Infinite Sums

Here’s a mathematical riddle. “I am a real number. I am not negative, but I am less than any positive number. Who am I?”

The answer, of course, is zero. But if we change the setting slightly, it can feel less obvious. For example, perhaps you are acquainted with the infinite repeating decimal number 1.999999… = 1.. Do you know what number this is? As a riddle, we might have said, “I am a real number. I am not greater than 2, but I am greater than any number less than 2. Who am I?” Naturally, the answer is 2. Yet for many people, it feels strange to say “One point nine-repeating is another way of writing the number 2.”

What do we mean when we write a number like 1.999999…? Remember that in our decimal number system, each place in a number has a corresponding value. In this number, the 1 digit is in the ones place. Then a 9 follows in the tenths place, another 9 in the hundredths place and so on. Just as the number 9.81 means 9 + , the expression 1.999999… means

If you think there might be something shifty about adding up infinitely many values, consider that in another context this probably doesn’t upset you at all. You are probably comfortable with the fact that 1/3 = 0.333333… = 0., and 1/7 = . If you think about what those decimal expansions mean, each must refer to an infinite sum.

Geometric Series

An infinite sum is called a series. Our goal is to find the sum of different kinds of series, including the series for 1. and 0.. As a step toward that goal, consider this version of Zeno’s famous dichotomy paradox: Imagine yourself standing on the number line. You are at the number 0 and facing towards the 1. Now step half the distance to 1. This puts you on 1/2. Step half the distance again, to 3/4. Step half the distance again, and again, and so on, forever. Where do you end up?

Hopefully, you see that, in the language of our riddle, you end up at a real number no larger than 1 but beyond any of the numbers less than 1. That is, you are at the number 1. As a series, this conclusion could be written as

To be very careful about this, however, consider where you are after each step. After your first step (of size 1/2), your distance from 1 was also 1/2. After your second step, (of size 1/4 = 1/2²), you were at 3/4 and your distance from 1 was only 1/4 = 1/2². Each step is half as large as the previous, so the nth step is of size l/2ⁿ and it leaves you short of 1 by a distance of only l/2ⁿ. As n becomes larger and larger, you get closer and closer to 1 (though you never reach it in any finite number of steps). In the language of calculus, we solve the riddle by taking a limit, and here the limit is 1.

Mathematically, the sum of a series is always defined this way. We add up a finite (but ever growing) number of terms, then see if the finite sums approach some limit. If they do, the series is said to be convergent, and the limit is called the sum of the series.

The series , and 1. are all members of an important family of (convergent) series, the geometric series. A geometric series is a series of the form

The Zeno series corresponds to a = 1/2 and r = 1/2. The value 0. corresponds to a = 3/10 and r = 1/10. The value 1. is not a geometric series, but the decimal part, 0., is a geometric series with a = 9/10 and r = 1/10.

Since the sum of a series comes from taking a limit of finite sums, it is important to be able to compute finite sums. For the geometric series, the finite sums are given by a well known formula.

Geometric Sum Formula. For real numbers a, r where r ≠ 1,

There are two typical ways to derive this fact. If you are comfortable with polynomial long division, then computing is a matter of dividing rⁿ – 1 by r – 1. Otherwise, this formula can be checked by computing the product

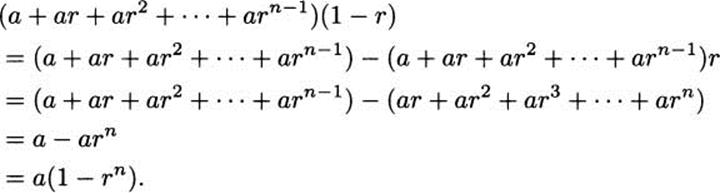
Since , we can divide both sides by (1 – r) to get the finite sum formula.

Now that we know how to add finite geometric sums, we can ask what happens when n approaches infinity. The most interesting case is when |r| < 1, since in that case rⁿ gets closer and closer to 0. To see this, consider any number of size (absolute value) less than 1. If you square your number and cube it, and so on, it becomes smaller and smaller.

Since rⁿ → 0, we now know the limit of a geometric series.

Geometric Series Formula. For real numbers a, r, with |r| < 1,

EXAMPLE 4.47

The Zeno series is a geometric series with a = 1/2 and r = 1/2. The sum of the series, therefore, is

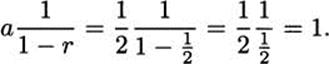
EXAMPLE 4.48

The value 0. represents a geometric series with a = 3/10 and r = 1/10. The sum is therefore

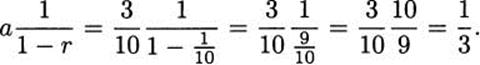
EXAMPLE 4.49

The value 1. is not a geometric series, but 0. is. Here a = 9/10 and r = 1/10. The sum of the series part is

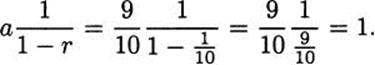
And finally, the value is 1. = 1 + 0. = 1 + 1 = 2.

EXAMPLE 4.50

What value does x = 0. = 0.13131313… represent?

Solution: This question is slightly harder, but one way to write this as a series is

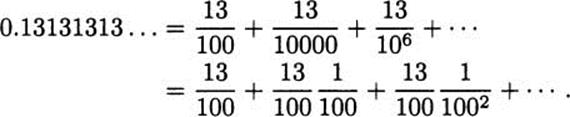
This is a geometric series with and . The sum is

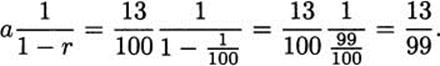
Here’s another approach, using algebra. Let x = 0.. Our job is to find x. Notice that lOOx = 13.131313… = 13.. Now compute:

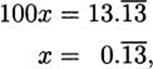
and subtracting.

Solving, we see again that x = 13/99.

The Harmonic Series

Are there series that don’t converge? Of course. The simple series 1 + 1 + 1 + o o o fails to converge. Rather than getting close to any fixed number, it becomes larger and larger as you take more terms. Such a series is called divergent. In this example, we say that the series “diverges to infinity.”

It is fairly clear that if the terms of a series don’t get smaller and smaller, the series will be divergent. But what if the terms do get smaller? Is that enough to make the series converge? As it turns out, there are divergent series whose individual terms get smaller and smaller. The most famous is the harmonic series.

Definition. The harmonic series is the sum

As always, the key to understanding the limit of any series is to look at n terms, and then see what happens as n gets larger and larger. If we take the first n terms of the harmonic series, we get .

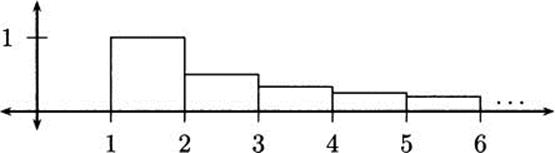
To see how big this sum is, we’ll use a geometric argument. Draw rectangles having area , and stack them next to each other on the number line, starting at the value x = 1, as indicated by the five rectangles in Figure 4.38. The jth rectangle should have width 1 and height , so that each area is the jth term of the harmonic series.

Figure 4.38 The harmonic series as areas of rectangles.

Now that we are thinking of this sum as an area, our knowledge of calculus and integrals can be applied. Notice what happens if we insert the curve y = l/x into the picture, as in Figure 4.39.

Figure 4.39 Harmonic series compared with y = l/x.

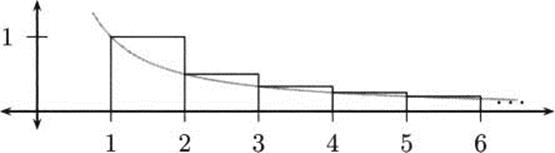
Look first at what happens on the interval [1,2]. On this interval, we know that y = l/x will never be larger that 1. So, the area of the rectangle is larger than the area under the curve. In the language of integrals, we can write

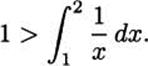
The same thing happens in the next interval. In [2,3], we know that y = 1/x will never be larger than , which is precisely the height of the second rectangle. So the area under the curve is smaller than the area of the rectangle. If we combine this with what we know about the first rectangle, we find that the sum of the first two rectangles is more than the area under the curve over the interval [1,3]:

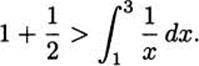
We can continue in the same way. The area of five rectangles is greater than the area under the curve over the interval [1,6]. In general, the area of n rectangles will be greater than the area under y = 1/x over the interval [1, n + 1]. Written out,

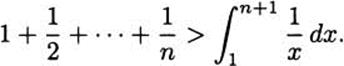
Here’s the point. We know how to compute the area under the curve, because we know how to do integrals. All we need is an antiderivative for f(x) = 1/x, and F(x) = In x works fine. Applying the Fundamental Theorem of Calculus,

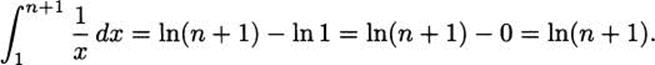
What does this tell us about the harmonic series? If we take n terms and add them together, it is true that we don’t know exactly what the result will be. But we do know that whatever that sum is, it will be more than ln(n + 1). Since ln(n + 1) goes to infinity as n gets larger, the harmonic series must also go to infinity as n grows.

Theorem. The harmonic series diverges. That is,

EXERCISES

4.94 Let x = 0.24 = 0.24999….

a) Write x as a fraction.

b) What other decimal expression represents x?

4.95 Write 2. = 2.222… as a fraction.

4.96 Write 0. = 0.123123123… as a fraction in lowest terms.

4.97 Interpret this math joke.

An infinite number of mathematicians walk into a bar. The first mathematician says to the bartender, “I’d like 1 glass of beer.” The second mathematician says, “I’d like 1/2 glass of beer.” The third mathematician says, “I’d like 1/4 glass of beer.” At that point, the bartender gets annoyed, slams a couple of mugs on the bar, and says, “Look. Here’s two glasses of beer. Now you all get out of here!”

a) Why does this joke work?

b) When one of the authors told this joke to a group of advanced students, a student remarked, “It’s a good thing the third mathematician didn’t ask for 1/3 of a glass!” Why did that get a laugh from the other students?