Mathematics for the liberal arts (2013)

Part II. TWO PILLARS OF MATHEMATICS

Chapter 5. NUMBER THEORY

5.3 Irrational Numbers

The Problem

Mathematicians have long struggled with the question of what a number is. Early civilizations mostly accepted positive integers and fractions; zero and negative numbers took much longer to gain acceptance as full-fledged numbers.

One place where numbers can be found is in measuring lengths. Which numbers appear as lengths? It is not hard to show that every positive integer and fraction can be represented as a length. To many people, it seems self-evident that these are the only lengths. Roughly 2500 years ago it was discovered that this is not the case.

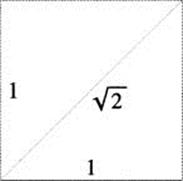
The length that led to this discovery is not obscure: it is the length of the diagonal of a square of side 1 (Figure 5.1). Using the Pythagorean Theorem, this length is .

Figure 5.1 as a length.

The Theorem

There are no integers a and b such that = a/b.

Proof. We will give a proof by contradiction. We will assume that the theorem is false, and show that this leads to a logical contradiction.

So let us assume that integers a and b exist such that = a/b. Recall that we can reduce any fraction to one in lowest terms by dividing numerator and denominator by any common factors. Let us assume that we have done that, so that a and b don’t have any common factors.

Now square the above equation to get 2 = (a/b)². Multiplying both sides of this equation by b² gives

This means that a² is even—divisible by 2. We saw in the last section that the product of two odd numbers is always odd, so a cannot be odd, i.e., a is divisible by 2. Hence a = 2c for some integer c. Substituting this into the above equation, we get 2b² = (2c)² = 4c². Hence b² = 2c². Therefore, b² is even, so b is also divisible by 2. We have arrived at our contradiction: both a and b are divisible by 2, contradicting the assumption that a and b have no common divisors. Therefore, there do not exist integers a and b such that = a/b.

Numbers that can be expressed as ratios of two integers are called rational numbers. Ones that cannot be so expressed are irrational. So the theorem tells us that is irrational. Much later, in the 19th century, it was shown that, in some sense, most lengths are irrational. But when the first irrational number was found, it no doubt caused much consternation. The discovery was made by the Pythagoreans, in the 5th or 6th century BCE. Like many of the greatest discoveries in science, it was negative; something was shown to be impossible.

This theorem also implies a result in geometry concerning commensurable line segments. Two line segments are commensurable if there is a third line segment that can fit into each of the two a whole number of times. For example, line segments of length 1/2 and 1/3 are commensurable, because a line segment of length 1/6 fits into the one of length 1/2 exactly three times and into the one of length 1/3 exactly twice. Early on, many mathematicians thought that all pairs of line segments were commensurable. This idea was often used in geometric proofs. But it turned out to be wrong.

Corollary. The side of a unit square and its diagonal are not commensurable.

A corollary is a theorem that follows easily from another theorem. So let us see how this follows from the last theorem.

Again, we proceed by contradiction. Suppose that the side and diagonal of a unit square are commensurable, that we have a line segment of length x that can fit into each of them an integral number of times. Suppose that it fits into the diagonal a times, and into the side b times. Then we have ax = and bx = 1. Dividing the two equations yields a/b = , which we know to be impossible for integers a and b. So our two line segments must be incommensurable.

EXERCISES

5.7 Which of the following do you think are rational numbers?

a)

b)

c) 117/3459753

d) π(Hint: the Internet is a great resource.)

5.8 True of false? A number is rational if, and only if, its decimal expansion terminates. (Recall that the decimal expansion of 1/4, for example, is .25.)

5.9 Prove that is irrational.

5.10 Prove that + 10 is irrational.

5.11 Prove that if r and s are rational numbers, then r + s, r – s, and rs are rational numbers, and if s ≠ 0, then r/s is a rational number.

5.12 One of the authors had an idea when he was very young. He was measuring a length with a ruler. The ruler had marks every inch, half-inch, and quarter-inch. The length didn’t quite match one of the marks, so he had to mentally create another mark at an eighth-inch place. This worked, and gave him his idea. If it didn’t work, then he could go to sixteenths of an inch, thirty-seconds of an inch, then sixty-fourths, etc., until he got an exact match.

a) What is wrong with this idea?

b) What numbers can be exactly measured in this way?

5.13 Look up the origin of the word corollary. How does it relate to a little theorem presented after a big theorem?