Mathematics for the liberal arts (2013)

Part II. TWO PILLARS OF MATHEMATICS

Chapter 5. NUMBER THEORY

5.6 Relatively Prime Integers

Bézout’s Identity

We begin this section with a result that turns out to be remarkably useful.

Bézout’s Identity. Let a and b be integers, not both 0. Then there are integers u and v such that gcd(a, b) = au + bv.

As an example, let a = 144, b = 22. You can check that gcd(144,22) = 2. In this case, we can choose u = 2 and v = – 13. They satisfy Bézout’s Identity, since 2 = 144 · 2 + 22 · (– 13). (If you don’t see where u and v came from, it is because we just pulled them out of a hat. We will see later how one can find them.)

Bézout’s Identity was named after a French mathematician, Étienne Bézout (1730–1783), although the result was already known to Claude Gaspard Bachet de Méziriac (1581–1638) more than a century earlier. Bézout actually proved a generalization of it.

We first apply Bézout’s Identity to proving a nice theorem about common divisors.

The common divisors of a and b are the divisors of gcd(a, b).

Proof. Let gcd(a, b) = d. First we show that every common divisor of a and b divides d. Let c be a divisor of a and b. Using Bézout, we can write d = au + bv, for some integers u and v. Now we use our properties of divisibility. Since c | a, we have c | au. Since c | b, we have c | bv. Since c | au and c | bv, we have c | (au + bv). So c | d.

The other half is pretty easy to prove. Let e be a divisor of d, say d = er. Now d divides a and b, so we can write a = ds and b = dt for some integers s and t. Then a = ds = (er)s = e(rs) and b = dt = (er)t = e(st), so we have e dividing both a and b, which is what we needed to show.

Think about this. We have just reduced the problem of finding the common divisors of two integers to finding the divisors of one integer. Now that’s progress.

EXAMPLE 5.13

Find the common divisors of 84 and 192.

Solution: First we use the Euclidean Algorithm to find gcd(192,84).

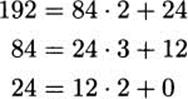
So gcd(192,84) = 12. By the theorem, the common divisors of 84 and 192 are the divisors of 12, namely, ±1, ±2, ±3, ±4, ±6, ±12.

Relatively Prime Integers

Consider the following two statements.

i. If a | bc and a b, then a | c.

ii. If a | c and b | c, then ab | c.

They may seem reasonable, but are they always true? Unfortunately, no. Here are counterexamples.

i. Let a = 6, b = 9, c = 8. Then a | bc and a b, but a c.

ii. Let a = 15, b = 5, c = 60. Then a | c and b | c, but ab c.

Is that the end of the story? No, if we are careful, we can find somewhat more restricted statements similar to the ones above, that are true. To formulate these, we need a new notion.

Definition. Let a and b be integers. We say that a and b are relatively prime, or coprime, if gcd(a, b) = 1. In other words, relatively prime integers are those whose common divisors are only 1 and – 1.

EXAMPLE 5.14

(a) 12 and 5 are relatively prime, since gcd(12,5) = 1.

(b) 27 and 96 are not relatively prime, since 3 divides both 27 and 96.

The next two results are versions of the two statements with which we started this section.

Let a divide bc, and a and b be relatively prime. Then a divides c.

Proof. Since gcd(a, b) = 1, Bézout lets us write 1 = au + bv for some integers u and v. Multiply this equation by c to get c = acu + bcv. Now look at the right-hand side of this new equation. Certainly a | acu. Also, since a | bc, we have a | bcv. Since a divides both terms on the right, it must divide the whole thing. Hence a | c.

Suppose that integers a and b both divide c, and that a and b are relatively prime. Then ab divides c.

Proof. Since a | c, there is some integer s such that c = as. Since b | c, there is some integer t such that c = bt. Since gcd(a, b) = 1, we have integers u and v such that 1 = au + bv. Multiply the last equation by c to get c = acu + bcv.Now plug in c = bt for the first c, and c = as for the second:

Thus c is a multiple of ab, so ab | c.

EXAMPLE 5.15

(a) Does 7 divide 710,000? No. Apply the first result, with a = 7, b = 10,000, and c = 71. Because 10,000 = 10⁴ = 2⁴ · 5⁴, we can see that 7 and 10,000 have no factors in common, so 7 and 10,000 are relatively prime, i.e., gcd(7,10,000) = 1. Therefore, if 7 were to divide 710,000, the theorem would tell us that 7 divides 71, which it does not.

(b) Suppose that a number x is even and is divisible by 5. Then it is divisible by 10. This is true by the second result, with a = 2, b = 5, and c = x.

Computing Bézout

How do we find the integers u and v of Bézout’s Identity? It is possible using the Euclidean Algorithm!

Let’s do an example, with a = 69 and b = 31. We will start by running the Euclidean Algorithm.

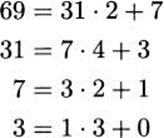
So gcd(69,31) = 1. Now we will find u and v such that 69u + 31v = 1.

The method we use will express each of the remainders r_i above, that is, each of 7, 3, and 1, in the form r_i = 69x_i + 31y_i.

Starting with the first equation 69 = 31 · 2 + 7, we can write

Then using this and 31 = 7 · 4 + 3, we have

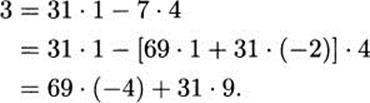
Finally, from 7 = 3 · 2 + 1 we have

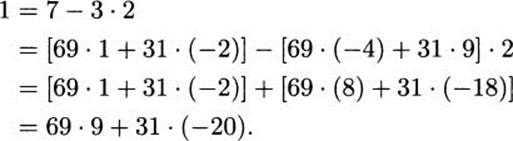
Thus u = 9 and v = –20 work.

EXERCISES

5.29 Find u and v such that 7u + 3v = gcd(7,3).

5.30 Find u and v such that 84u + 351v = gcd(84,351).

5.31 Find the common divisors of 84 and 351.

5.32 Does 11 divide 23,000?

5.33 Consider the set of all numbers of the form 6u + 8v. We know from Bézout that 2, the gcd of 6 and 8, is in this set. What else is in the set? (Try some values of u and v, and look for a pattern.)

5.34 Repeat the last problem for the set of all numbers of the form 9u + 12v.

5.35 Repeat the last problem for the set of all numbers of the form au + bv, where a and b are any integers.