Mathematics for the liberal arts (2013)

Part II. TWO PILLARS OF MATHEMATICS

Chapter 5. NUMBER THEORY

5.7 Mersenne and Fermat Primes

One of the oldest problems in number theory is to find primes. Is there a formula for primes? Or, failing that, is there a formula for some of the primes?

Mersenne Primes

Consider numbers of the form 2^p – 1, where p is prime. The first few numbers of this form are

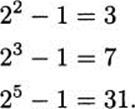
Note that 3, 7, and 31 are all primes. When a number of the form 2^p – 1 is a prime, it is called a Mersenne prime. (Mersenne was a 17th century mathematician who studied such primes.) Could this then be a formula for obtaining primes? Unfortunately no, since not all numbers of this form are in fact primes. (See the exercises.)

Still, some numbers of this form are prime, and some are still being discovered. In 1996 the Great Internet Mersenne Prime Search (GIMPS) was launched (see http://www.mersenne.org/prime.htm). This is a distributed computing project, a collaborative project in which thousands of users around the world run free software as “screen savers” during their computers’ idle time. Since its start, this project has steadily, albeit slowly, been finding monster primes. The biggest at the time of this writing is 2^43112609 – 1, found in 2008. It has 12,978,189 digits.

Euclid knew about primes of this type, but they are named after a French friar, Marin Mersenne (1588–1648), who checked the primality of all the numbers of the form 2^p – 1, up to p = 257. He was actually mistaken in five cases. It isn’t known whether there are infinitely many Mersenne primes.

Mersenne primes have a strong connection with perfect numbers. A positive integer n is a perfect number if it is the sum of all its divisors, excluding n itself. For example, 6 is a perfect number, since 6 = 1 + 2 + 3. Another example is 28, since 28 = 1 + 2 + 4 + 7+14. Mathematicians have been interested in finding perfect numbers since the ancient Greeks. Perfect numbers are rare; the next one after 28 is 496. Euclid proved that if 2^p – 1 is a Mersenne prime, then 2^{p – 1}(2^p – 1) is a perfect number. So, for example, if p = 3, the Mersenne prime is 2³ – 1 = 7, and 2^{3 – 1}(2³ – 1) = 28 is perfect. Conversely, Leonhard Euler in the 18th century proved that every even perfect number is of the form 2^{p – 1}(2^p – 1), where 2^p – 1 is a Mersenne prime. What about odd perfect numbers? Nobody knows. No one has found one, but nobody has proven that they don’t exist.

Fermat Primes

Another attempt to find a formula for primes was initiated by the great Pierre de Fermat in the 17th century. He noticed that all these numbers are prime.

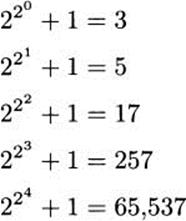
This led him to conjecture, in 1650, that all numbers of the form 2²_k + 1 were prime. Primes of this form are called Fermat primes.

Fermat primes have a surprising connection to a very old problem, a connection discovered by Carl Friedrich Gauss some 150 years or so after Fermat.

The problem is from the ancient Greek mathematicians. They were interested in which plane figures could be drawn using only a straightedge (to make straight lines) and a compass (to make circles). The question that Gauss answered was this: for which values of n can one construct a regular n-gon, using only compass and straightedge? (A regular n-g on is a symmetric polygon with n sides, for example, an equilateral triangle or a square.) The answer is that a regular n-g on can be so constructed if and only if n is either a power of 2 or n = 2^mp₁p₂ … p_r, where m ≥ 0 and p₁, p₂,…, p_r are distinct Fermat primes.

How has Fermat’s conjecture fared? He showed that 2^2k + 1 is prime for k = 0, 1, 2, 3, 4. He tried to prove that 2^2k + 1 is always prime, but failed. The reason for his failure was discovered by Leonhard Euler in 1732: 2²⁵ + 1 = 4,294,967,297 is not prime. Some dozens of other cases have been settled. As for Mersenne primes, there also is a distributed computing project aimed at Fermat primes. So far, the only primes of this form are the ones that Fermat knew.

Nobody yet has been able to find a formula that generates an infinite number of primes and no composite numbers.

EXERCISES

5.36 Find the first five Mersenne primes and their associated perfect numbers.

5.37 What is the first number of the form 2^{p – 1}, with p a prime, that is not a prime?

5.38 Use Euclid’s theorem on perfect numbers to find a perfect number with four digits.

5.39 What is the biggest Mersenne prime known? (Check GIMPS.)

5.40 What is the largest prime of any type currently known? (See, for example, http://primes.utm.edu/.)

5.41 Show that 641|(2²⁵ + 1).

5.42 Has anyone found a Fermat prime that Fermat didn’t already know? (Check the Web.)

5.43 Is a regular 100-gon constructible using only straightedge and compass? What about a regular 101-gon? A regular 102-gon?